Слайд 2
Метод анализа иерархий (МАИ) разработан американским математиком
Томасом Саати. Представляет собой математический инструмент системного подхода к
сложным проблемам принятия решений, позволяет комплексно подойти к оценке конкурентоспособности товара, услуги предприятия.
Метод анализа иерархий широко применяется в сфере управления качеством и конкурентоспособностью и читается в рамках многих специализированных программ, таких как Six Sigma, Lean Six Sigma, и QFD.
Слайд 3
Шесть сигм (англ. six sigma) — концепция управления
производством, разработанная в корпорации Motorola в 1980-е годы и
популяризированная в середине 1990-х после применения её как ключевой стратегии в General Electric.
Суть концепции сводится к необходимости улучшения качества выходов каждого из процессов, минимизации дефектов и статистических отклонений в операционной деятельности.
Концепция использует методы управления качеством, в том числе, статистические методы, требует использования измеримых целей и результатов, а также предполагает создание специальных рабочих групп на предприятии, осуществляющих проекты по устранению проблем и совершенствованию процессов («чёрные пояса», «зелёные пояса»).
Слайд 4
Методика «шести сигм» имеет несколько отличительных черт от
предыдущих методик управления качеством:
результаты каждого проекта должны быть измеряемыми
и выражаться в количественном отношении;
высшее руководство в большей степени рассматривается как сильный и харизматичный лидер, на которого можно положиться;
создание специальной системы присвоения званий специалистам методики по аналогии с восточными единоборствами — «чемпион», «чёрный пояс», что ведёт к лучшему усвоению концепции среди работников;
принятие решений только на основе поддающейся проверке информации, без допущений и предположений.
Слайд 5
Многие соискатели научных степеней выбирают МАИ в качестве
объекта научных и диссертационных исследований.
Раз в два года
проводится Международный симпозиум, посвященный МАИ (International Symposium on Analytic Hierarchy Process, ISAHP), на котором встречаются как ученые, так и практики, работающие с МАИ.
Слайд 6
МАИ
Особенность метода заключается в том, что он позволяет
в интерактивном режиме найти вариант (альтернативу), который наилучшим образом
согласуется с пониманием сути проблемы и требованиями к ее решению.
Слайд 7
Оценку конкурентоспособности товара (услуги,
предприятия) необходимо начинать с построения иерархической структуры, которая включает
цель, критерии, альтернативы и другие рассматриваемые факторы, влияющие на выбор.
Метод анализа иерархий содержит процедуру синтеза приоритетов, вычисляемых на основе субъективных суждений экспертов. Число суждений может измеряться десятками или даже сотнями. Математические вычисления для задач небольшой размерности можно выполнить вручную или с помощью калькулятора.
Слайд 8
Порядок применения Метода Анализа Иерархий
Слайд 9
Построение иерархической структуры, объединяющей цель выбора, критерии, альтернативы
и другие факторы, влияющие на выбор решения, помогает проанализировать
все аспекты конкурентоспособности и глубже вникнуть в суть задачи.
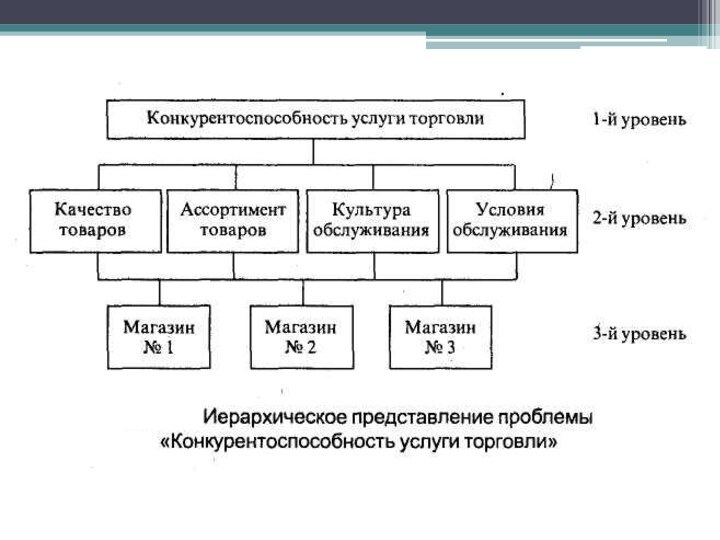
Иерархическая структура — это графическое представление проблемы конкурентоспособности в виде перевернутого дерева, где каждый элемент, за исключением самого верхнего, зависит от одного или более выше расположенных элементов. В теории конкурентоспособности на самом верхнем уровне находится конкурентоспособность товара, услуги или предприятия; элементы нижнего уровня представляют множество вариантов достижения цели (альтернатив); элементы промежуточных уровней соответствуют критериям или факторам, которые связывают цель с альтернативами
Слайд 10
Шаблон иерархической структуры оценки конкурентоспособсности
Слайд 11
Существуют специальные термины для описания иерархической структуры МАИ.
Каждый уровень состоит из узлов. Элементы, исходящие из узла,
принято называть его детьми (дочерними элементами).
Элементы, из которых исходит узел, называются родительскими.
Группы элементов, имеющие один и тот же родительский элемент, называются группами сравнения.
Родительские элементы Альтернатив, как правило, исходящие из различных групп сравнения, называются покрывающими Критериями.
Слайд 12
Используя эти термины для описания рисунка , можно
сказать, что четыре Критерия — это дети Цели; в
свою очередь, Цель — это родительский элемент для любого из Критериев.
Каждая Альтернатива — это дочерний элемент каждого из включающих ее Критериев. Всего на диаграмме присутствует две группы сравнения: группа, состоящая из четырех Критериев и группа, включающая три Альтернативы.
Слайд 13
Оценка конкурентоспособности услуги торговли на основе МАИ.
Слайд 14
На первом этапе проблема представляется в виде разноуровневой
иерархии, на вершине которой (1-й уровень иерархии) показывается цель
исследования,
в рассматриваемом примере, — конкурентоспособность магазина
Слайд 16
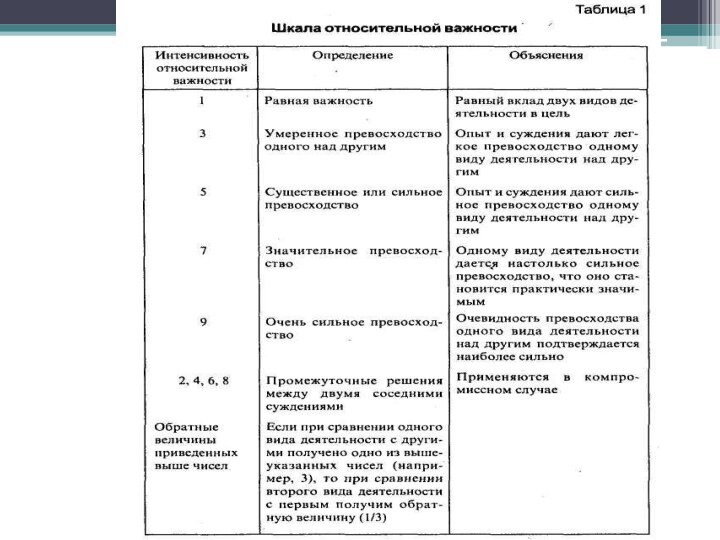
На втором этапе составляется матрица попарных сравнений (на
основе шкалы в табл. 1) для 2-го уровня (табл.
2) — критериев конкурентоспособности с целью установления относительной важности (коэффициента весомости) каждого критерия.
Слайд 18
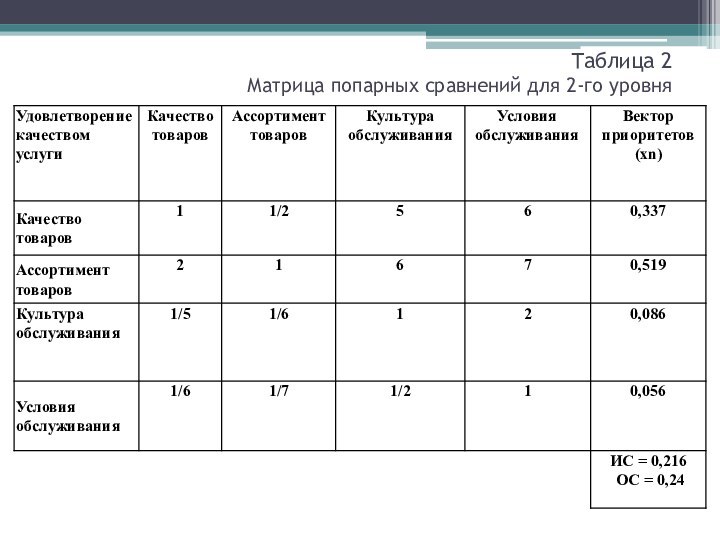
Таблица 2
Матрица попарных сравнений для 2-го
уровня
Слайд 19
Эксперты обсуждают и сравнивают с помощью шкалы относительной
важности относительную важность элементов матрицы с элементами наверху.
Иными
словами, производится попарное сравнение критериев конкурентоспособности между собой. Так, если элемент слева (допустим, ассортимент) несколько превосходит по важности элемент наверху (допустим, качество), то в клетку заносится положительное число (в нашем случае — число 2).
Слайд 20
В клетку, симметричную относительно диагонали, автоматически заносится обратное
число (дробь 1/2). Далее, поскольку критерий «Культура обслуживания» более
существенно уступает критерию «Качество», то в симметричных клетках проставляются числа 5 и 1/5 и т.д.
Слайд 21
После того как проблема иерархически воспроизведена (структурирована) и
проставлены результаты субъективных парных суждений экспертов, производится расчет «локальных»
приоритетов — векторов2 приоритетов (вектором называется участок матрицы из одной строки или столбца), которые выражают относительное влияние элемента (критерия) на элемент более высокого уровня — конкурентоспособность.
Слайд 22
Значения векторов приоритетов рассчитывают следующим образом.
1. Перемножают числа
в каждой строке и из произведения извлекают корень п-й
степени (в нашем случае 4-й степени, исходя из четырех критериев):
Слайд 23
2.Находят сумму компонент:
3.Производят нормализацию полученных значений по формулам:
Слайд 24
4. Полученные величины х1, x2, х3, х4 являются
значениями векторов приоритетов. Значение критерия с наивысшим приоритетом (критерия
«Ассортимент») — 0,519.
Параллельно с расчетом локальных приоритетов производится обработка полученных данных методами математической статистики, в частности расчет «индекса согласованности» (ИС) и «отношения согласованности» (ОС). Если значение ОС выходит из заданных пределов, то делается вывод о несогласованности мнений экспертов и необходимости повторного обсуждения относительной важности критериев конкурентоспособности.
Слайд 25
На третьем этапе составляются матрицы попарных сравнений для
3-го уровня, т.е. применительно к магазинам, или,
по терминологии МАИ,
строятся «матрицы парных сравнений на 3-м уровне по отношению к критериям 2-го уровня» (табл. 3).
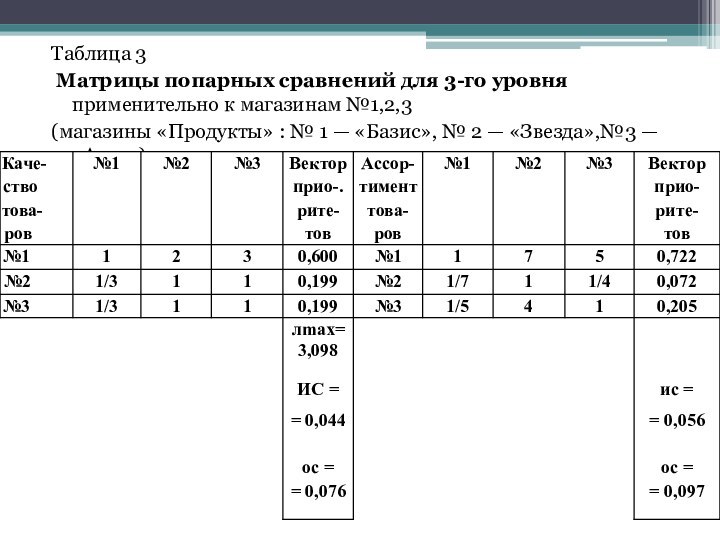
Исходными данными для таблицы были значения комплексных показателей ассортимента, качества, культуры обслуживания магазинов «Продукты» (см. табл. 23).
Слайд 26
Таблица 3
Матрицы попарных сравнений для 3-го уровня
применительно к магазинам №1,2,3
(магазины «Продукты» : № 1 —
«Базис», № 2 — «Звезда»,№3 — «Аист»)
Слайд 27
На четвертом этапе реализуется «принцип синтеза»: локальные приоритеты
настоящего уровня (в нашем случае — приоритеты магазинов) умножают
на приоритет соответствующего критерия на вышестоящем уровне (в нашем случае — весомость критерия конкурентоспособности):
№ 1: 0,6 х 0,337 + 0,722 х 0,519 + 0,151 х 0,086 + 0,674 х 0,056 = 0,604; № 2: 0,199 х 0,337 + 0,072 х 0,519 + 0,63 х 0,086 + 0,1 х 0,056 = 0,186; № 3: 0,199 х 0,337 + 0,205 х 0,519 + 0,218 х 0,086 + 0,225 х 0,056 = 0,201.
Слайд 28
В результате получают значения обобщенных или глобальных приоритетов
— обобщенные критерии конкурентоспособности (табл. 4).
Таблица 4
Синтезирование локальных приоритетов
Таблица
4
Синтезирование локальных приоритетов
Таблица 4
Синтезирование локальных приоритетов
Слайд 29
Из таблицы видно, что наибольшую конкурентоспособность (без учета
стоимости реализуемых продуктов) имеет магазин № 1 «Базис».
Сравнение результатов
оценки методами среднего взвешенного арифметического и МАИ показывает большую амплитуду колебаний значений конкурентоспособности, рассчитанной по второму методу.
Это объясняется тем, что при расчете методом МАИ был применен метод среднего геометрического для определения коэффициента весомости («вектора приоритета»).