Слайд 2
2.1. Представление количественных данных
Количественные данные для анализа и
интерпретации необходимо обобщить.
Первый этап представления – это упорядочивание
данных по величине от максимальной до минимальной.
Такое представление называют несгруппированным рядом.
Слайд 3
Пример: Группа детей шестилетнего возраста была протестирована по
методике Керна-Йерасика (тест на школьную зрелость). Результаты тестирования занесены
в таблицу 1
Оценки проставлялись в алфавитном порядке так, как записаны дети.
Слайд 4
Упорядочим ряд данных по убыванию:
15, 14, 14, 14,
14, 13, 13, 13, 13, 13, 13, 13, 13,
12, 12, 9
Получим несгруппированный ряд данных.
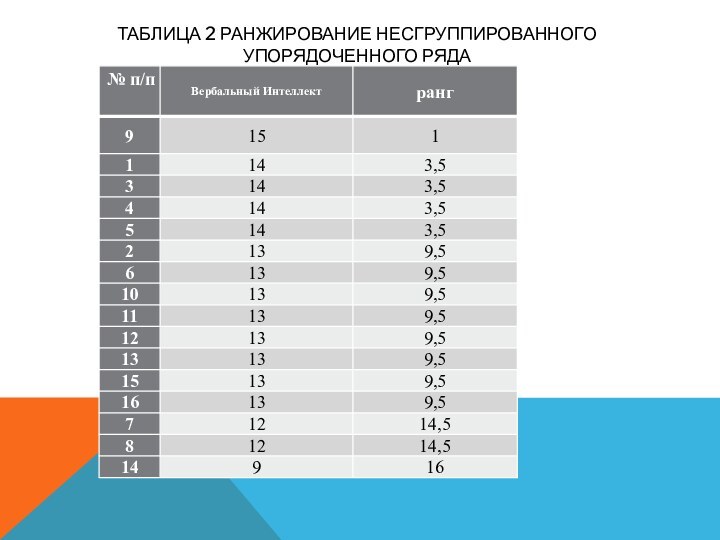
Проранжируем полученные данные эти данные, присваивая 1 ранг наибольшему значению.
число 15 будет иметь ранг - 1;
14 принадлежит 4 ранга – 2, 3, 4 и 5.
Общий ранг вычисляем следующим образом:
(2+3+4+5)/4=3,5
т.е. складываем все ранги и делим на число повторений.
ранг числа 13 - ?
ранг числа 12 - ?
и числа 9 - ?
Слайд 5
Таблица 2 Ранжирование несгруппированного упорядоченного ряда
Слайд 6
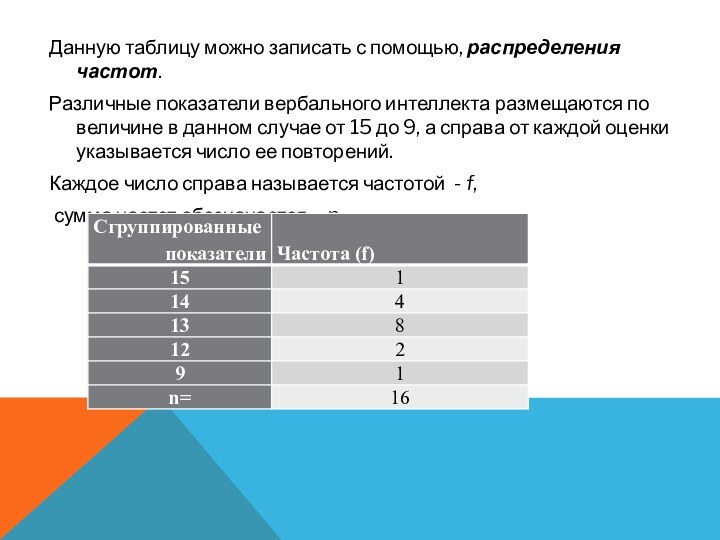
Данную таблицу можно записать с помощью, распределения частот.
Различные показатели вербального интеллекта размещаются по величине в данном
случае от 15 до 9, а справа от каждой оценки указывается число ее повторений.
Каждое число справа называется частотой - f,
сумма частот обозначается - n.
Слайд 7
2.2. Числовые характеристики распределения данных
Частотное распределение ничего не
говорит о статистических закономерностях, которые описывали бы числовые характеристики
изучаемой совокупности.
К характеристикам распределения, описывающим количественно его структуру и строение, относятся:
• характеристики положения;
• рассеивания;
• асимметрии и эксцесса.
Слайд 8
Характеристики положения (центральной тенденции):
мода (Мо),
медиана (Ме)
квантили
среднее арифметическое (M ).
Слайд 9
Определение: величина признака, которая встречается чаще всего в
изучаемом
ряду, или совокупности называется модой (Мо).
В дискретном ряду
Мо определяется без вычисления, как значение признака с наибольшей частотой
Мо= ?
Слайд 10
Пример: найти моду ряда
12, 13, 14, 14, 14,
16, 16, 16, 18, 19
12, 13, 14, 14, 14,
16, 16, 18, 18, 18 19
12, 12, 12, 14, 14, 14
Слайд 11
Два значения признака, стоящие рядом, встречаются одинаково часто.
мода равна среднему арифметическому этих двух значений
2. Два
значения, встречаются также одинаково часто, но не стоят рядом.
ряд данных имеет две моды, т.е. он бимодальный.
3. Если все значения данных встречаются одинаково часто
ряд не имеет моды.
Если в ряду данных встречается два или более равных значений признака, то говорят о неоднородности совокупности.
Слайд 12
Определение: медианой (Ме) – называется такое значение признака,
которое делит ряд пополам.
При нечетном числе элементов в
ряду данных, медиана равна центральному члену ряда,
При четном среднему арифметическому двух центральных значений ряда.
Ме= ?
Вычисление медианы имеет смысл только для порядкового признака.
Слайд 14
Квантиль – это такое значение признака, которое делит
распределение в заданной пропорции:
слева 0,5%, справа 99,5%;
слева
2,5%, справа 97,5% и т.п.
Слайд 15
Разновидности квантилей:
1) Квартили Q1, Q 2, Q3 –
они делят распределение на четыре части по 25% в
каждой;
2) Квинтили К1, К2, К3, К4 – они делят распределение на пять частей по 20% в каждой;
3) Децили D1, ...,D9, их девять, и они делят распределение на десять частей по 10% в каждой;
4) Процентили P1, Р2 ...,Р99, их девяносто девять, и они делят распределение на сто частей по 1% в каждой части.
Слайд 16
Характеристики рассеивания
Изучается средний возраст в двух группах, состоящих
каждая из 6-ти человек. Значения признака распределились следующим образом:
1
группа – 10, 10, 10, 50, 50, 50 М1= 30
2 группа – 30, 30, 30, 30, 30, 30 М2=30
Ошибка произошла из-за разброса значений возраста в этих группах.
Слайд 17
Существует несколько способов оценки степени разброса или рассеивания
данных.
Основными характеристиками рассеивания являются:
размах (R),
дисперсия (D),
среднеквадратическое (стандартное) отклонение
(σ – сигма),
коэффициент вариации(V).
Слайд 21
Характеристики ассиметрии и эксцесса
Слайд 23
У студентов первого и второго
курса был исследован
уровень
депрессивного расстройства .
Сделать сравнительный анализ,
используя методы
описательной
статистики.
Слайд 24
Оценка центральной тенденции:
Медиана и среднее арифметическое значение на
первом курсе выше, чем на втором, следовательно уровень депрессивного
расстройства на 1 курсе превышает уровень расстройства на втором курсе.
Однако мода на 2-ом курсе значительно выше, чем на первом, т.е. преобладают более высокие значения уровня депрессивного расстройства
Слайд 25
Оценка разброса данных
1 курс 2 курс
дисперсия 37,0 23,9
ст.
отклонение 6,1 4,9
к. вариации 37,5 39,4
Дисперсия и стандартное отклонение
на первом курсе выше, чем на втором, что говорит о более широком разбросе данных и следовательно, можно сделать вывод о том, что вторая выборка более однородна.
Слайд 26
3. Асимметрия и Эксцесс
1 курс 2 курс
ассиметрия 0,9
0,5
эксцесс 0,06 0,64
Первая выборка(1 курс) имеет небольшую положительную левостороннюю
асимметрию (0,9) и незначительный положительный эксцесс (0,06).
Вторая выборка (2 курс) также имеет небольшую положительную ассиметрию (0,5) и положительный эксцесс(0,64).