- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Мультиколлинеарность
Содержание
- 2. Мультиколлинеарность - тесная корреляционная взаимосвязь между отбираемыми для анализа факторами, совместно воздействующими на общий результат.
- 3. Виды мультиколлинеарности. Строгая и нестрогая мультиколлинеарностьСтрогая (полная,
- 4. Полная мультиколлинеарность соответствует случаю, когда
- 5. Корреляционные связи есть всегда. Проблема мультиколлинеарности -
- 6. Мультиколлинеарность проявляется в совместном действии факторов:1. Построить
- 7. В экономических исследованиях мультиколлинеарность чаще проявляется в
- 8. ВНИМАНИЕ! Рассматриваемые в презентации примеры можно найти
- 9. Рекомендуемая литература по теме
- 10. Обнаружение мультиколлинеарностиОдин из подходов заключается в анализе
- 11. ПРИМЕР. Задача состоит в построении модели для
- 12. Обнаружение мультиколлинеарностиВысокие коэффициенты детерминации и F-статистика, но
- 13. Обнаружение мультиколлинеарности. Анализ матрицы коэффициентов парной корреляции
- 14. Обнаружение мультиколлинеарности Тест Фаррара–Глоубера Этот
- 15. Обнаружение мультиколлинеарности Тест Фаррара–Глоубера (1) Проверка
- 16. Обнаружение мультиколлинеарности. Тест Фаррара–Глоубера (1)Проверка наличия мультиколлинеарности
- 17. Обнаружение мультиколлинеарности. Тест Фаррара–Глоубера (2) Проверка наличия
- 18. Обнаружение мультиколлинеарности. Тест Фаррара–Глоубера (2) Проверка наличия
- 19. Обнаружение мультиколлинеарности. Тест Фаррара–Глоубера (3) Проверка наличия мультиколлинеарности каждой пары переменных (t-тест).
- 20. Обнаружение мультиколлинеарности. Тест Фаррара–Глоубера (3) Проверка наличия
- 21. Фактор инфляции вариации как оценка эффекта мультиколлинеарностиДля
- 22. Обнаружение мультиколлинеарности. Метод инфляционных факторовАлгоритм метода заключается
- 23. Минимальное возможное значение = 1.0 Значения VIF j
- 24. Обнаружение мультиколлинеарности. Метод Белсли.Для определения мультиколлинеарности используем
- 25. Скачать презентацию
- 26. Похожие презентации























Слайд 2 Мультиколлинеарность - тесная корреляционная взаимосвязь между отбираемыми для
анализа факторами, совместно воздействующими на общий результат.
Слайд 3
Виды мультиколлинеарности. Строгая и нестрогая мультиколлинеарность
Строгая (полная, функциональная)
мультиколлинеарность - наличие линейной функциональной связи между объясняющими переменными
.2. Нестрогая мультиколлинеарность - наличие сильной линейной корреляционной связи между объясняющими переменными .
3. Чем ближе мультиколлинеарность к строгой
(совершенной), тем серьезнее ее последствия
Слайд 4 Полная мультиколлинеарность соответствует случаю, когда предположение,
что матрица невырождена, т.
е. ее определитель отличен от нуля: ) нарушается, т. е. когда столбцы матрицы линейно зависимы.Это приводит к невозможности решения соответствующей системы нормальных уравнений и получения оценок параметров регрессионной модели.
Слайд 5 Корреляционные связи есть всегда. Проблема мультиколлинеарности - сила
проявления корреляционных связей.
2. Однозначных критериев мультиколлинеарности не существует.
3. Строгая
мультиколлинеарность делает построение регрессии невозможным. (Согласно теоремы Кронекера-Капелли система уравнений имеет бесчисленное множество решений).
Слайд 6
Мультиколлинеарность проявляется в совместном действии факторов:
1. Построить модель
- значит определить вклад каждого фактора.
2. Если два или
более фактора изменяются только совместно, их вклад по отдельности становится невозможно различить.3. Чем более сильно коррелированны переменные, тем труднее различить их вклад.
Слайд 7 В экономических исследованиях мультиколлинеарность чаще проявляется в нестрогой
(стохастической) форме, когда между хотя бы двумя объясняющими переменными
существует тесная корреляционная связь. Определитель матрицы Х'Х не равен нулю, но очень мал. В этом случае затрудняется экономическая интерпретация параметров уравнения регрессии, так как некоторые из его коэффициентов могут иметь неправильные с точки зрения экономической теории знаки и неоправданно большие значения. Оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняются с изменением объема наблюдений (не только по величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования
Слайд 8
ВНИМАНИЕ!
Рассматриваемые в презентации примеры можно найти в
«Экономико-математические методы и модели: компьютерное моделирование: Учебное пособие– 3-е
изд., перераб. и доп. / И.В. Орлова, В.А. Половников. – М.: Вузовский учебник: ИНФРА-М, 2014.» / ЭБС ZNANIUM.COM
Слайд 10
Обнаружение мультиколлинеарности
Один из подходов заключается в анализе матрицы
коэффициентов парной корреляции. Считают явление мультиколлинеарности в исходных данных
установленным, если коэффициент парной корреляции между двумя переменными больше 0,8.Другой подход состоит в исследовании матрицы Х'Х. Если определитель матрицы Х'Х близок к нулю, то это свидетельствует о наличии мультиколлинеарности.
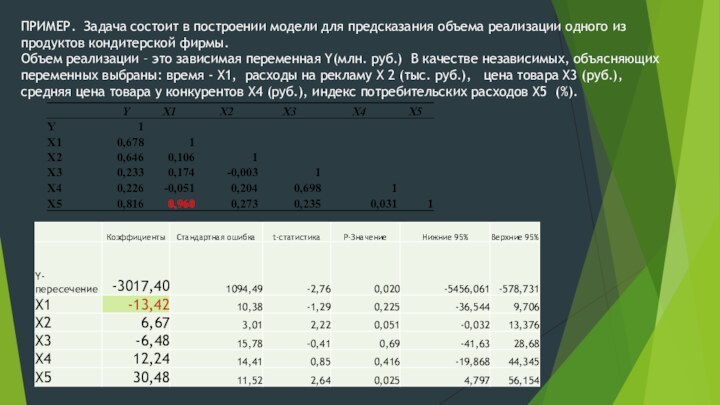
Слайд 11 ПРИМЕР. Задача состоит в построении модели для предсказания
объема реализации одного из продуктов кондитерской фирмы.
Объем реализации –
это зависимая переменная Y(млн. руб.) В качестве независимых, объясняющих переменных выбраны: время - X1, расходы на рекламу X 2 (тыс. руб.), цена товара X3 (руб.), средняя цена товара у конкурентов X4 (руб.), индекс потребительских расходов X5 (%).
Слайд 12
Обнаружение мультиколлинеарности
Высокие коэффициенты детерминации и F-статистика, но некоторые
(или даже все ) коэффициенты незначимы, т.е. имеют низкие
t -статистики.Высокие парные коэффициенты корреляции.
Высокие частные коэффициенты корреляции.
Высокие значения коэффициента VIF («фактор инфляции вариации»).
Знаки коэффициентов регрессии противоположны ожидаемым.
Добавление или удаление наблюдений из выборки сильно изменяют значения оценок.
Слайд 13
Обнаружение мультиколлинеарности. Анализ матрицы коэффициентов парной корреляции
ПРИМЕР. Задача
состоит в построении модели для предсказания объема реализации одного
из продуктов кондитерской фирмы.Объем реализации – это зависимая переменная Y(млн. руб.) В качестве независимых, объясняющих переменных выбраны: время - X1, расходы на рекламу X 2 (тыс. руб.), цена товара X3 (руб.), средняя цена товара у конкурентов X4 (руб.), индекс потребительских расходов X5 (%).
Слайд 14
Обнаружение мультиколлинеарности
Тест Фаррара–Глоубера
Этот алгоритм содержит
три вида статистических критериев проверки наличия мультиколлинеарности:
1) всего массива переменных
(критерий «хи-квадрат»);2) каждой переменной с другими переменными (F-критерий);
3) каждой пары переменных (t-тест).
Слайд 15 Обнаружение мультиколлинеарности Тест Фаррара–Глоубера (1) Проверка наличия мультиколлинеарности всего
массива переменных (критерий «хи-квадрат») • Построить корреляционную матрицу R и найти
её определитель • Вычислить наблюдаемое значение статистики Фаррара – Глобера по следующей формуле: Эта статистика имеет распределение (хи-квадрат).
• Фактическое значение этого критерия сравнивается с табличным значением с 0,5k(k-1) степенями свободы и уровне значимости α. Если больше табличного, то в массиве объясняющих переменных существует мультиколлинеарность.
Слайд 16
Обнаружение мультиколлинеарности. Тест Фаррара–Глоубера (1)
Проверка наличия мультиколлинеарности всего
массива переменных
Вычислим определитель матрицы R = 0,373. Вычислим FGнабл:
FGнабл
> FGкрит=12,59 Hо отклоняется, факторы признаются коллинеарными Слайд 17 Обнаружение мультиколлинеарности. Тест Фаррара–Глоубера (2) Проверка наличия мультиколлинеарности каждой
переменной с другими переменными (F-критерий)
1. Вычислить обратную матрицу
2. Вычислить F-критерии
где
– диагональные элементы матрицы C.
3 Фактические значения F критериев сравнить с табличным значением при 1= k и 2 = (n - k – 1) степенях свободы и уровне значимости α, где k – количество факторов. Если , то соответствующая j-тая независимая переменная мультиколлинеарна с другими.
Слайд 18 Обнаружение мультиколлинеарности. Тест Фаррара–Глоубера (2) Проверка наличия мультиколлинеарности каждой
переменной с другими переменными (F-критерий)
2. Вычислим F-критерии
3.
Табличное значение F-критерия =
3,36
4. 3 и 4-ая независимые переменные мультиколлинеарнаы с другими.
Слайд 19 Обнаружение мультиколлинеарности. Тест Фаррара–Глоубера (3) Проверка наличия мультиколлинеарности каждой
пары переменных (t-тест).
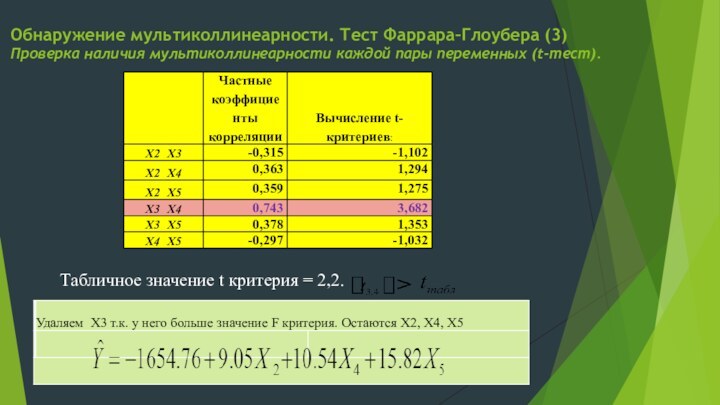
Слайд 20 Обнаружение мультиколлинеарности. Тест Фаррара–Глоубера (3) Проверка наличия мультиколлинеарности каждой
пары переменных (t-тест).
Табличное значение t критерия = 2,2.
Слайд 21
Фактор инфляции вариации как оценка эффекта мультиколлинеарности
Для измерения
эффекта мультиколлинеарности используется показатель VIF – «фактор инфляции вариации»
Слайд 22
Обнаружение мультиколлинеарности. Метод инфляционных факторов
Алгоритм метода заключается в
следующем:
1.Строятся уравнения регрессии, которые связывают каждый из регрессоров
со всеми оставшимися.2. Вычисляются коэффициенты детерминации R2 для каждого уравнения регрессии.
3. Проверяется статистическая гипотеза H0: R2=0 с помощью F теста. Вывод: если гипотеза H0: R2=0 не отклоняется, значит данный регрессор не приводит к мультиколлинеарности.
4. Значения VIF j > 10.0 могут указывать на наличие мультиколлинеарности.
Слайд 23
Минимальное возможное значение = 1.0
Значения VIF j >
10.0 могут указывать на наличие мультиколлинеарности
X1 21,112 X2 1,889
X3 2,474
X4 2,331
X5 23,389
Обнаружение мультиколлинеарности. Метод инфляционных факторов
Слайд 24
Обнаружение мультиколлинеарности. Метод Белсли.
Для определения мультиколлинеарности используем метод
Белсли. Belsley, Kuh и Welsch предложили метод анализа мультиколлинеарности
основанный на индексах обусловленности (the scaled condition indexes) и дисперсионных долях (the variance-decomposition proportions). Обусловленность оценивает близость матрицы коэффициентов к вырожденной. Число обусловленности η является количественной оценкой обусловленности . Отметим, что всегда η> 1. Если η > 103, то говорят, что матрица плохо обусловлена. Если 1 < η < 100 , то матрица считается хорошо обусловленной.Оценки собственных значений
96,65=32,36/0,33





























