Слайд 2
Раскраска графов
Определение. Пусть G=(V, E) – неориентированный граф
и k – натуральное число.
Функция f: V{1,…,k} называется
раскраской графа.
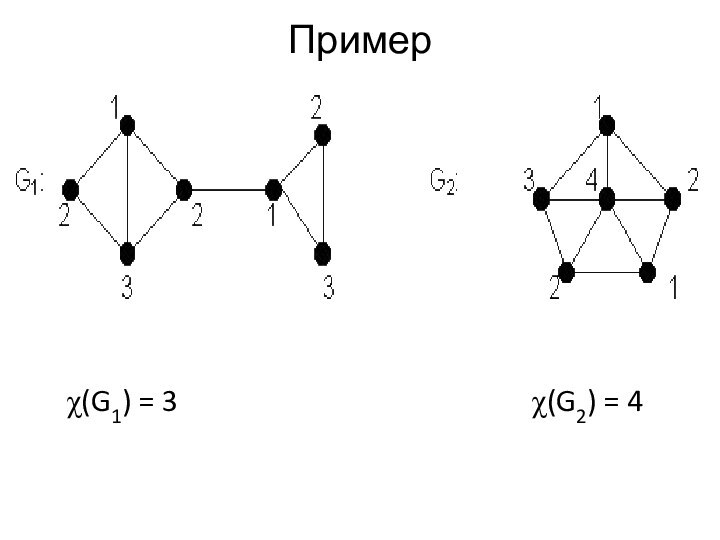
Раскраска называется правильной, если для любых смежных вершин x,yV справедливо неравенство f(x) ≠ f(y). Число k – количество красок раскраски f.
Определение. Наименьшее число красок, необходимое для правильной раскраски графа G называется хроматическим числом графа G.
Правильную раскраску таким числом красок будем называть оптимальной.
Хроматическое число обозначается через χ(G).
Слайд 4
Задача составления расписаний
Предположим, что в учебном центре надо
провести несколько занятий за кратчайшее время.
Длительность всех занятий
одинакова, скажем, один час. Некоторые занятия не могут проводиться одновременно, например, это занятия в одной и той же учебной группе (по разным предметам), или занятия проводит один и тот же преподаватель.
Для решения задачи построим граф G, вершинам которого взаимнооднозначно соответствуют занятия. Две вершины соединены ребром, если соответствующие занятия нельзя проводить одновременно.
Ясно, что правильная раскраска графа G определяет расписание, удовлетворяющее требованиям несовместимости по времени: занятия, соответствующие вершинам, окрашенным одинаково, можно проводить одновременно.
Справедливо и обратное, любое такое расписание определяет правильную раскраску графа G. Следовательно, кратчайшее время необходимое для проведения всех занятий равно χ(G), а из оптимальной раскраски графа G получается необходимое расписание.
Слайд 5
Задача распределения ресурсов
Необходимо выполнить некоторое множество V={v1,v2,…,vn}
работ.
Имеется множество S={s1,s2,…,sr} ресурсов, необходимых для выполнения этих
работ.
Каждая работа использует часть указанных ресурсов.
Одновременно могут выполняться работы, использующие разные ресурсы.
Все работы выполняются за одно и то же время t.
Необходимо распределить ресурсы так, чтобы общее время выполнения всех работ было минимальным.
Рассмотрим граф G с множеством вершин V. Две различные вершины v и v’ графа G смежны тогда и только тогда, когда для выполнения работ v и v’ требуется хотя бы один общий ресурс.
Наименьшее время выполнения всех работ равно χ(G)·t.
Оптимальная раскраска графа G определяет распределение ресурсов.
Слайд 6
Задача экономии памяти
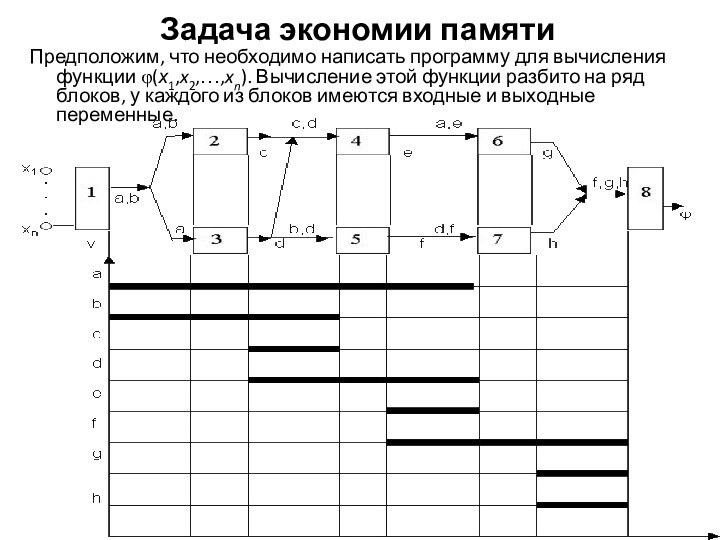
Предположим, что необходимо написать программу для
вычисления функции φ(х1,x2,…,xn). Вычисление этой функции разбито на ряд
блоков, у каждого из блоков имеются входные и выходные переменные.
Слайд 7
Задача экономии памяти (продолжение)
Предположим, что значения переменной занимают
одну ячейку памяти.
Задача состоит в том, чтобы определить
наименьшее число ячеек памяти, необходимое для хранения указанных в блок – схеме переменных.
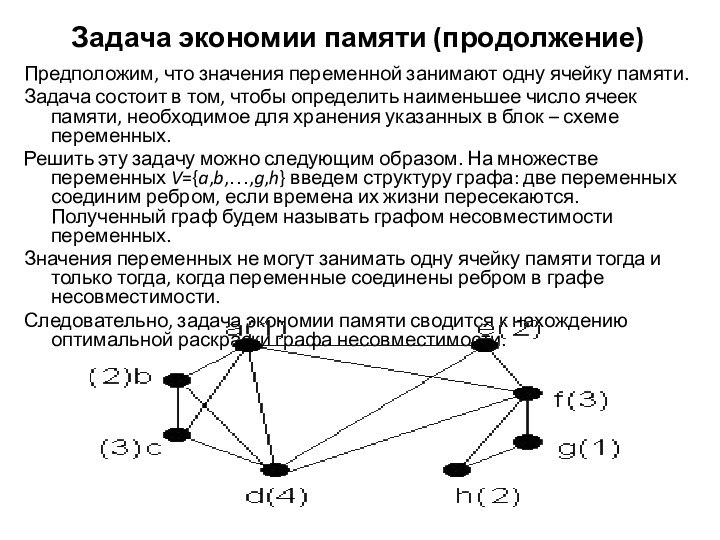
Решить эту задачу можно следующим образом. На множестве переменных V={a,b,…,g,h} введем структуру графа: две переменных соединим ребром, если времена их жизни пересекаются. Полученный граф будем называть графом несовместимости переменных.
Значения переменных не могут занимать одну ячейку памяти тогда и только тогда, когда переменные соединены ребром в графе несовместимости.
Следовательно, задача экономии памяти сводится к нахождению оптимальной раскраски графа несовместимости.
Слайд 8
Алгоритм последовательной раскраски
Упорядочиваем вершины графа G: V={v1,v2,…,vn}.
Вершину v1
красим первой краской.
Предположим, что вершины v1,…,vi уже раскрашены
и на это использовано k красок.
Если на раскрашенные вершины, смежные с vi+1, использованы все краски, то vi+1 раскрашиваем k+1 краской.
Если среди k красок найдется краска, которая не использована для вершин, смежных с vi+1, то вершину vi+1 красим этой краской.
1
2
4
3
7
6
5
8
9
10
11
12
1
2
3
4
Слайд 9
Проблема четырех красок
Проблема возникла в математике в середине
19 века.
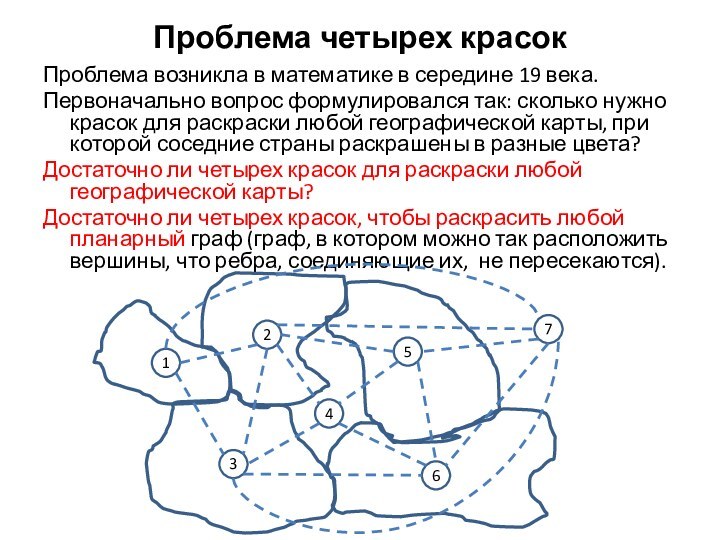
Первоначально вопрос формулировался так: сколько нужно красок
для раскраски любой географической карты, при которой соседние страны раскрашены в разные цвета?
Достаточно ли четырех красок для раскраски любой географической карты?
Достаточно ли четырех красок, чтобы раскрасить любой планарный граф (граф, в котором можно так расположить вершины, что ребра, соединяющие их, не пересекаются).
1
2
3
4
5
6
7
Слайд 10
Проблема четырех красок
Эта проблема вызвала большой интерес в
математике.
Есть свидетельства, что ей занимались известные математики Мебиус
и де Морган.
В 1880 году А. Компе опубликовал положительное решение проблемы четырех красок.
Однако в 1890 году Р. Хивуд обнаружил ошибку в этом доказательстве. Он доказал, что любой планарный граф можно раскрасить пятью красками.
После этого появлялось довольно много «доказательств» гипотезы четырех красок и «контрпримеров» к ней, в которых обнаруживались ошибки.
Слайд 11
Проблема четырех красок (продолжение)
В 1969 году Х. Хели свел
проблему четырех красок к исследованию множества С так называемых
неустранимых конфигураций. Множество С является конечным. Но довольно большим (порядка нескольких тысяч).
Несколькими годами позже, в 1976 году математикам К. Аппелю и В. Хейкену удалось показать, что все конфигурации из множества С можно правильно раскрасить в четыре цвета. В возникающем при этом переборе существенно использовался компьютер.
Такое решение проблемы четырех красок долгое время не признавалось многими математиками, поскольку его сложно повторить. Однако сейчас практически общепризнано, что К. Аппелем и В. Хейкеном доказана гипотеза четырех красок.
Слайд 12
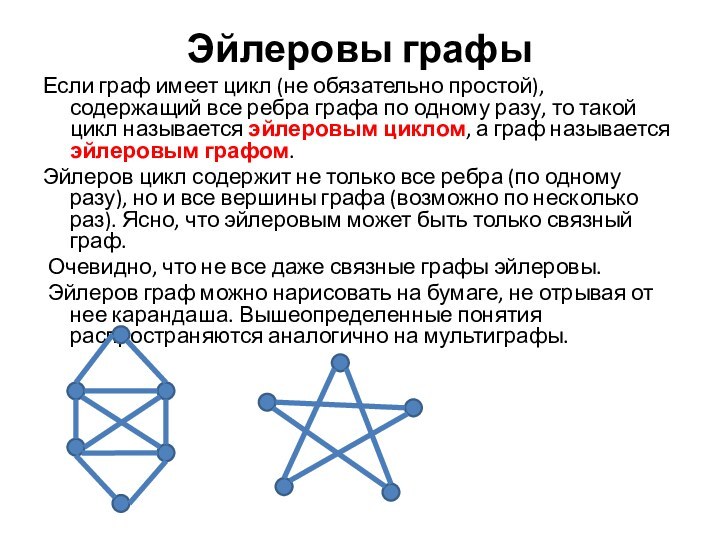
Эйлеровы графы
Если граф имеет цикл (не обязательно простой),
содержащий все ребра графа по одному разу, то такой
цикл называется эйлеровым циклом, а граф называется эйлеровым графом.
Эйлеров цикл содержит не только все ребра (по одному разу), но и все вершины графа (возможно по несколько раз). Ясно, что эйлеровым может быть только связный граф.
Очевидно, что не все даже связные графы эйлеровы.
Эйлеров граф можно нарисовать на бумаге, не отрывая от нее карандаша. Вышеопределенные понятия распространяются аналогично на мультиграфы.
Слайд 13
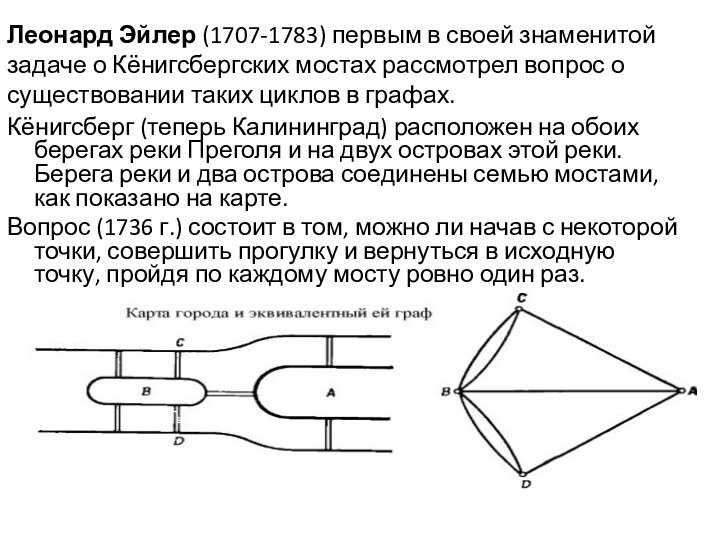
Леонард Эйлер (1707-1783) первым в своей знаменитой задаче
о Кёнигсбергских мостах рассмотрел вопрос о существовании таких циклов
в графах.
Кёнигсберг (теперь Калининград) расположен на обоих берегах реки Преголя и на двух островах этой реки. Берега реки и два острова соединены семью мостами, как показано на карте.
Вопрос (1736 г.) состоит в том, можно ли начав с некоторой точки, совершить прогулку и вернуться в исходную точку, пройдя по каждому мосту ровно один раз.
Слайд 14
Теорема
Если неориентированный граф G связен и в нем
более одной вершины, то следующие утверждения эквивалентны:
G — эйлеров
граф.
Каждая вершина G имеет четную степень.
Множество ребер G можно разбить на простые циклы.
Слайд 15
Алгоритмы поиска эйлерова цикла
Алгоритм Флёри ( сложность O(n*(n+m))
Требуется
занумеровать ребра графа числами 1, 2, …, |E|, так,
чтобы номер, присвоенный ребру, указывал, каким по счету это ребро проходится в эйлеровом цикле.
Начиная с произвольной вершины u, присваиваем произвольному ребру (u,v) номер 1. Затем вычеркиваем ребро (u,v) из графа и переходим в вершину v.
Пусть w – вершина, в которую мы пришли в результате выполнения предыдущего шага, и k – номер, присвоенный некоторому ребру на этом шаге. Выбираем любое ребро, инцидентное вершине w, причем мост выбираем только в том случае, если нет других возможностей; присваиваем выбранному ребру номер k + 1, проходим по нему в следующую вершину и вычеркиваем его .
Алгоритм заканчивается, когда все ребра вычеркнуты
Мост – ребро, удаление которого из графа приводит к тому, что граф распадается на несколько компонент связности.
Слайд 16
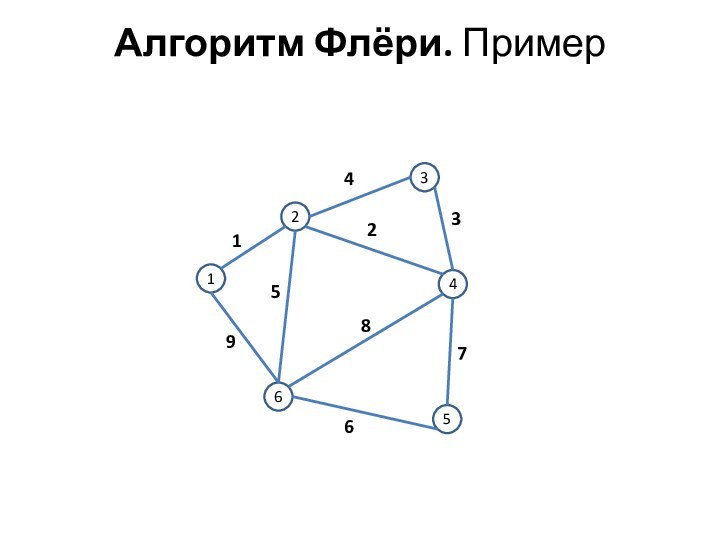
Алгоритм Флёри. Пример
1
2
4
3
6
5
1
2
3
4
5
6
7
8
9
Слайд 17
Алгоритм поиска эйлерового цикла (О(m))
Начиная с произвольной вершины,
строим путь, удаляя ребра и запоминая вершины в стеке,
до тех пор пока множество смежности очередной вершины не окажется пустым, что означает, что путь удлинить нельзя.
Заметим, что при этом мы с необходимостью придем в ту вершину, с которой начали. В противном случае это означало бы, что вершина v имеет нечетную степень, что невозможно по условию.
Таким образом, из графа были удалены ребра цикла, а вершины цикла были сохранены в стеке S. Заметим, что при этом степени всех вершин остались четными. Далее вершина v выводится в качестве первой вершины эйлерового цикла, а процесс продолжается, начиная с вершины, стоящей на вершине стека.
Слайд 18
Алгоритм
Вход: эйлеров граф G(V, E), заданный списками смежности (Γ[v] —
список вершин смежных с вершиной v).
Выход: последовательность вершин
эйлерового цикла.
S := Ø { стек для хранения вершин }
выбрать v ∈ V { произвольная вершина }
v → S { положить v в стек S }
пока S ≠ Ø выполнять
v ← S; v → S { v — верхний элемент стека }
если Γ[v] = Ø
то v ← S; вывод v
иначе
выбрать u ∈ Γ[v]
{ взять первую вершину из списка смежности }
u → S
Γ[v] := Γ[v] \ {u};
Γ[u] := Γ[u] \ {v} { удалить ребро (v, u) }
конец если
конец пока
Слайд 19
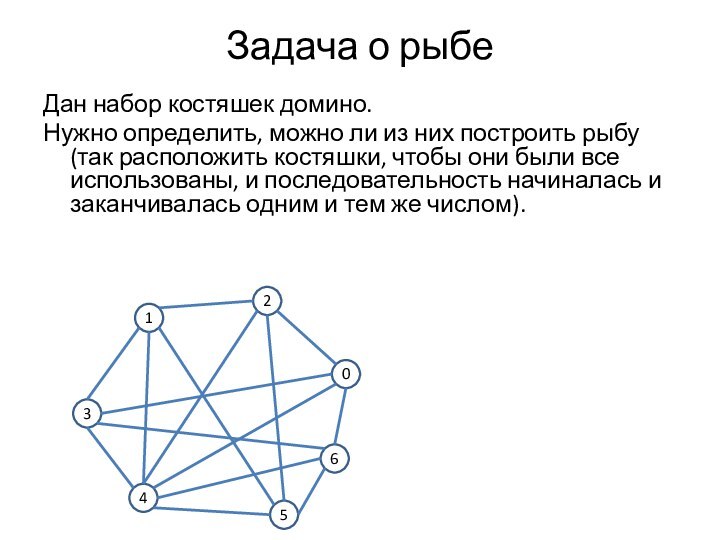
Задача о рыбе
Дан набор костяшек домино.
Нужно определить,
можно ли из них построить рыбу (так расположить костяшки,
чтобы они были все использованы, и последовательность начиналась и заканчивалась одним и тем же числом).
1
2
4
3
0
6
5
Слайд 20
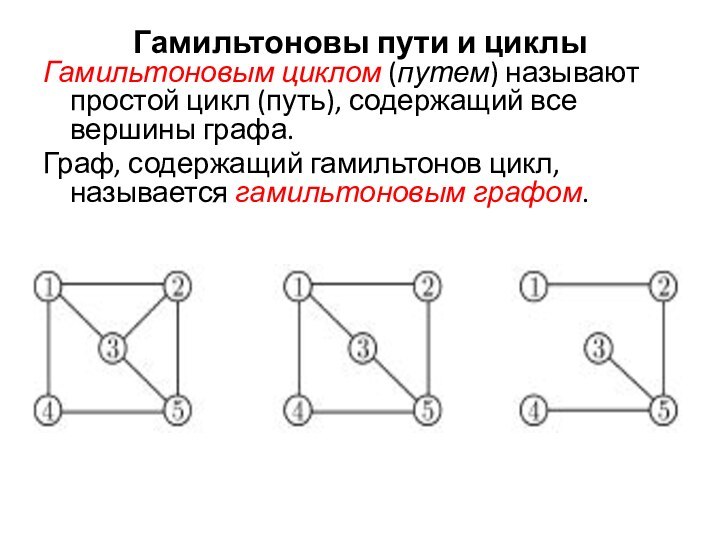
Гамильтоновы пути и циклы
Гамильтоновым циклом (путем) называют простой
цикл (путь), содержащий все вершины графа.
Граф, содержащий гамильтонов цикл,
называется гамильтоновым графом.
Слайд 21
Алгоритм. Поиск гамильтоновых циклов
выбрать произвольную вершину a
a
PATH
N(a) V(a) //вершины, смежные с а
пока PATH ≠
выполнять
x top(PATH)
если N(x) ≠
то взять y N(x)
N(x) N(x) - y
если вершина y не находится в PATH
то y PATH
N(y) V(y)
если PATH содержит все вершины
то если y смежна с a
то выдать цикл
иначе удалить вершину x из PATH
Слайд 22
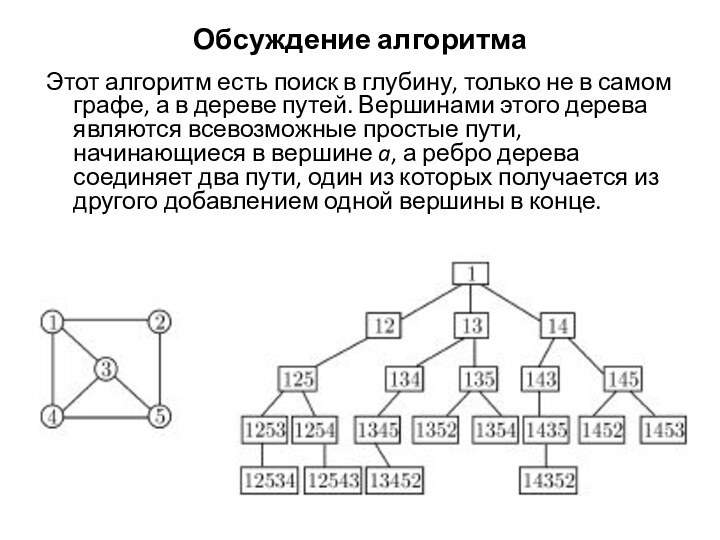
Обсуждение алгоритма
Этот алгоритм есть поиск в глубину, только
не в самом графе, а в дереве путей. Вершинами
этого дерева являются всевозможные простые пути, начинающиеся в вершине a, а ребро дерева соединяет два пути, один из которых получается из другого добавлением одной вершины в конце.
Слайд 23
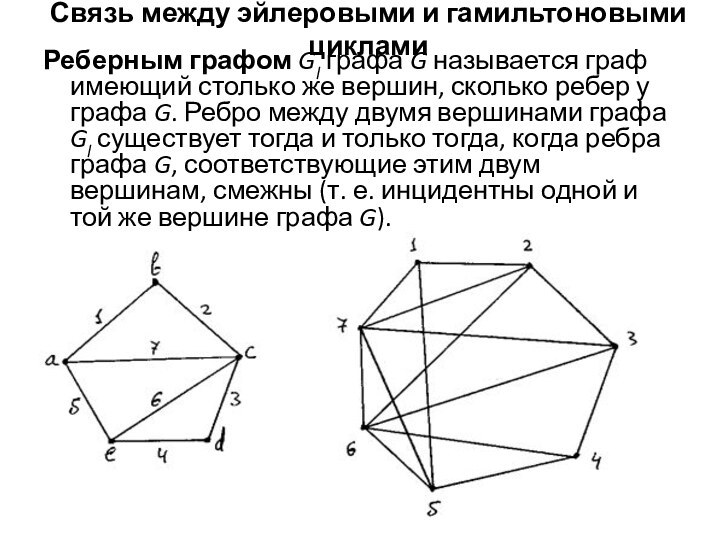
Связь между эйлеровыми и гамильтоновыми циклами
Реберным графом Gl
графа G называется граф имеющий столько же вершин, сколько
ребер у графа G. Ребро между двумя вершинами графа Gl существует тогда и только тогда, когда ребра графа G, соответствующие этим двум вершинам, смежны (т. е. инцидентны одной и той же вершине графа G).










![Лекция 12 АлгоритмВход: эйлеров граф G(V, E), заданный списками смежности (Γ[v] — список вершин смежных с](/img/tmb/14/1347302/0cb3e4bad753d20472dacff242b786fa-720x.jpg)