Слайд 2
Тематическое построение учебника и тетради.
Слайд 3
Состоит из двух блоков:
Узнаём новое(содержит новый материал: теоретические
сведения, проблемные вопросы и задания. Материал предназначен для первичного
ознакомления и не претендует на немедленное усвоение)
Вспоминаем пройденное (служит для повторения, закрепления и расширения полученных знаний, совершенствования умений и выработки определённых навыков. При этом содержание может иметь некоторые элементы новизны: новый поворот сюжета текстовой задачи, другой способ решения, новый вид упражнений)
Слайд 4
Рубрика «Путешествие в прошлое» носит ознакомительный характер. Раскрывает
учащимся некоторые доступные сведения из истории математики. Иногда предлагаются
старинные задачи, головоломки. Занимательные упражнения.
Слайд 5
Устный счёт
В.Н. Рудницкая, Т.В.Юдачёва «Устные вычисления»
Методическое пособие
Часть
методики преподавания. Материал разбит по классам и темам.
Продолжительность устных
вычислений : 5-7 минут.
Необходимо выбирать приёмы вычислений, удобные для каждого
конкретного урока, опираясь на подготовленность класса
Устные упражнения могут предлагаться на разных этапах урока:
В начале урока, как подготовка
В середине урока, как первичное закрепление новой темы
В тот момент, когда учитель замечает рассеянное внимание детей.
В этом случае такая работа внесет разнообразие , оживит, «встряхнёт»
класс.
Слайд 6
Виды устного счёта:
математический диктант(включая терминологию)
Игра
Математический кроссворд
Слайд 7
Основные цели обучения в курсе «Математика»
Существенно повысить уровень
интеллектуального и математического
развития детей.
Развитие логико-математических понятий и отношений.
Алгебраическая пропедевтика,
основы математического анализа
Особенность курса заключается в том, что даже при повторении и
закреплении уже полученных знаний детям предлагаются задачи и
упражнения, которые расширяют уже полученные знания.
Слайд 8
Важными структурными элементами урока являются:
Совместная работа учителя и
учащихся по постановке учебной задачи и обсуждение способов её
решения.
Самостоятельная деятельность школьников по оформлению решения учебной задачи.
Проверка и взаимопроверка.
Работа учащихся в парах и группах.
Организация дидактических игр.
Работа с текстом учебника: обучение чтению и пониманию математического текста.
Слайд 9
Содержательные линии курса
Элементы арифметики
Логико-математические понятия и отношения
Величины и
их измерения
Элементы геометрии
Алгебраическая пропедевтика
Включены так же темы, которые носят
ознакомительный( фоновый) характер. Их около 20.
1 класс -2 темы (Симметрия. Ось симметрии.)
2 класс – 2-3 темы
3 класс – 4-6 тем
4 класс – 13 тем.
Эти темы располагаются на зелёном фоне.
Слайд 10
Моделирование, как использование внутренних особенностей детей для изучения
математики.
Слайд 11
1-я модель. Фишки.( 1 класс)
С опорой на фишки
обучение выполнению всех 4 математических действий.
Решение задач.
Умножение и деление.
Слайд 12
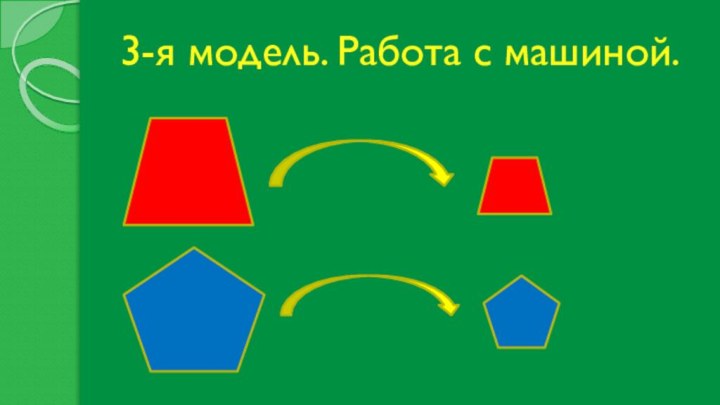
2-я модель. Цветные фигуры.
Обобщение знаний о математических фигурах.
Классификация
.( Для классификации должна быть чёткая формулировка). Опираясь на
правило разбивать фигуры на классы.
Самим придумывать значимые основания для классификации.
Слайд 14
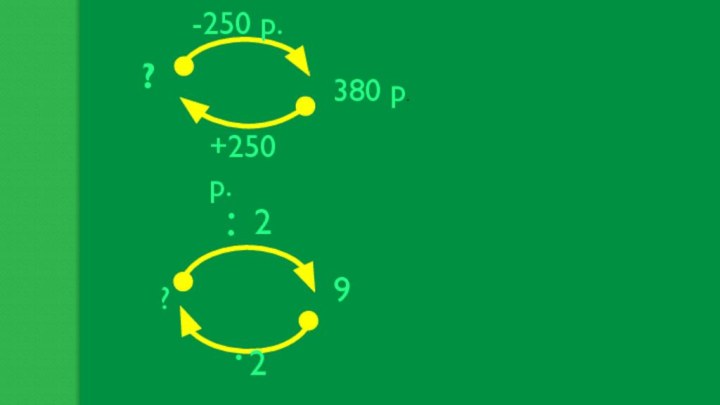
Машина – как вспомогательное средство для решения задачи.
краткая запись ( устаревший способ)
Чертёж
Схема
Отрезки(несложные задачи с величинами)
Слайд 16
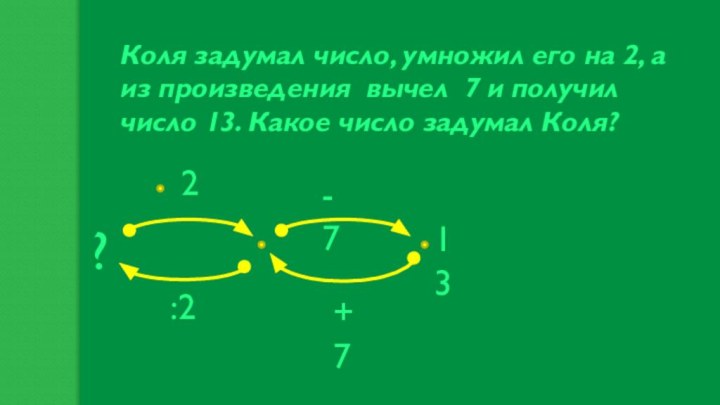
Коля задумал число, умножил его на 2, а
из произведения вычел 7 и получил число 13. Какое
число задумал Коля?
?
13
2
- 7
+7
:2
Слайд 17
Использование графов
Для отработки понятий «больше на…», «больше в…»,
«меньше на…», «меньше в…».
В гардеробе 43 пальто, плащей на
12 больше, а курток на 4 меньше. Сколько курток в гардеробе?
Пл.
К.
На 12 б.
На 4 м.
Задача в косвенной форме
36 значков
В 3 раза б.
В 3 раза м.
Слайд 19
Известно, что карандаш дороже тетради, блокнот дешевле тетради,
блокнот дороже ручки, линейка дешевле ручки. Какой предмет дороже
всех остальных?
К
Т
Б
Р
Л
Слайд 20
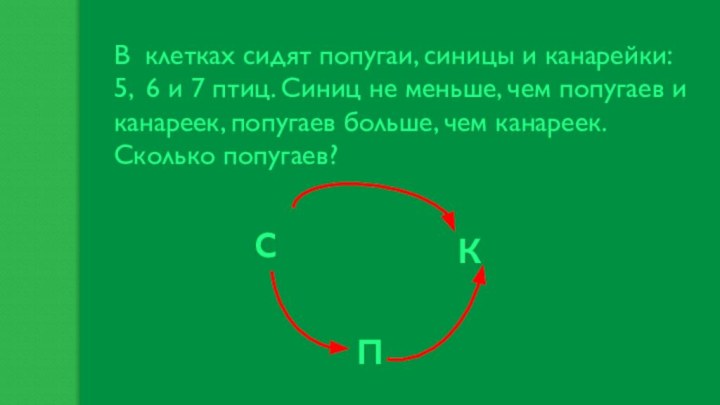
В клетках сидят попугаи, синицы и канарейки: 5,
6 и 7 птиц. Синиц не меньше, чем попугаев
и канареек, попугаев больше, чем канареек. Сколько попугаев?
с
п
к
Слайд 21
Письменный алгоритм деления.
Случаи, когда в частном только одна
цифра
Используем метод подбора.
2 3 4 5 6 7 8 9
144:24 =
24 Х 5 = 120 24 х 7 = 168 24 х 6 = 144
Начинаем подбирать от середины числового рада и ведём подбор через единицу.
Слайд 22
Деление с остатком.
8 : 12 = 0 (остаток
Слайд 23
Письменный алгоритм деления
Случаи деления, когда в частном одна
цифра.
Деление с остатком.
Деление трёхзначного на однозначное.
416 4
4
1
0
16
16
0
104
Слайд 24
Способ работы с частями при нахождении значения числовых
выражений.
3 40 – 20 (65-55) + 81 :
( 36: 4)
120 100 9
Находим действия сложения и вычитания, не заключённые в скобки и обводим их.
Выполняем действия в частях.
Слайд 25
Текстовые арифметические задачи
Отработка арифметических действий.
Развитие мышления.
Не всё нужно
записывать, но всё нужно разбирать.
Слайд 26
Преобразование и составление задач
Решать задачу с недостатком данных
с предложенными детьми вариантами.
Учить детей видеть неточности и доводить
решение до конца.
Дима собрал 120 грибов, а Коля в 3 раза больше. Вместе мальчики нашли 160 опят. Сколько опят собрал Коля?
Задача с лишними неправильными данными.
Слайд 27
Сумма трёх чисел, следующих при счёте одно за
другим, равна 40. Одно из чисел- 26. Какие два
других?
Исследование текста задачи.
Слайд 28
Неарифметические способы решения задач
Метод подбора
В вазе лежат груши,
яблоки, апельсины. Яблок на 2 больше, чем груш. Сколько
фруктов каждого вида, если их всего 5?
Г. - ? Г. - 1 Г. - 2 Не
Яб. - ?на 2 б. Яб.- 3 Яб. – 4 имеет
Ап. - ? Ап. - 1 Ап.- решения
Слайд 29
Метод выявления закономерности
Для установки забора строители установили в
ряд 15 столбов. Сколько понадобится щитов между столбами.
Слайд 30
Рассуждение от противного
В парке растут 18 деревьев семи
разных видов. Верно ли, что в парке не менее
3-х деревьев каждого вида?
Слайд 31
Алгебраический способ
Решение задачи путём составления уравнения, либо выражения
с окошками.
Слайд 32
Линия логического развития
Логические
понятия:
высказывание
Логические
умения:
Сравнение
Анализ
Синтез
Обобщение
Выявление
закономерностей
Приведение подтверждающих и
опровергающих примеров
Логические
Операции
Классификация
Подведение под определение
Слайд 33
Задачи на логику
Выявление закономерности.
Задачи на логические возможности.
Подведение под
определение.
Построение простейших доказательств.
Слайд 34
Работа по алгоритму
Является ли прямоугольник со сторонами 2
см и 4 см квадратом?
Вспоминаем и формулируем определение квадрата.
Выделяем
и формулируем признаки данной фигуры.
Проверяем выполнение выделенных признаков.
Первое требование выполняется.
Второе требование не выполняется.
Вывод: если выполняются ВСЕ требования – то это квадрат. Если хотя бы один признак не подходит под определение – то не квадрат.
Слайд 35
Геометрические фигуры
1 класс
2 класс 3 класс 4 класс
Точка луч ломаная знакомство
Отрезок окружность прямая с транспор-
Круг угол(прямой, тиром, углы
Треугольник непрямой) и их постро-
Прямоугольник многоугольники ение
квадрат прямоугольный
параллелепипед
Слайд 36
Знакомство с многогранниками
Работа с чертежами.
Называние граней, поверхностей, рёбер,
сторон, вершин.
Моделирование из спичек и пластилина.
Уделить особое внимание правильным
названиям фигур.
Фигура должна иметь алгоритм построения.
Слайд 37
Расположение фигур на плоскости
Использование фишек.
Почему случай пересечения под
прямым углом – особый.
Слайд 38
Осевая симметрия
Использование прямоугольного зеркальца обязательно.
Обратить внимание на расположение
точек на той же прямой , расположенной под прямым
углом к оси и на том же расстоянии от оси симметрии.
Слайд 39
Выражения
Числовые
С окошечком:
( +3)
: 2
Буквенные
15 – (х :2)
Слайд 40
Равенства и неравенства
Числовые равенства и их свойства
Числовые неравенства
Равенства
с окошечками
+ 6 = 9
6 : = 3
? 9
9 – 6 = 3 6 : 2 = 3
3 + 6 = 9 6 : 3 = 2
Ответ: 3 Ответ: 2
+6
-6
6 = 3
:?
Правило разностного и кратного сравнения. Вышло число больше или меньше?
А в математике в таких равенствах принято писать букву. Равенство с буквой х + 94 = 126.