Слайд 2
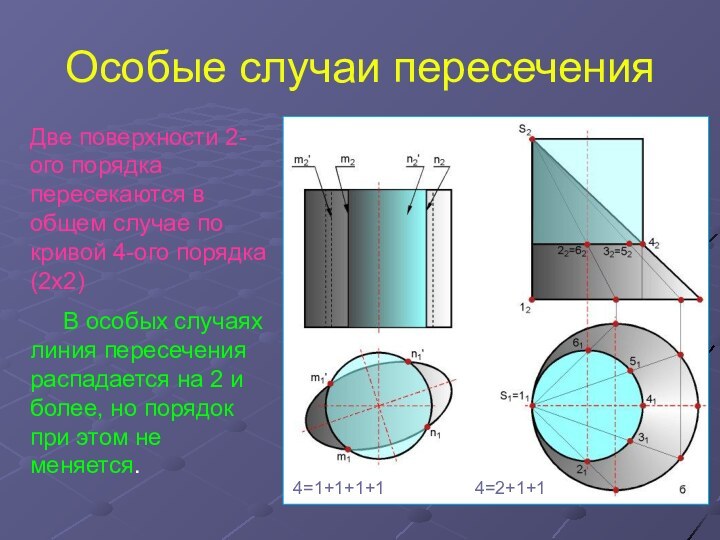
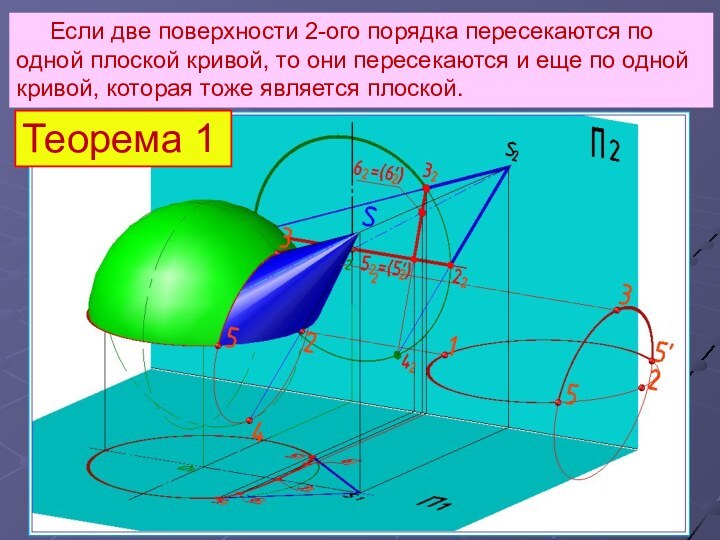
Если две поверхности 2-ого порядка
пересекаются по одной плоской кривой, то они пересекаются и
еще по одной кривой, которая тоже является плоской.
Теорема 1
Слайд 3
Теорема 1
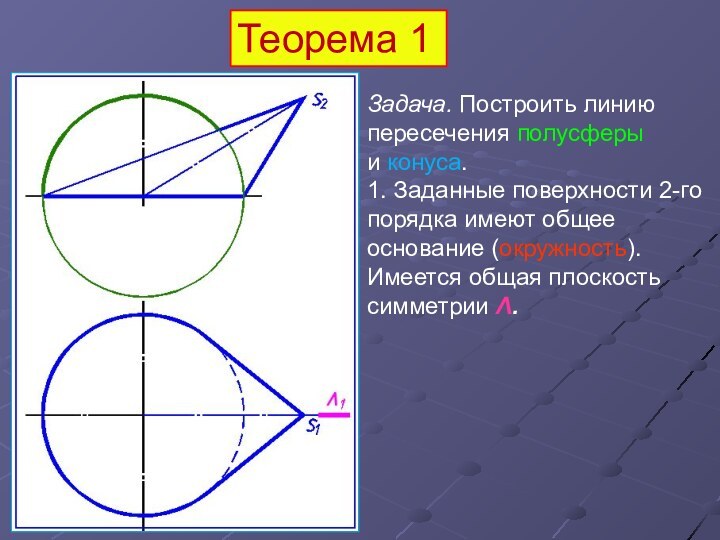
Задача. Построить линию пересечения полусферы
и конуса.
1.
Заданные поверхности 2-го порядка имеют общее основание (окружность).
Имеется общая
плоскость симметрии Λ.
Слайд 4
Теорема 1
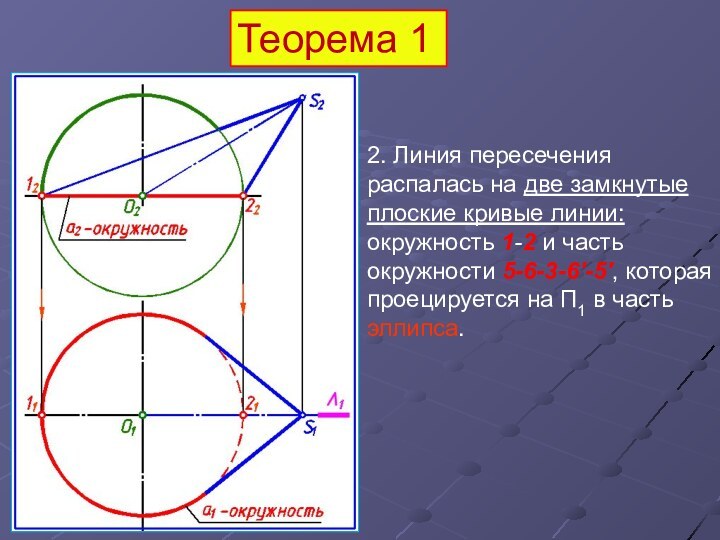
2. Линия пересечения распалась на две замкнутые
плоские кривые линии: окружность 1-2 и часть окружности 5-6-3-6'-5',
которая проецируется на П1 в часть эллипса.
Слайд 5
Теорема 1
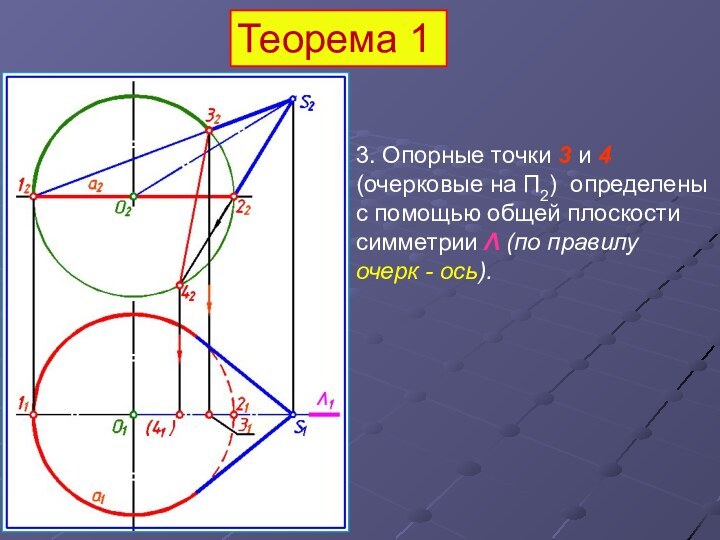
3. Опорные точки 3 и 4 (очерковые
на П2) определены с помощью общей плоскости симметрии Λ
(по правилу
очерк - ось).
Слайд 6
Теорема 1
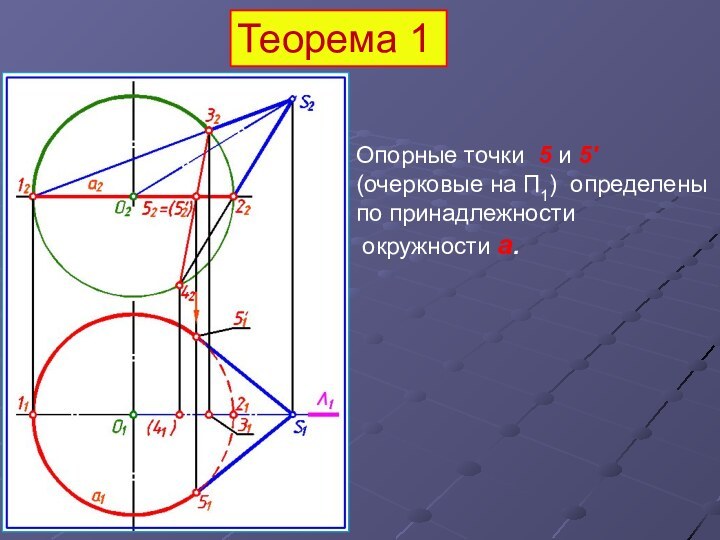
Опорные точки 5 и 5' (очерковые на
П1) определены по принадлежности
окружности а.
Слайд 7
Теорема 1
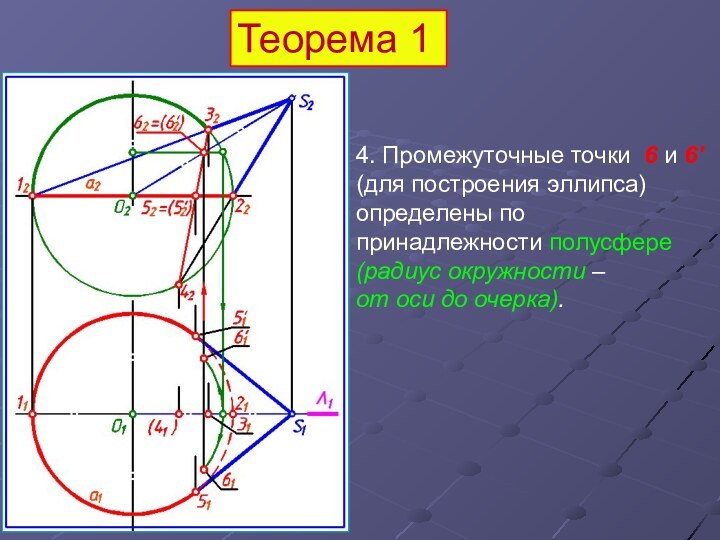
4. Промежуточные точки 6 и 6' (для
построения эллипса) определены по принадлежности полусфере
(радиус окружности –
от
оси до очерка).
Слайд 8
Теорема 1
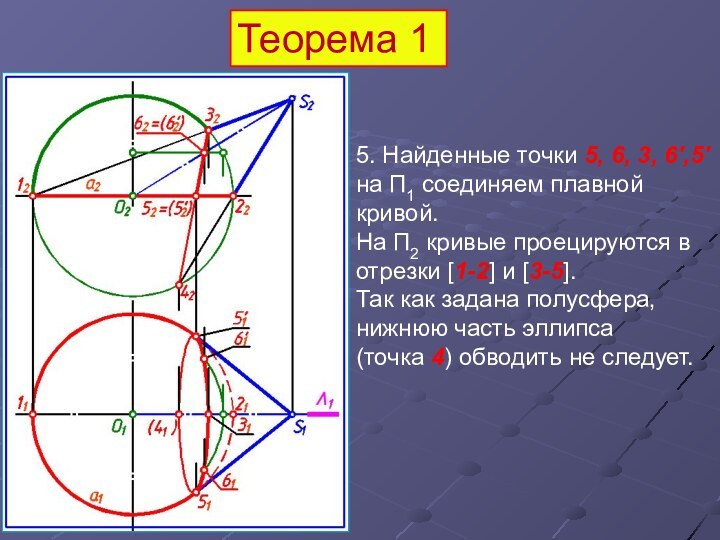
5. Найденные точки 5, 6, 3, 6',5'
на П1 соединяем плавной кривой.
На П2 кривые проецируются в
отрезки [1-2] и [3-5].
Так как задана полусфера, нижнюю часть эллипса
(точка 4) обводить не следует.
Слайд 9
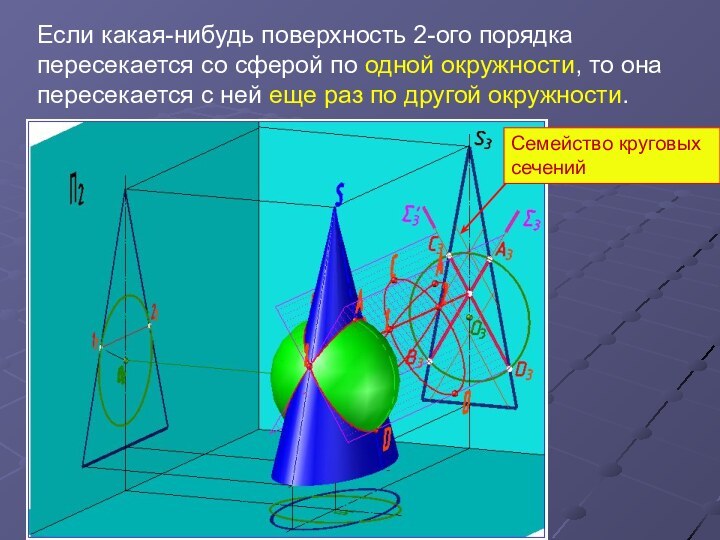
Если какая-нибудь поверхность 2-ого порядка пересекается со сферой
по одной окружности, то она пересекается с ней еще
раз по другой окружности.
Семейство круговых сечений
Слайд 10
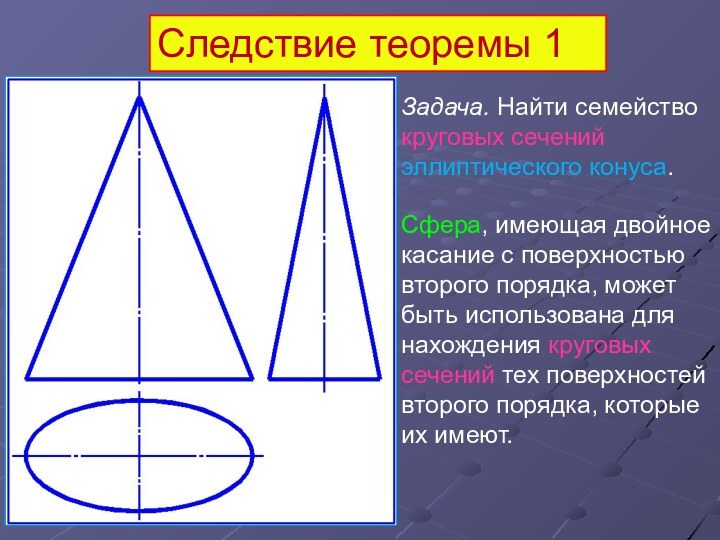
Следствие теоремы 1
Задача. Найти семейство круговых сечений эллиптического
конуса.
Сфера, имеющая двойное касание с поверхностью второго порядка, может
быть использована для нахождения круговых сечений тех поверхностей второго порядка, которые их имеют.
Слайд 11
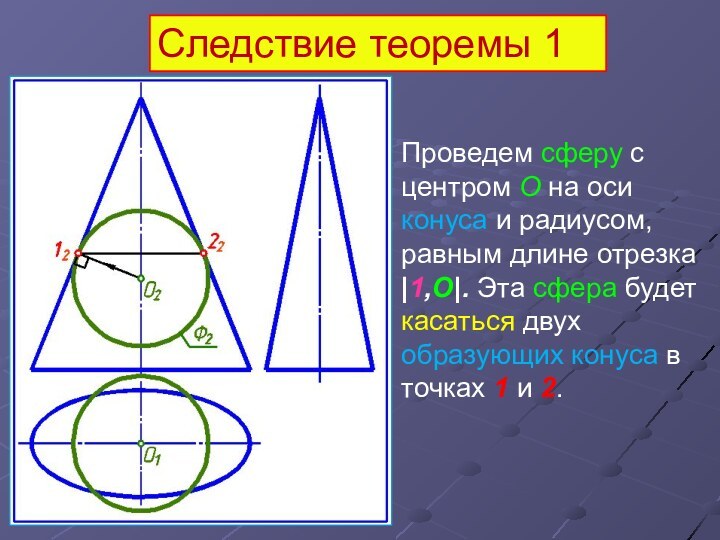
Следствие теоремы 1
Проведем сферу с центром О на
оси конуса и радиусом, равным длине отрезка |1,О|. Эта
сфера будет касаться двух образующих конуса в точках 1 и 2.
Слайд 12
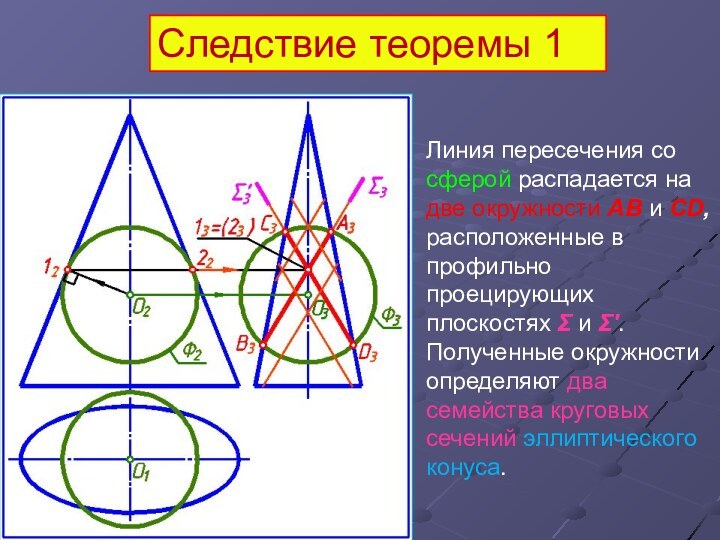
Следствие теоремы 1
Линия пересечения со сферой распадается на
две окружности АВ и СD, расположенные в профильно проецирующих
плоскостях Σ и Σ'.
Полученные окружности определяют два семейства круговых сечений эллиптического конуса.
Слайд 13
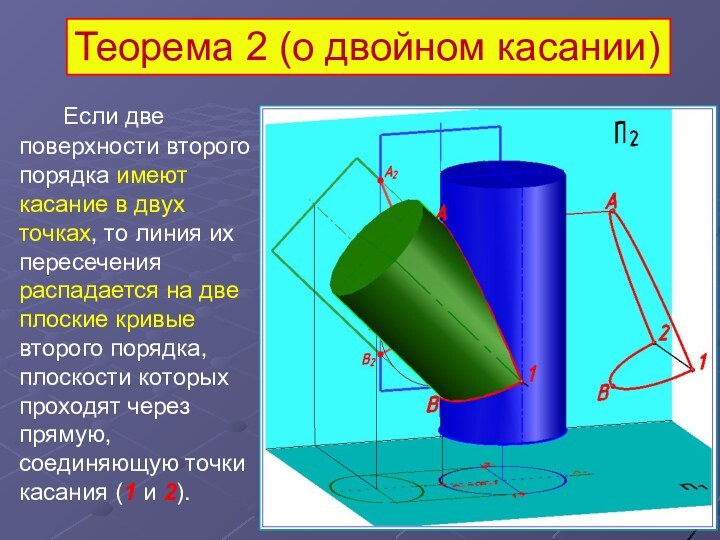
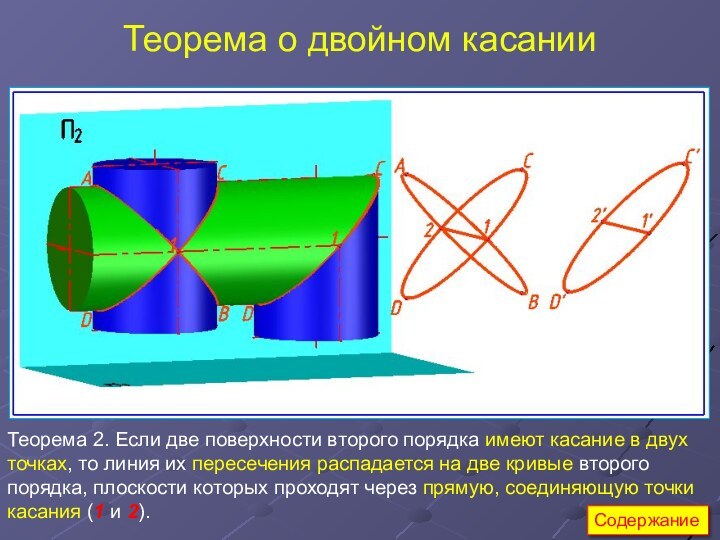
Если две поверхности второго порядка
имеют касание в двух точках, то линия их пересечения
распадается на две плоские кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки касания (1 и 2).
Теорема 2 (о двойном касании)
Слайд 14
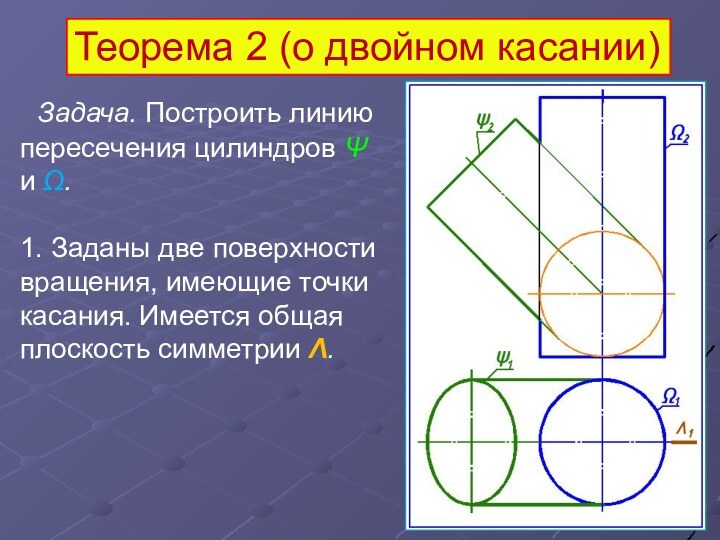
Задача. Построить линию пересечения цилиндров Ψ
и
Ω.
1. Заданы две поверхности вращения, имеющие точки касания.
Имеется общая плоскость симметрии Λ.
Теорема 2 (о двойном касании)
Слайд 15
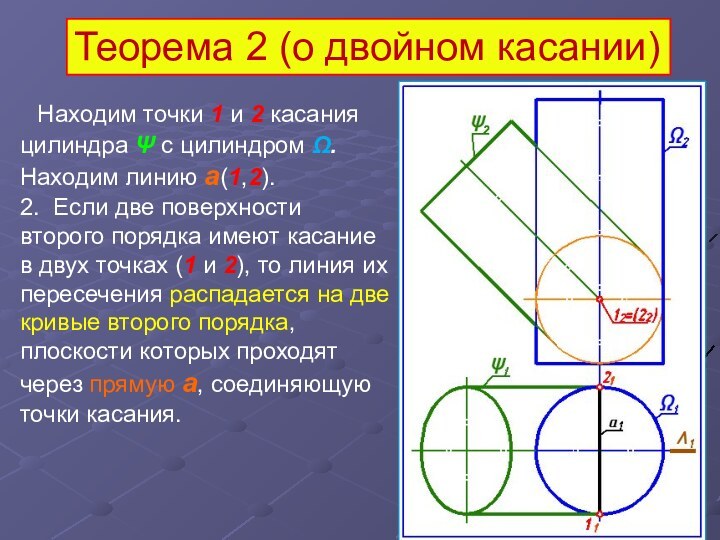
Находим точки 1 и 2 касания цилиндра
Ψ c цилиндром Ω. Находим линию а(1,2).
2. Если
две поверхности второго порядка имеют касание в двух точках (1 и 2), то линия их пересечения распадается на две кривые второго порядка, плоскости которых проходят через прямую а, соединяющую точки касания.
Теорема 2 (о двойном касании)
Слайд 16
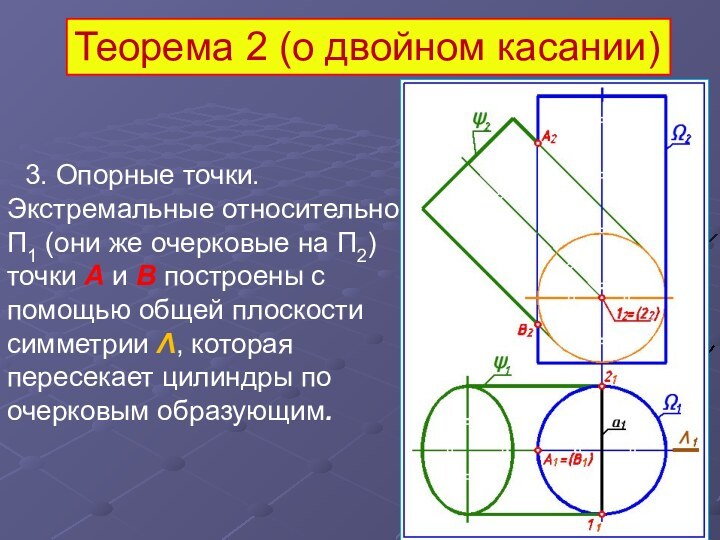
3. Опорные точки. Экстремальные относительно П1 (они
же очерковые на П2) точки A и B построены
с помощью общей плоскости симметрии Λ, которая пересекает цилиндры по очерковым образующим.
Теорема 2 (о двойном касании)
Слайд 17
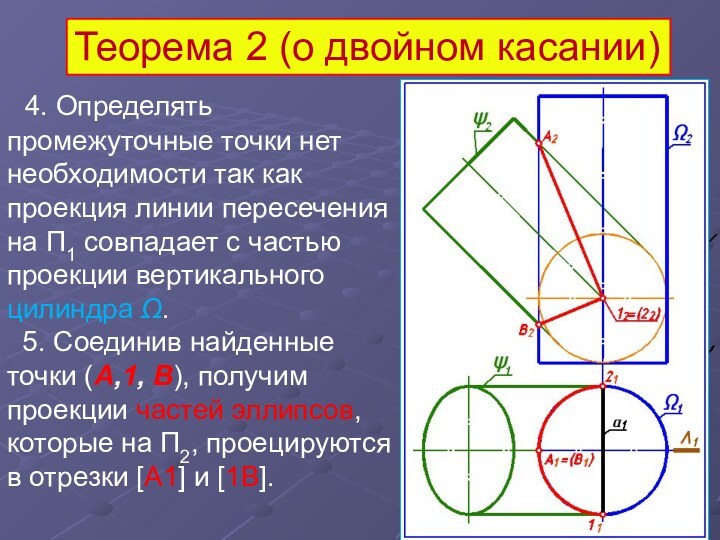
4. Определять промежуточные точки нет необходимости так
как проекция линии пересечения на П1 совпадает с частью
проекции вертикального цилиндра Ω.
5. Соединив найденные точки (А,1, В), получим проекции частей эллипсов, которые на П2, проецируются в отрезки [A1] и [1B].
Теорема 2 (о двойном касании)
Слайд 18
Теорема Монжа
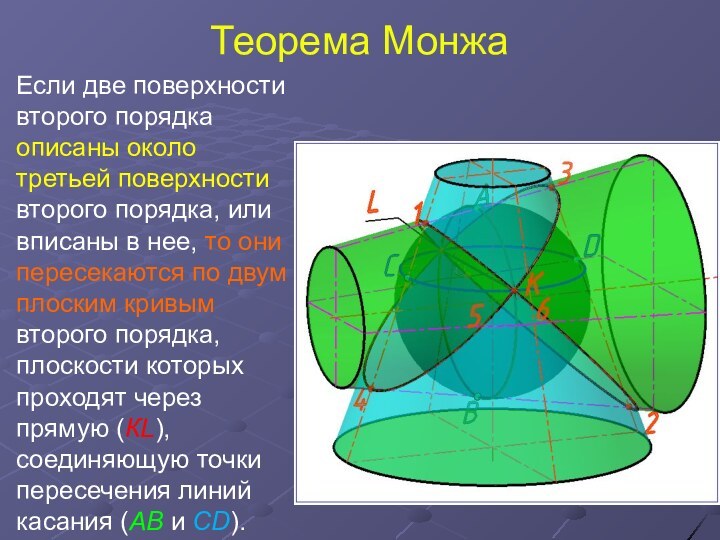
Если две поверхности второго порядка описаны около
третьей поверхности второго порядка, или вписаны в нее, то
они пересекаются по двум плоским кривым второго порядка, плоскости которых проходят через прямую (КL), соединяющую точки пересечения линий касания (AB и CD).
Слайд 19
Теорема Монжа
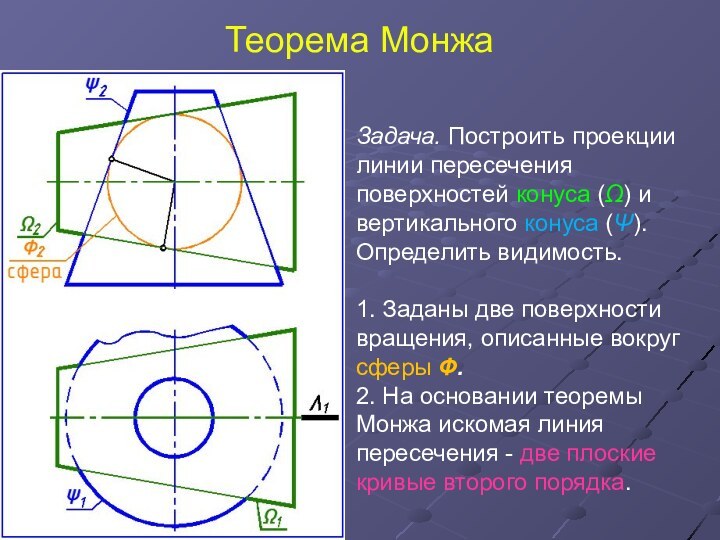
Задача. Построить проекции линии пересечения поверхностей конуса
(Ω) и вертикального конуса (Ψ). Определить видимость.
1. Заданы две
поверхности вращения, описанные вокруг сферы Ф.
2. На основании теоремы Монжа искомая линия пересечения - две плоские кривые второго порядка.
Слайд 20
Теорема Монжа
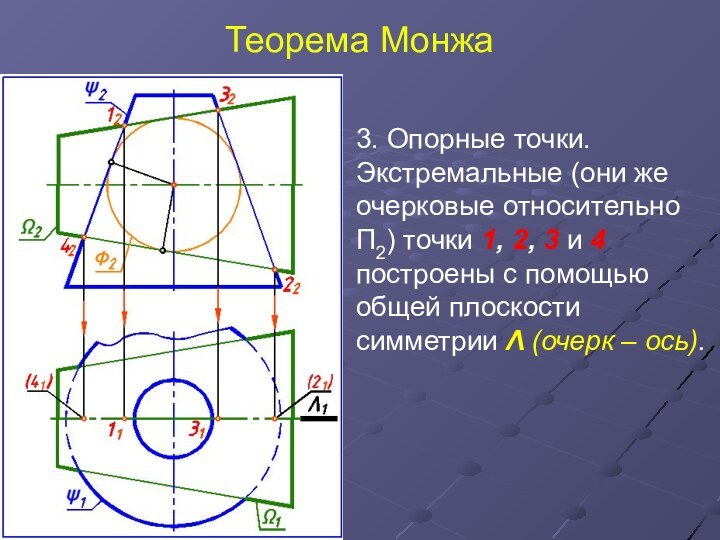
3. Опорные точки. Экстремальные (они же очерковые
относительно П2) точки 1, 2, 3 и 4 построены
с помощью общей плоскости симметрии Λ (очерк – ось).
Слайд 21
Теорема Монжа
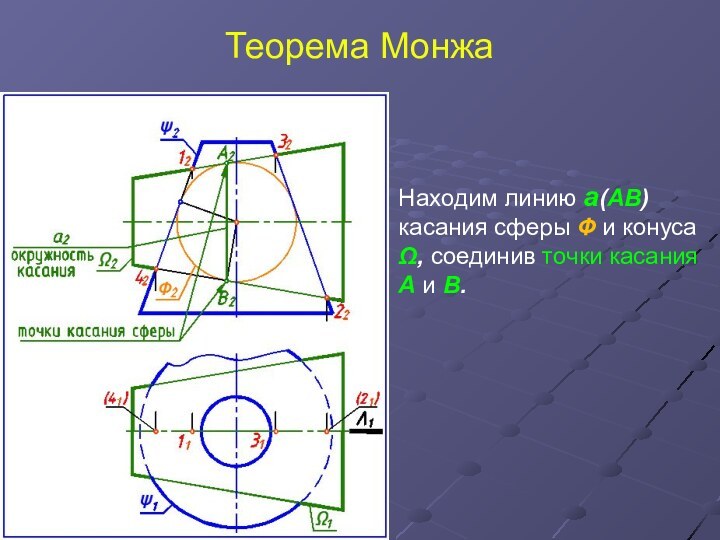
Находим линию а(АВ) касания сферы Ф и
конуса Ω, соединив точки касания А и В.
Слайд 22
Теорема Монжа
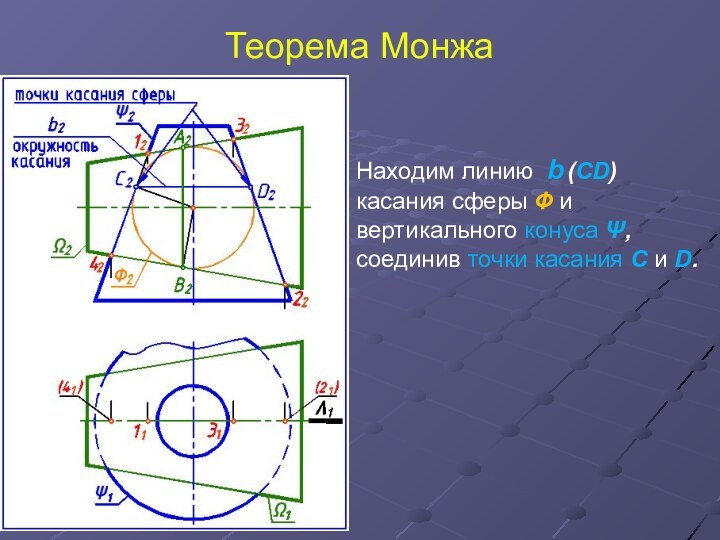
Находим линию b (СD) касания сферы Ф
и вертикального конуса Ψ, соединив точки касания С и
D.
Слайд 23
Теорема Монжа
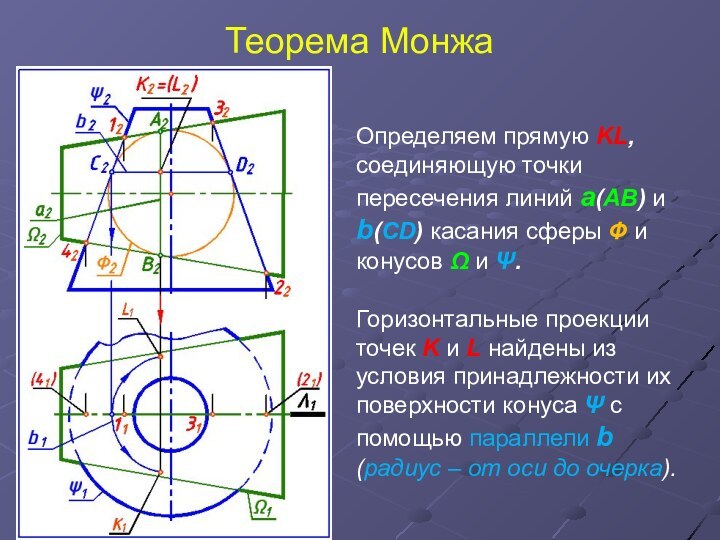
Определяем прямую KL, соединяющую точки пересечения линий
а(АВ) и b(СD) касания сферы Ф и конусов Ω
и Ψ.
Горизонтальные проекции точек K и L найдены из условия принадлежности их поверхности конуса Ψ с помощью параллели b
(радиус – от оси до очерка).
Слайд 24
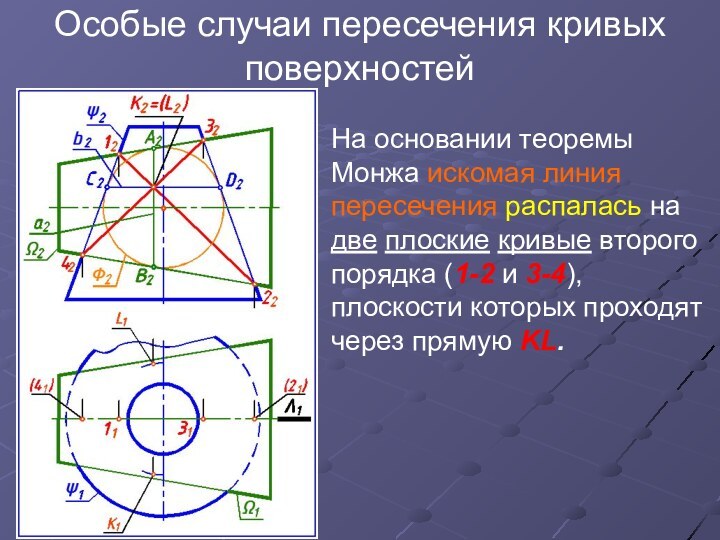
Особые случаи пересечения кривых поверхностей
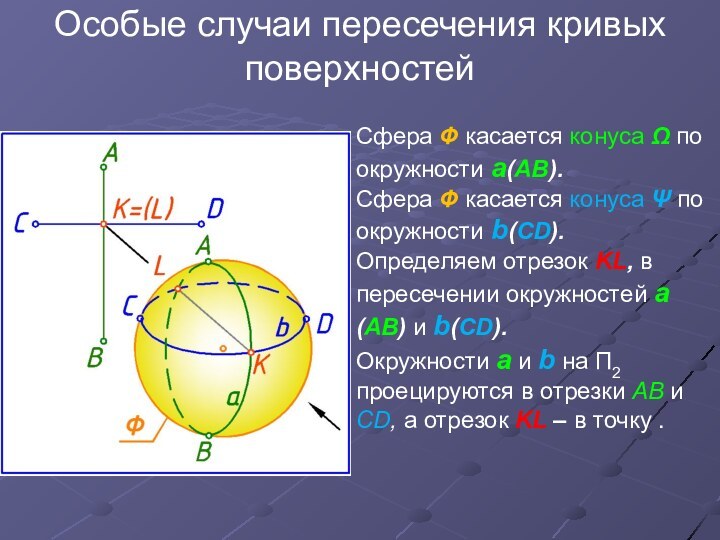
Сфера Ф касается конуса
Ω по окружности а(АВ).
Сфера Ф касается конуса Ψ
по окружности b(СD).
Определяем отрезок KL, в пересечении окружностей а(АВ) и b(СD).
Окружности а и b на П2 проецируются в отрезки АВ и СD, а отрезок KL – в точку .
Слайд 25
Особые случаи пересечения кривых поверхностей
На основании теоремы Монжа
искомая линия пересечения распалась на две плоские кривые второго
порядка (1-2 и 3-4), плоскости которых проходят через прямую KL.
Слайд 26
Теорема Монжа
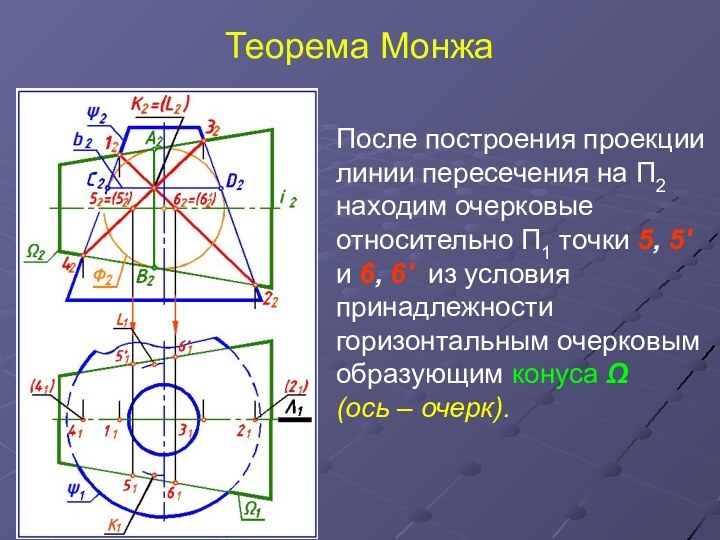
После построения проекции линии пересечения на П2
находим очерковые относительно П1 точки 5, 5' и 6,
6' из условия принадлежности горизонтальным очерковым образующим конуса Ω
(ось – очерк).
Слайд 27
Теорема Монжа
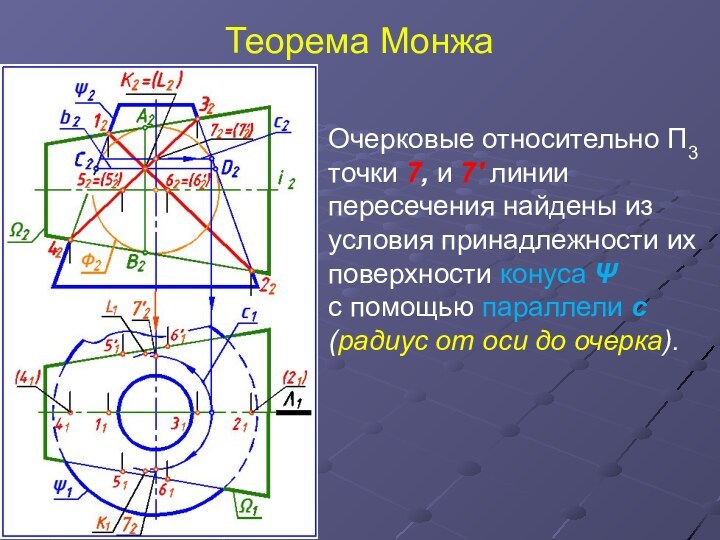
Очерковые относительно П3 точки 7, и 7'
линии пересечения найдены из условия принадлежности их поверхности конуса
Ψ
с помощью параллели с
(радиус от оси до очерка).
Слайд 28
Теорема Монжа
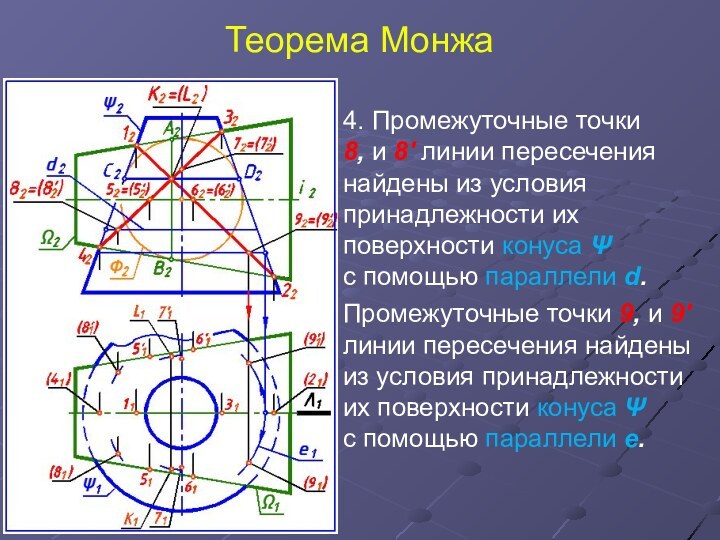
4. Промежуточные точки
8, и 8' линии пересечения
найдены из условия принадлежности их поверхности конуса Ψ
с
помощью параллели d.
Промежуточные точки 9, и 9' линии пересечения найдены из условия принадлежности их поверхности конуса Ψ
с помощью параллели e.
Слайд 29
Теорема Монжа
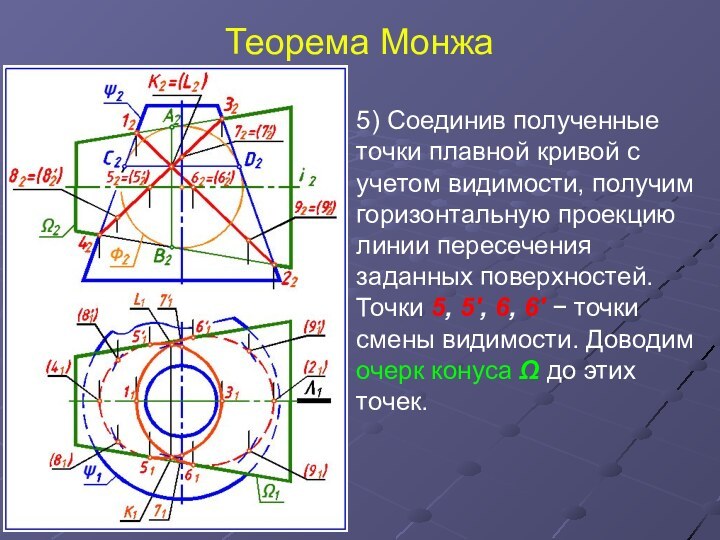
5) Соединив полученные точки плавной кривой с
учетом видимости, получим горизонтальную проекцию линии пересечения заданных поверхностей.
Точки 5, 5', 6, 6' точки смены видимости. Доводим очерк конуса Ω до этих точек.
Слайд 30
Теорема Монжа
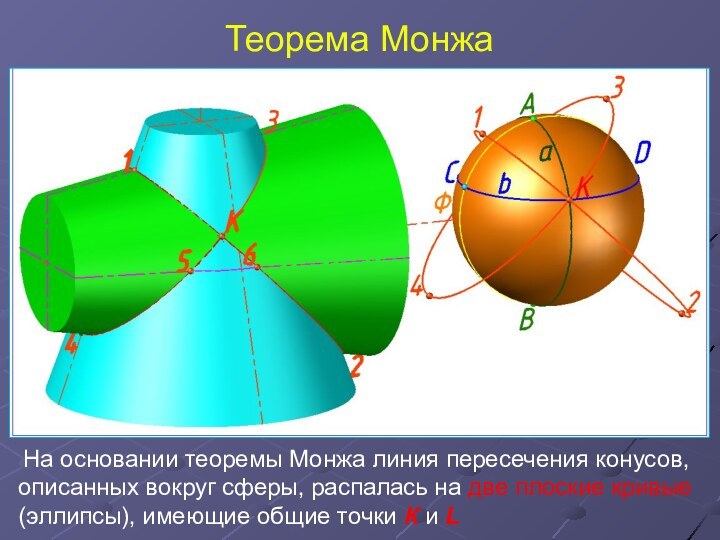
На основании теоремы Монжа линия пересечения
конусов, описанных вокруг сферы, распалась на две плоские кривые
(эллипсы), имеющие общие точки К и L
Слайд 31
Теорема о двойном касании
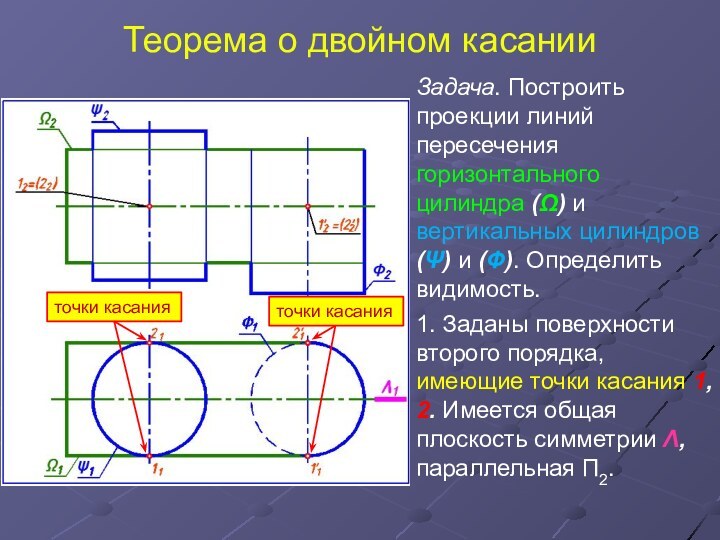
Задача. Построить проекции линий пересечения
горизонтального цилиндра (Ω) и вертикальных цилиндров (Ψ) и (Ф).
Определить видимость.
1. Заданы поверхности второго порядка, имеющие точки касания 1, 2. Имеется общая плоскость симметрии Λ, параллельная П2.
Слайд 32
Теорема о двойном касании
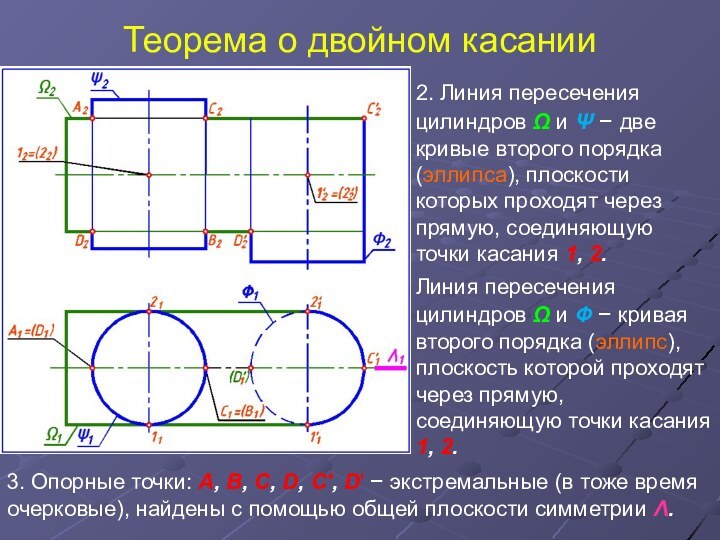
2. Линия пересечения цилиндров Ω
и Ψ две кривые второго порядка (эллипса), плоскости
которых проходят через прямую, соединяющую точки касания 1, 2.
Линия пересечения цилиндров Ω и Ф кривая второго порядка (эллипс), плоскость которой проходят через прямую, соединяющую точки касания 1, 2.
3. Опорные точки: A, B, C, D, C', D' экстремальные (в тоже время очерковые), найдены с помощью общей плоскости симметрии Λ.
Слайд 33
Теорема о двойном касании
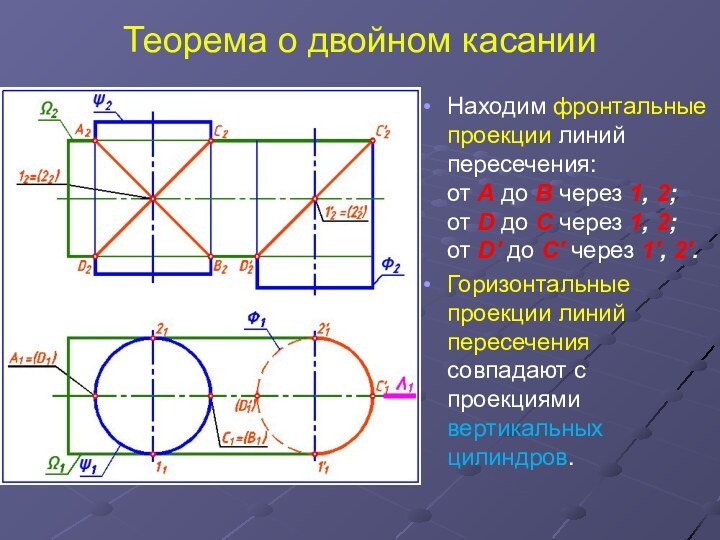
Находим фронтальные проекции линий пересечения:
от А до В через 1, 2;
от D до
C через 1, 2;
от D' до C' через 1', 2'.
Горизонтальные проекции линий пересечения совпадают с проекциями вертикальных цилиндров.