- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Оценка статистической значимости коэффициентов регрессии и уравнения в целом
Содержание
- 2. Большинство эконометрических моделей требуют многократного улучшения и
- 3. анализом качества найденных оценок; достоверностью полученных
- 4. Статистической называют гипотезу о виде закона распределения
- 5. Гипотеза Н0, подлежащая проверке, называется нулевой (основной).
- 6. Такая гипотеза называется альтернативной (конкурирующей). Сущность проверки
- 7. Эта задача решается с помощью специальных методов математической статистики – методов статистической проверки гипотез.
- 8. При проверке гипотезы выборочные данные могут противоречить
- 9. Статистическая проверка гипотез на основании выборочных данных
- 10. Ошибка первого рода состоит в том, что
- 12. Последствия указанных ошибок неравнозначны. Первая приводит к
- 13. Например, если Н0 состоит в признании продукции
- 14. Очевидно, последствия второй ошибки более серьезны с
- 15. Исключить ошибки первого и второго рода невозможно
- 16. При этом одновременное уменьшение вероятностей данных ошибок
- 17. Вероятность совершить ошибку первого рода принято обозначать буквой α, и ее называют уровнем значимости.
- 18. Обычно значения α задают заранее (например, 0,1;
- 19. Проверку статистической гипотезы осуществляют на основании данных
- 20. t - случайная величина распределена по закону Стьюдента;F - случайная величина распределена по закону Фишера.
- 21. После выбора определенного критерия множество всех его возможных значений разбивают на два непересекающихся подмножества:
- 22. 2. содержит значения критерия, при
- 23. Совокупность значений критерия, при которых нулевую гипотезу
- 24. Основной принцип проверки статистических гипотез можно сформулировать так:
- 25. если наблюдаемое значение критерия (вычисленное по
- 26. Точки, разделяющие критическую область и область принятия
- 27. Общая схема проверки гипотез:3. Выбор критерия для
- 28. 6. Принятие статистического решения.5. Вычисление наблюдаемого значения (фактического) критерия.4. Определение критической области и области принятия гипотезы.
- 29. Эмпирическое уравнение регрессии определяется на основе конечного
- 30. При проведении статистического анализа перед исследователем возникает
- 31. Выдвигается ноль-гипотеза:Альтернативная гипотеза:коэффициент регрессии статистически незначимкоэффициент регрессии статистически значим
- 32. Статистическая значимость коэффициента регрессии проверяется с помощью t-критерия Стьюдента.
- 33. Для этого сначала необходимо определить остаточную сумму квадратов:
- 34. Ее среднее квадратическое отклонение:
- 35. Затем определяется стандартная ошибка коэффициента регрессии
- 36. Фактическое значение t-критерия Стьюдента для коэффициента регрессии рассчитывается как:
- 37. Критическое значение t-статистики определяется из таблицы распределения
- 38. Если tb>tкр, то нулевая гипотеза отвергается и
- 39. В противном случае, говорят, что «нет оснований отвергать нулевую гипотезу»: коэффициент регрессии статистически незначим.
- 40. По аналогичной схеме на основании t-статистики проверяется гипотеза о статистической значимости коэффициента а.
- 41. Для парной регрессии более важным является анализ
- 42. Можно построить доверительный интервал для b:
- 43. Доверительный интервал накрывает истинное значение параметра b
- 44. Оценка статистической значимости постороенной модели регрессии в
- 45. Соответственно, альтернативная гипотеза - коэффициент детерминации статистически значим:
- 46. Фактическое значение F-критерия для уравнения парной регрессии, линейной по параметрам определяется как:
- 47. Фактическое значение сравнивается с табличным значением случайной
- 48. Скачать презентацию
- 49. Похожие презентации
Большинство эконометрических моделей требуют многократного улучшения и уточнения. Для этого необходимо проведение соответствующих расчетов, связанных: с установлением выполнимости или невыполнимости тех или иных предпосылок;





























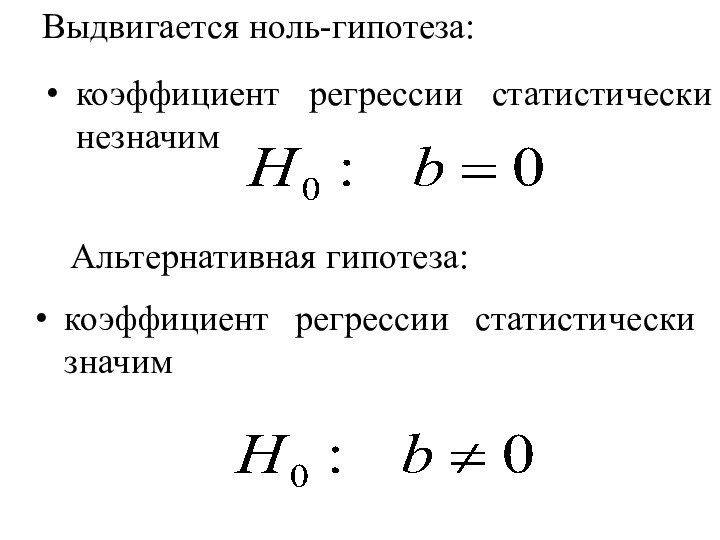










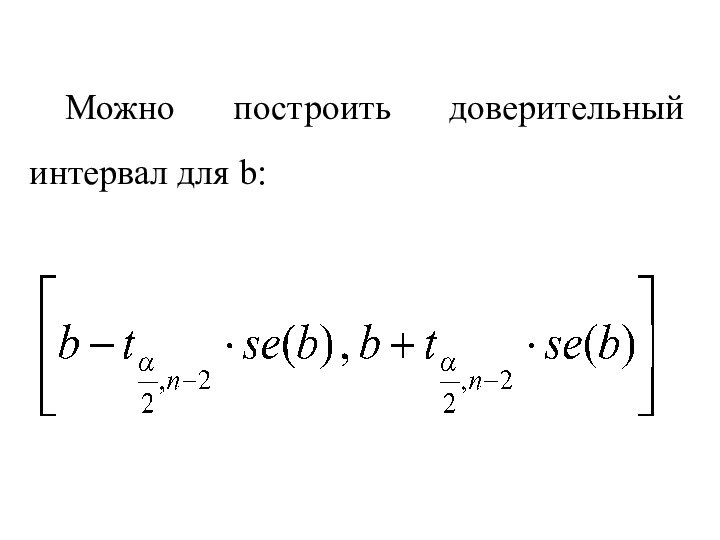


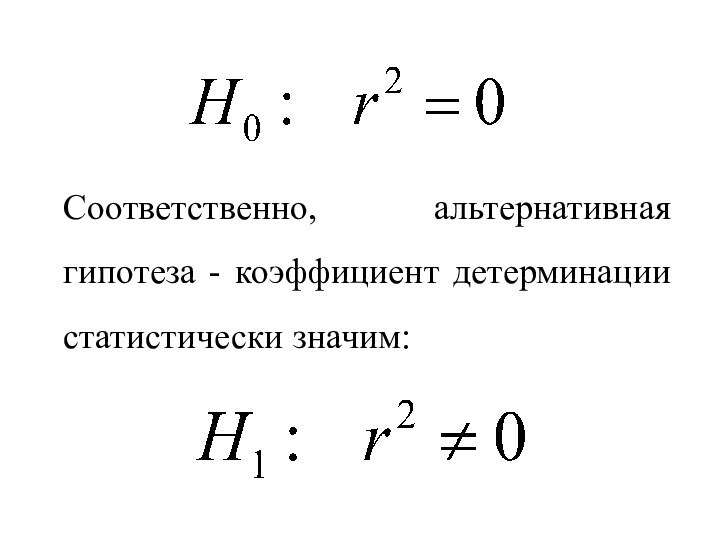



Слайд 2 Большинство эконометрических моделей требуют многократного улучшения и уточнения.
выполнимости или невыполнимости тех или иных предпосылок;
Слайд 3
анализом качества найденных оценок;
достоверностью полученных выводов.
Обычно эти расчеты проводятся по схеме статистической проверки гипотез.
Слайд 4 Статистической называют гипотезу о виде закона распределения или
о параметрах известного распределения.
В первом случае гипотеза называется
непараметрической, а во втором – параметрической.
Слайд 5
Гипотеза Н0, подлежащая проверке, называется нулевой (основной).
Наряду
с нулевой рассматривают гипотезу Н1, которая будет приниматься, если
отклоняется Н0.
Слайд 6
Такая гипотеза называется альтернативной (конкурирующей).
Сущность проверки статистической
гипотезы заключается в том, чтобы установить, согласуются или нет
данные наблюдений и выдвинутая гипотеза.Слайд 7 Эта задача решается с помощью специальных методов математической
статистики – методов статистической проверки гипотез.
Слайд 8 При проверке гипотезы выборочные данные могут противоречить гипотезе
Н0. Тогда она отклоняется.
Если же статистические данные согласуются
с выдвинутой гипотезой, то она не отклоняется. Слайд 9 Статистическая проверка гипотез на основании выборочных данных неизбежно
связана с риском принятия ложного решения.
При этом возможны ошибки
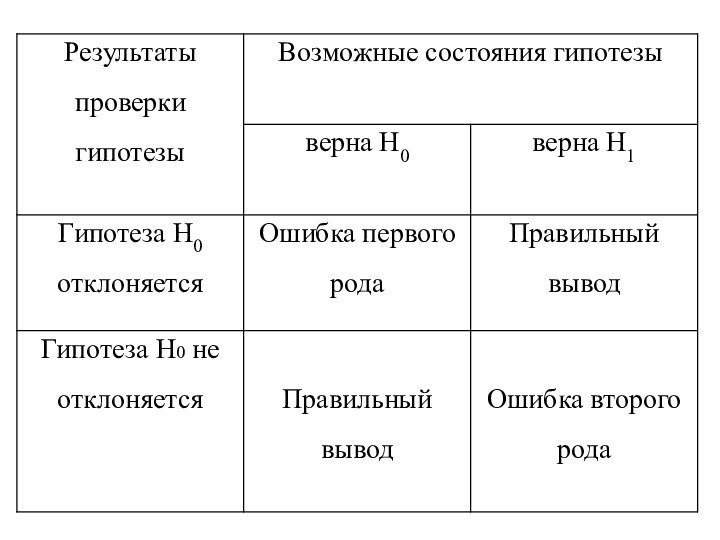
двух родов.Слайд 10 Ошибка первого рода состоит в том, что будет
отвергнута правильная нулевая гипотеза.
Ошибка второго рода состоит в том,
что будет принята нулевая гипотеза, в то время как в действительности верна альтернативная гипотеза.
Слайд 12
Последствия указанных ошибок неравнозначны.
Первая приводит к более
осторожному, консервативному решению, вторая – к неоправданному риску.
Что
лучше или хуже – зависит от конкретной постановки задачи и содержания нулевой гипотезы.Слайд 13 Например, если Н0 состоит в признании продукции предприятия
качественной и допущена ошибка первого рода, то будет забракована
годная продукция.Слайд 14 Очевидно, последствия второй ошибки более серьезны с точки
зрения имиджа фирмы и ее долгосрочных перспектив.
Допустив ошибку второго
рода, мы отправим потребителю брак. Слайд 15 Исключить ошибки первого и второго рода невозможно в
силу ограниченности выборки.
Поэтому стремятся минимизировать потери от этих
ошибок. Слайд 16 При этом одновременное уменьшение вероятностей данных ошибок невозможно,
так как задачи их уменьшения являются конкурирующими.
Снижение вероятности
допустить одну из них влечет за собой увеличение вероятности допустить другую. Слайд 17 Вероятность совершить ошибку первого рода принято обозначать буквой
α, и ее называют уровнем значимости.
Слайд 18 Обычно значения α задают заранее (например, 0,1; 0,05;
0,01 и т.д.)
Если α = 0,05, то это означает,
что исследователь не хочет совершить ошибку первого рода более чем в 5 случаях из 100.Слайд 19 Проверку статистической гипотезы осуществляют на основании данных выборки.
Для этого используют специально подобранную случайную величину (статистику, критерий),
точное или приближенное значение которой известно.
Слайд 20
t - случайная величина распределена по закону Стьюдента;
F
- случайная величина распределена
по закону Фишера.
Слайд 21 После выбора определенного критерия множество всех его возможных
значений разбивают на два непересекающихся подмножества:
Слайд 22 2. содержит значения критерия, при
которых она не отклоняется.
содержит значения критерия, при которых нулевая гипотеза отклоняется
Слайд 23 Совокупность значений критерия, при которых нулевую гипотезу отклоняют,
называют критической областью.
Совокупность значений критерия, при которых нулевую
гипотезу не отклоняют, называют областью принятия гипотезы.Слайд 25 если наблюдаемое значение критерия (вычисленное по выборке)
принадлежит критической области, то нулевую гипотезу отклоняют.
если же наблюдаемое
значение критерияпринадлежит области принятия гипотезы, то нулевую гипотезу не отклоняют.
Слайд 26 Точки, разделяющие критическую область и область принятия гипотезы,
называют критическими.
В основу определения критических точек
и критической области
положен принциппрактической невозможности
маловероятных событий.
Слайд 27
Общая схема проверки гипотез:
3. Выбор критерия для проверки
Н0.
2. Выбор соответствующего уровня значимости α.
1. Формулировка проверяемой (нулевой
– Н0) и альтернативной (Н1) гипотез.
Слайд 28
6. Принятие статистического решения.
5. Вычисление наблюдаемого значения (фактического)
критерия.
4. Определение критической области и области принятия гипотезы.
Слайд 29 Эмпирическое уравнение регрессии определяется на основе конечного числа
статистических данных.
Коэффициенты эмпирического уравнения регрессии являются случайными величинами,
изменяющимися от выборки к выборке. Слайд 30 При проведении статистического анализа перед исследователем возникает необходимость
сравнения эмпирических коэффициентов регрессии a и b с некоторыми
теоретически ожидаемыми значениями α и β этих коэффициентов.
Слайд 31
Выдвигается ноль-гипотеза:
Альтернативная гипотеза:
коэффициент регрессии статистически незначим
коэффициент регрессии статистически
значим
Слайд 32 Статистическая значимость коэффициента регрессии проверяется с помощью t-критерия
Стьюдента.
Слайд 37 Критическое значение t-статистики определяется из таблицы распределения данной
случайной величины при заданном уровне значимости α и числе
степеней свободы (n-2), где n – размер выборки.Слайд 38 Если tb>tкр, то нулевая гипотеза отвергается и принимается
альтернативная гипотеза о статистической значимости коэффициента регрессии с вероятностью
(1- α)
Слайд 39
В противном случае, говорят, что
«нет оснований
отвергать нулевую гипотезу»: коэффициент регрессии статистически незначим.
Слайд 40
По аналогичной схеме на основании
t-статистики проверяется гипотеза
о
статистической значимости коэффициента а.
Слайд 41 Для парной регрессии более важным является анализ статистической
значимости коэффициента b, так как именно в нем скрыто
влияние объясняющей переменной Х на зависимую переменную Y.
Слайд 43
Доверительный интервал накрывает
истинное значение параметра b с
заданной
вероятностью (если α=0,05, то с
вероятностью в 95%).
Слайд 44
Оценка статистической значимости
постороенной модели регрессии в
целом
производится с помощью
F-критерия Фишера. В качестве нулевой гипотезы
используется утверждение о незначимости коэффициента детерминации: ,





























