- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ
Содержание
- 2. Параллельные плоскости в пространствеОпределение. Две плоскости в пространстве называются параллельными, еслиони не пересекаются.
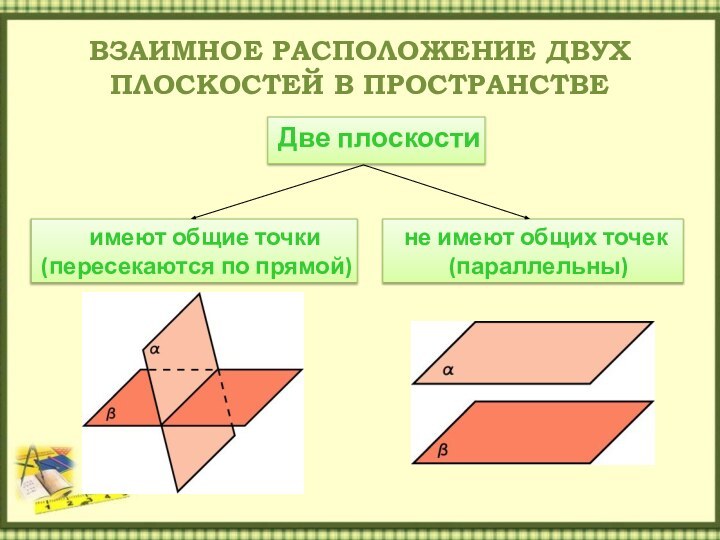
- 3. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПЛОСКОСТЕЙ В ПРОСТРАНСТВЕ
- 4. Признак параллельности плоскостей Теорема1. Если две пересекающиеся прямые
- 5. О СВОЙСТВЕ ПРОТИВОЛЕЖАЩИХ ГРАНЕЙ ПАРАЛЛЕЛЕПИПЕДАТеорема2. Противолежащие грани параллелепипеда лежат в параллельных плоскостях
- 6. О прямых пересечения двух параллельных плоскостей третьей
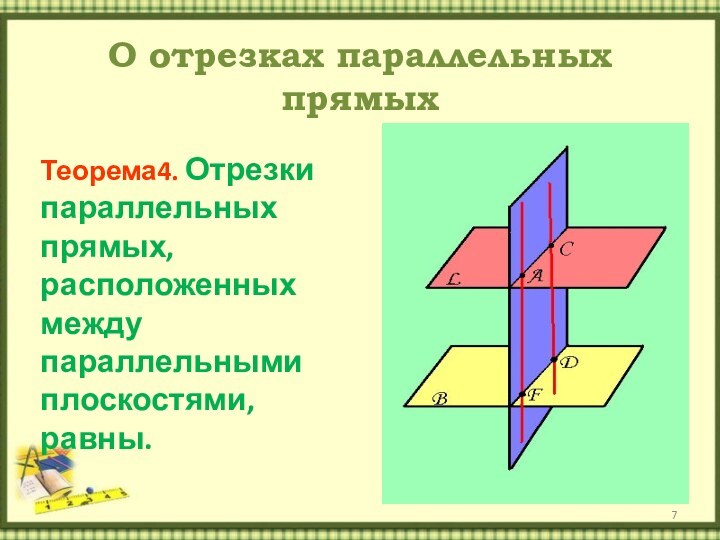
- 7. О отрезках параллельных прямыхТеорема4. Отрезки параллельных прямых, расположенных между параллельными плоскостями, равны.
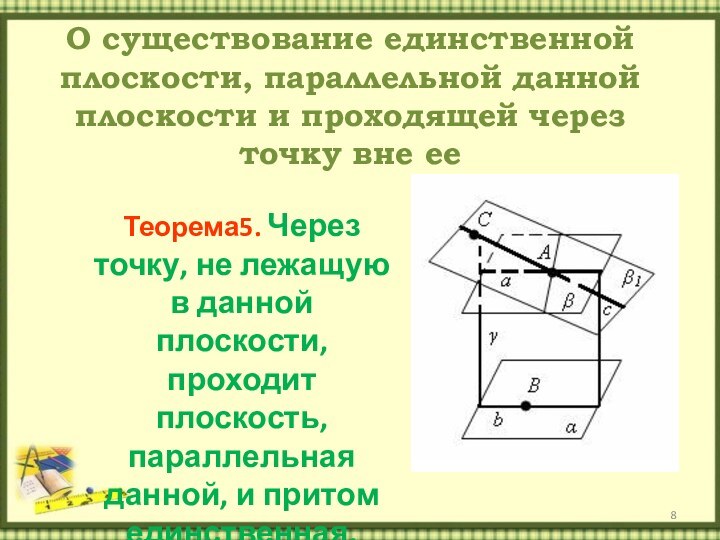
- 8. О существование единственной плоскости, параллельной данной плоскости
- 9. Задачи для обсуждения:1. Точки Р,Т и Е
- 10. 2. АВСА1В1С1 – правильная треугольная призма, каждое
- 11. 3. Докажите, что через две скрещивающиеся прямые
- 12. Проверка усвоенного: 1.Можно ли признак параллельности двух
- 13. Нет
- 14. 2. Верно ли утверждение, что если через
- 15. Нет
- 16. 3. Можно ли две параллельные плоскости пересечь третьей плоскостью по двум непараллельным прямым?
- 17. Нет
- 18. 4. Можно ли две пересекающиеся плоскости пересечь третьей плоскостью по параллельным прямым?
- 19. Да
- 20. 5. Сколько можно провести через данную точку плоскостей, параллельных данной плоскости?
- 21. Одну
- 22. Скачать презентацию
- 23. Похожие презентации
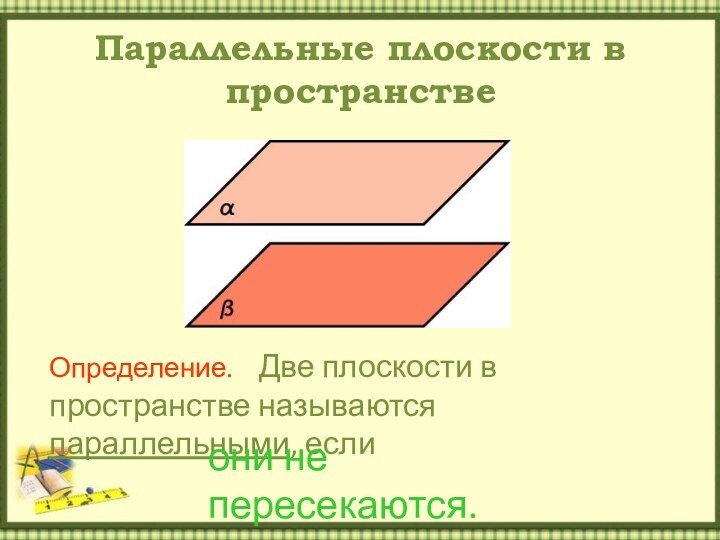
Параллельные плоскости в пространствеОпределение. Две плоскости в пространстве называются параллельными, еслиони не пересекаются.
















Слайд 2
Параллельные плоскости в пространстве
Определение. Две плоскости в
пространстве называются параллельными, если
Слайд 4
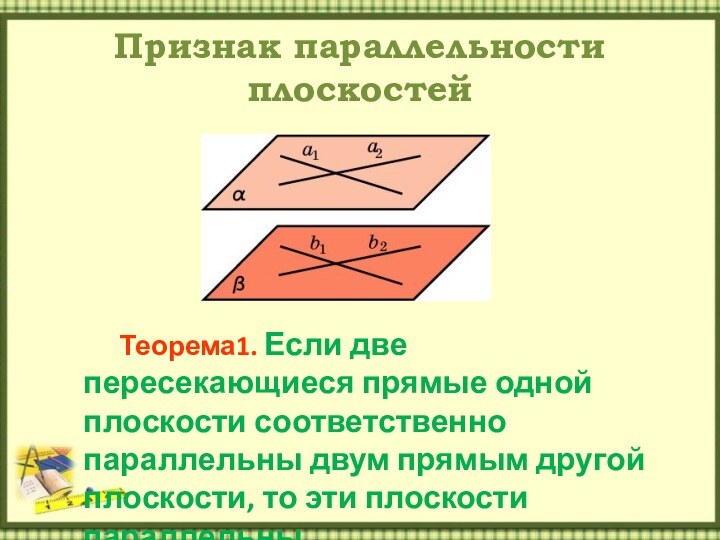
Признак параллельности плоскостей
Теорема1. Если две пересекающиеся прямые одной
плоскости соответственно параллельны двум прямым другой плоскости, то эти
плоскости параллельны.
Слайд 5
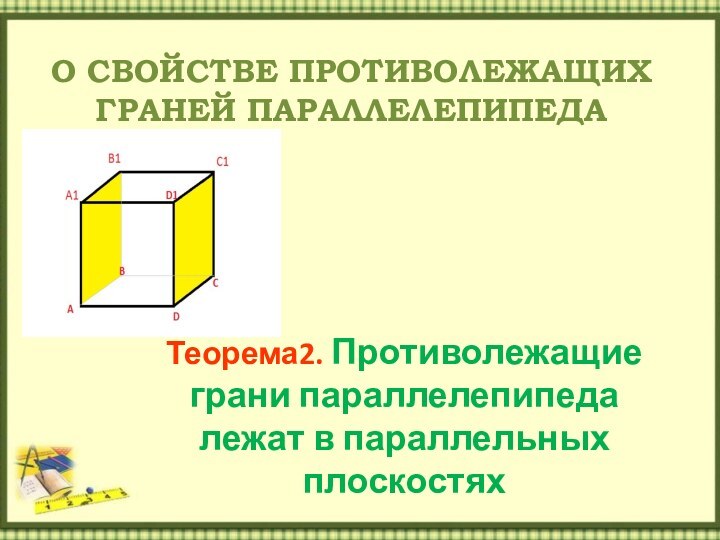
О СВОЙСТВЕ ПРОТИВОЛЕЖАЩИХ ГРАНЕЙ ПАРАЛЛЕЛЕПИПЕДА
Теорема2. Противолежащие грани параллелепипеда
лежат в параллельных плоскостях
Слайд 6
О прямых пересечения двух параллельных плоскостей третьей плоскостью
Теорема3.
Если две параллельных плоскости пересечены третьей, то прямые их
пересечения параллельны между собой.а
в
у
а
в














![Рекомендации для родителей в логопедический уголок. Звуки [Б], [Б']. Буква Б. методическая разработка](/img/tmb/9/842724/d55704f4c812b05f1c21858f2efe1ca7-210x.jpg)














