Слайд 2
План
Аксиома параллельности
Пятый постулат Евклида
Признаки параллельности прямых на плоскости
Пересечение
сторон угла ||-ми прямыми
Параллельные прямые в пространстве
Скрещивающиеся прямые
Параллельность прямой
и плоскости
Параллельность плоскостей
Свойства параллельных плоскостей
Слайд 3
Аксиома параллельности
прямых
Определение. Две прямые на плоскости называются параллельными,
если они не пересекаются.
Аксиома
Через точку, не лежащую на данной
прямой, можно провести на плоскости не более одной прямой, параллельной данной.
Выучите ее.
Слайд 4
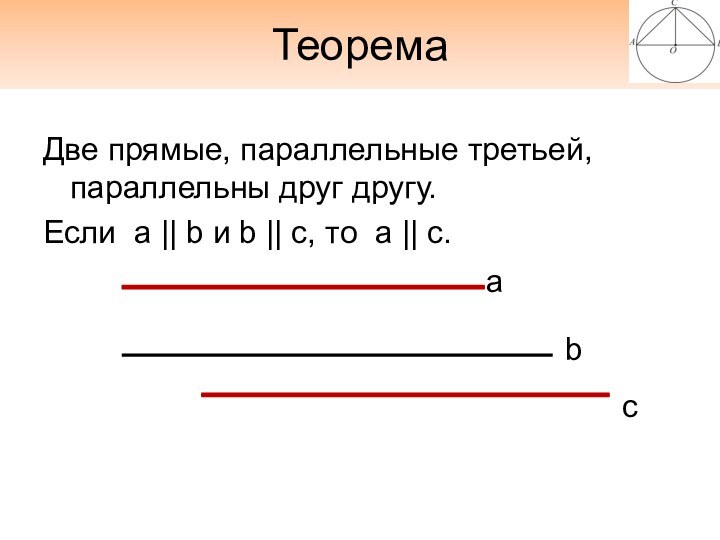
Теорема
Две прямые, параллельные третьей, параллельны друг другу.
Если a
|| b и b || c, то a ||
c.
a
c
b
Слайд 5
Сопоставляя предыдущее утверждение и аксиому параллельных, приходят к
важному выводу:
На плоскости через точку, не лежащую на данной
прямой, можно провести параллельную ей прямую, и только одну.
Слайд 6
Пятый постулат
Аксиома параллельности в книге Евклида «Начала» эквивалентна
так называемому пятому постулату.
Если две прямые пересекаются третьей
так, что по какую-либо сторону от нее сумма внутренних углов меньше двух прямых углов, то по эту же сторону исходные прямые пересекаются.
Слайд 7
Геометрия Лобачевского
Пятый постулат Евклида в отличие от других
аксиом Евклида менее очевиден, и в течение 2000 лет
многие математики безуспешно пытались вывести его из других аксиом Евклида.
А также пытались доказать единственность параллельной.
В 1826 г. Николай Иванович Лобачевский в Казанском университете представил доклад о новой геометрии, которую он назвал воображаемой геометрией.
Слайд 8
Система аксиом геометрии Лобачевского получается из системы аксиом
геометрии Евклида простой заменой пятого постулата аксиомой Лобачевского:
Перпендикуляр и
наклонная,
проведенные в плоскости к
одной прямой, могут не
пересекаться.
Слайд 9
Псевдосфера
В евклидовом простран-
стве имеется поверхность,
на которой кратчайшие
линии ведут
себя как
прямые на плоскости
Лобачевского.
(итал. математик
Бельтрами, 1868 г.)
Слайд 10
Пересечение параллель-
ных прямых третьей
Какие углы вы знаете?
Слайд 11
Углы при параллельных
и секущей
1. Соответственные: 1 = 5,
2 = 6,
3 = 7, 4 = 8.
2. Внутренние
накрест лежащие углы
4 = 5, 3 = 6.
3. Внешние накрест лежащие углы
1 = 8, 2 = 7.
Слайд 12
4. Внутренние односторонние углы в сумме составляют 180:
3
+ 5 = 180, 4 + 6 = 180.
5.
Внешние односторонние углы в сумме составляют 180:
1 + 7 = 180, 2 + 8 = 180.
Слайд 13
Теорема об углах с соответственно
параллельными сторонами
Углы с соответственно параллельными сторонами
либо равны друг другу (если они оба острые или оба тупые), либо в сумме дают 180.
1 = 2 3 + 4 = 180
Слайд 14
Признаки параллельности прямых
Две прямые на плоскости параллельны в
том и только том случае, если при пересечении их
секущей
внутренние накрест лежащие углы равны;
сумма внутренних
односторонних углов
равна 180.
Слайд 15
Теорема о пересечении сторон
угла параллельными прямыми
При пересечении сторон
угла параллельными прямыми на сторонах угла отсекаются пропорциональные отрезки.
Слайд 21
Краткая формулировка
теоремы Фалеса
Параллельные прямые отсекают на сторонах угла
пропорциональные отрезки
Слайд 22
Практическая задача
Как разделить данный отрезок на 5 равных
частей, используя циркуль и линейку без делений?
Слайд 23
Аналогичная задача
Как разделить с помощью циркуля и линейки
данный отрезок в отношении
1 : 2 (или 3
: 4)?
Слайд 24
Параллельные прямые в пространстве
Две прямые в пр-ве наз.
параллельными, если они лежат в одной плоскости и не
пересекаются.
Задача. Докажите,
все прямые,
пересекающие
две данные
параллельные прямые, лежат в одной плоскости.
Слайд 25
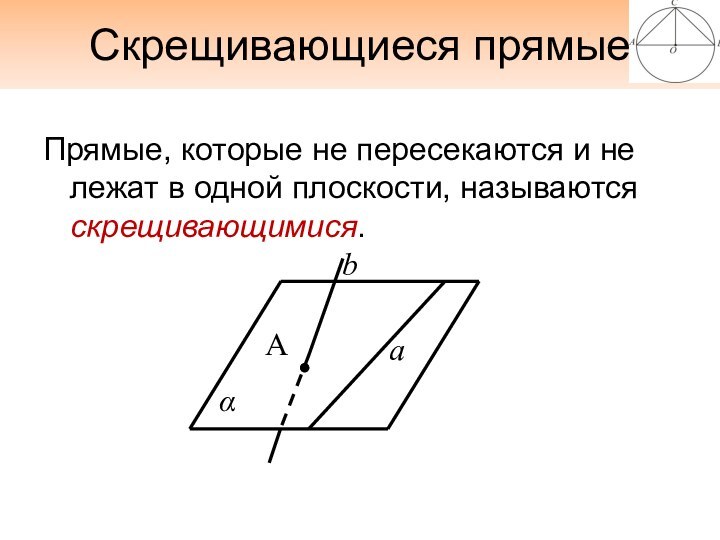
Скрещивающиеся прямые
Прямые, которые не пересекаются и не лежат
в одной плоскости, называются скрещивающимися.
Слайд 26
Теорема 1
Через точку вне данной прямой можно провести
прямую, параллельную этой прямой, и притом только одну.
(Погорелов,
стр. 239, § 16)
Дано:
а – данная прямая;
А – данная точка, не лежащая на данной прямой.
Слайд 27
Доказательство
Докажем единственность прямой а1. Допустим, что
существует другая
прямая а2,
прохо-
дящая через т. A
и параллельная
прямой a. Через прямые a
и а2 можно
провести плоскость α2.
Плоскость α2 проходит через прямую a и
т. A; сл-но, она совпадает с α. Теперь по
аксиоме параллельных прямые а1 и a2
совпадают.
Слайд 28
Признак параллельности
прямых
Теорема. Две прямые, параллельные третьей прямой, параллельны.
Дано:
прямая b || прямой а;
с || a.
Доказать: прямая b || c.
Это свойство называется транзитивностью.
b || a, a || c => b || c.
Слайд 29
Доказательство признака
При доказательстве рассмотрим два случая, когда эти
три прямые лежат в одной плоскости и не лежат.
Рассмотрим случай, когда все три прямые а, b, и с лежат в одной плоскости.
Предположим, что b и с не параллельны, тогда они пересекаются в некоторой точке. Значит, через эту точку проходят две прямые (b и с), параллельные прямой а.
Слайд 30
Но это невозможно, так как через точку, не
лежащую на данной прямой, можно провести на плоскости не
более одной прямой, параллельной данной (по аксиоме параллельных прямых). Противоречие доказывает этот случай.
Теперь рассмотрим случай, когда эти три прямые не лежат в одной плоскости.
Слайд 31
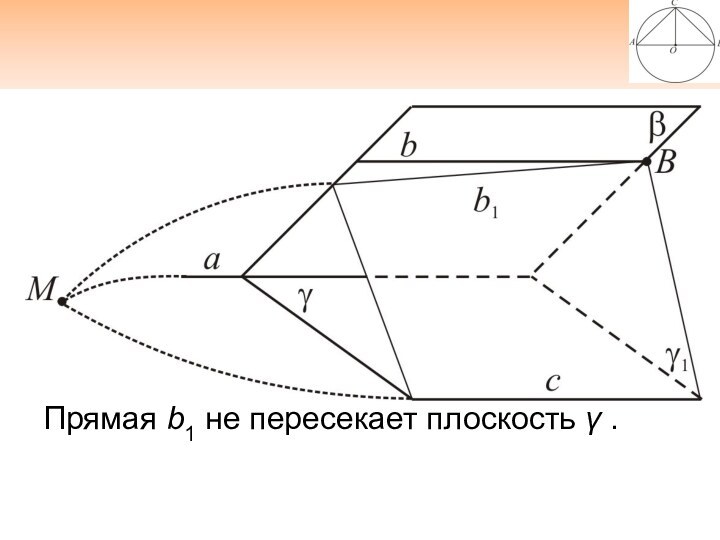
Прямая b1 не пересекает плоскость γ .
Слайд 32
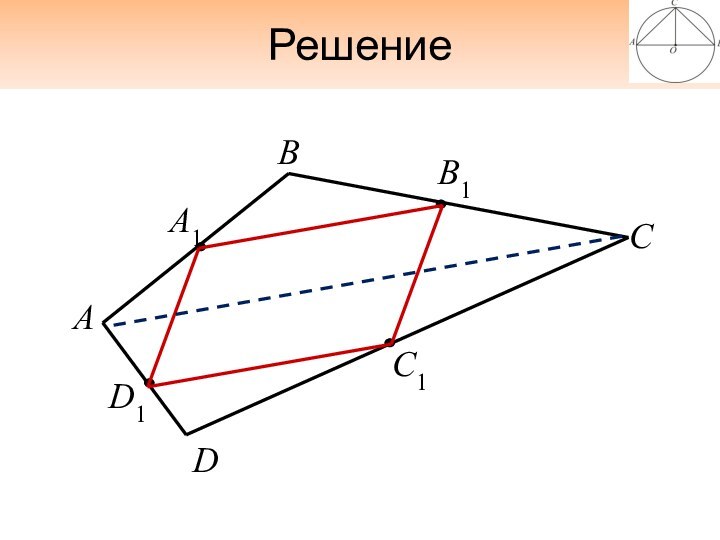
Задача
Докажите, что середины сторон пространственного четырехугольника ABCD являются
вершинами параллелограмма. (Вершины пространственного четырехугольника не лежат в одной
плоскости).
Обозначим середины сторон ABCD через A1, B1, C1, D1.
Слайд 34
Признак параллельности
прямой и плоскости
Определение. Прямая и плоскость называются
параллельными, если они не пересекаются.
Теорема. Если прямая, не принадлежащая
плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.
Слайд 35
Дано: плоскость α; прямая а пл-ти
α;
прямая а1
пл-ти α и а1 | | a.
Доказать: прямая а | | пл-ти α.
Док-во. Проведем
пл-ть α1 через
прямые а и а1.
Плоскости α и α1
пересекаются по
прямой а1.
Слайд 36
Прямая а1 лежит
одновременно в
двух плоскостях:
α и α1 .
Если бы прямая а
пересекала пл-ть α, то
точка пересечения принадлежала
бы
прямой а1. Но это невозможно, т.к. прямые
а и а1 параллельны.
Слайд 37
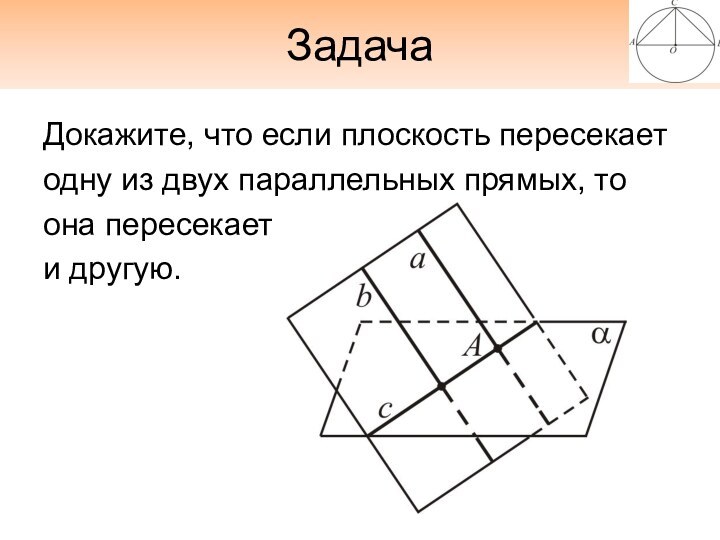
Задача
Докажите, что если плоскость пересекает
одну из двух параллельных
прямых, то
она пересекает
и другую.
Слайд 38
Признак параллельности плоскостей
Теорема. Если две пересекающиеся
прямые одной пл-ти
соот-но
параллельны
двум прямым другой
пл-ти, то эти пл-ти
параллельны.
Дано: а1 | |
b1;
a2 | | b2.
Слайд 39
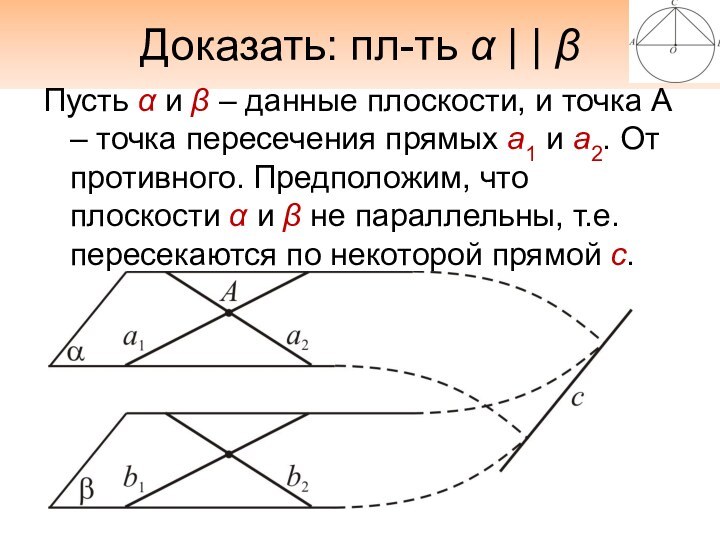
Доказать: пл-ть α | | β
Пусть α и
β – данные плоскости, и точка А – точка
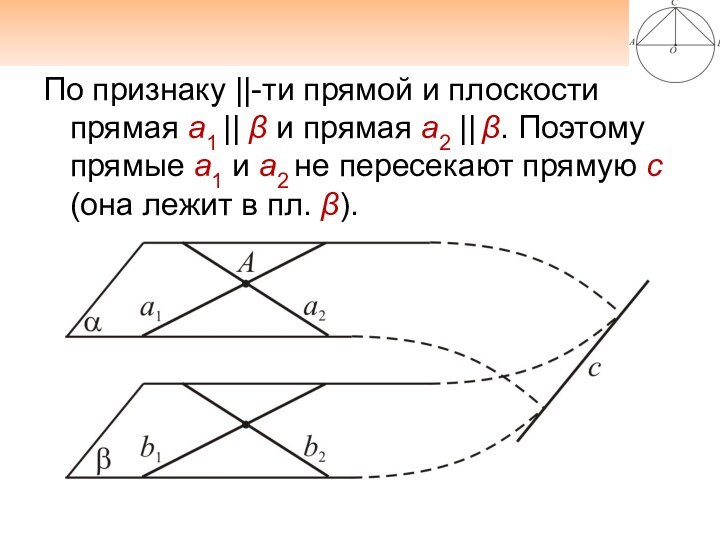
пересечения прямых а1 и а2. От противного. Предположим, что плоскости α и β не параллельны, т.е. пересекаются по некоторой прямой с. По признаку ||-ти прямой и плоскости прямая а1 || β и прямая а2 || β.
Слайд 40
По признаку ||-ти прямой и плоскости прямая а1
|| β и прямая а2 || β. Поэтому прямые
а1 и а2 не пересекают прямую с (она лежит в пл. β).
Слайд 41
Таким образом, в плоскости α через точку А
проходят две прямые а1 и а2, которые || прямой
с. Но это невозможно по аксиоме параллельных прямых:
через точку, не лежащую на данной прямой, можно провести на плоскости не более одной, параллельной данной.
Сл-но, наше предположение неверно, и плоскости α и β параллельны.
Слайд 42
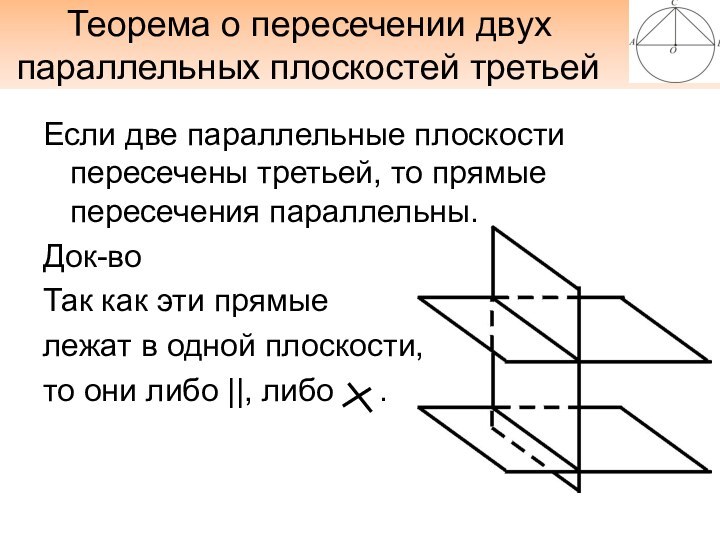
Теорема о пересечении двух
параллельных
плоскостей третьей
Если две параллельные плоскости пересечены третьей, то
прямые пересечения параллельны.
Док-во
Так как эти прямые
лежат в одной плоскости,
то они либо ||, либо .
Слайд 43
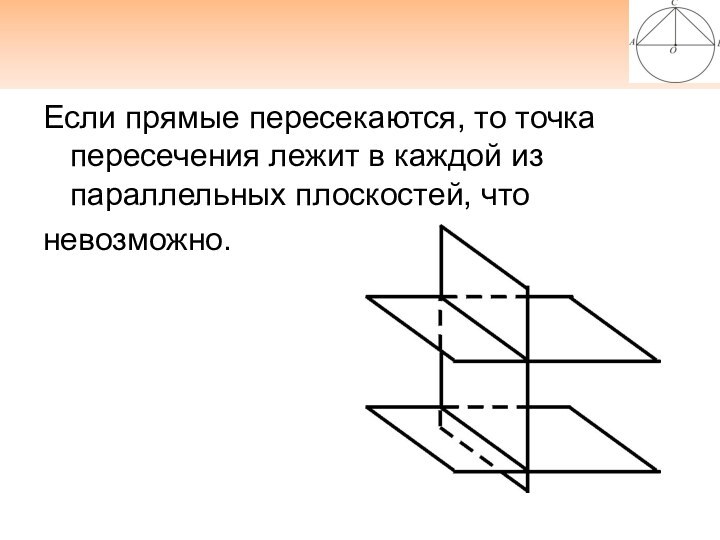
Если прямые пересекаются, то точка пересечения лежит в
каждой из параллельных плоскостей, что
невозможно.
Слайд 44
Теорема о равенстве
отрезков парал. прямых
Отрезки параллельных прямых, заключенные
между двумя параллельными плоскостями, равны.
Доказательство
Пусть α и β –
параллельные плоскости,
а и b – пересекающие их параллельные прямые; точки А1, А2, В1, В2 – точки пересечения прямых с плоскостями.
Надо доказать, что А1А2 = В1В2.
Слайд 45
Теорема
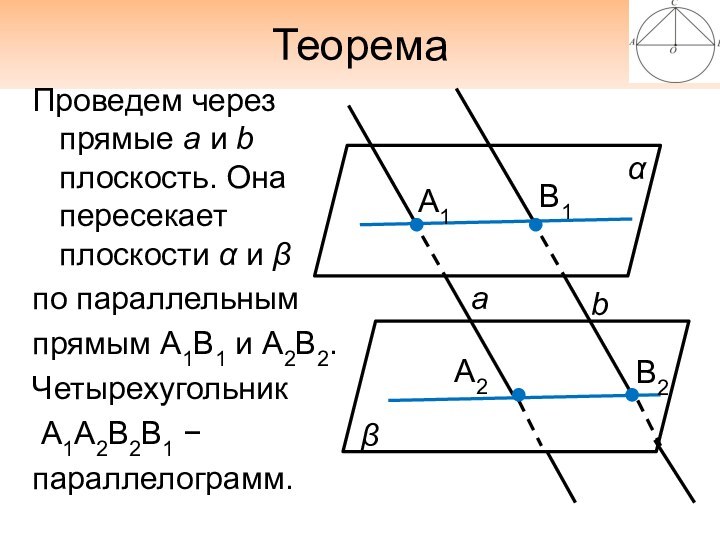
Проведем через прямые а и b плоскость. Она
пересекает плоскости α и β
по параллельным
прямым А1В1 и А2В2.
Четырехугольник
А1А2В2В1
параллелограмм.
Слайд 46
Литература
Геометрия, 7 – 11. Под ред. Погорелова
Домашнее задание
Выучите
определения и формулировки приведенных теорем наизусть
Подготовьтесь к диктанту
по этим формулировкам