- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Первообразная и интеграл
Содержание
- 2. Определение первообразной. Функция F называется первообразной для
- 4. Справедлива
- 5. Геометрический смысл первообразнойОсновному свойству первообразной можно придать
- 6. Таблица первообразных
- 7. Правила вычисления первообразныхПравило 1 Если F есть
- 8. Правило 2. Если F есть
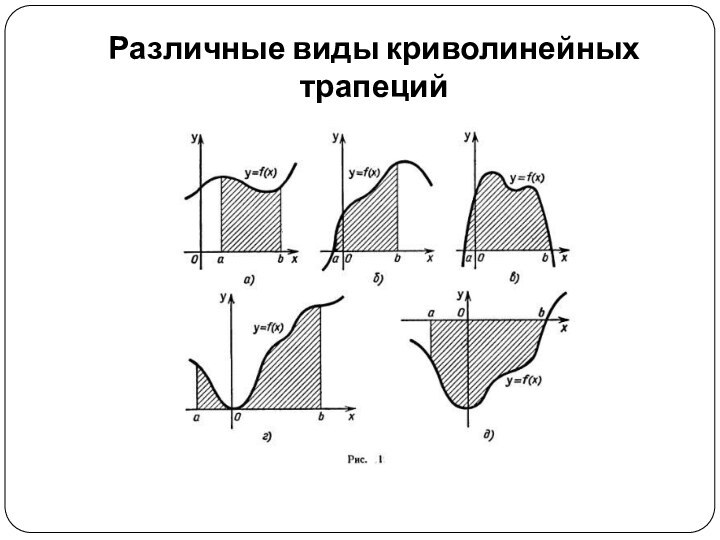
- 9. Криволинейная трапецияПусть на отрезке [а; b] оси
- 10. Различные виды криволинейных трапеций
- 11. Для вычисления площадей криволинейных трапеций применяют следующую
- 12. Интеграл. Формула Ньютона-Лейбница.Рассмотрим другой подход к
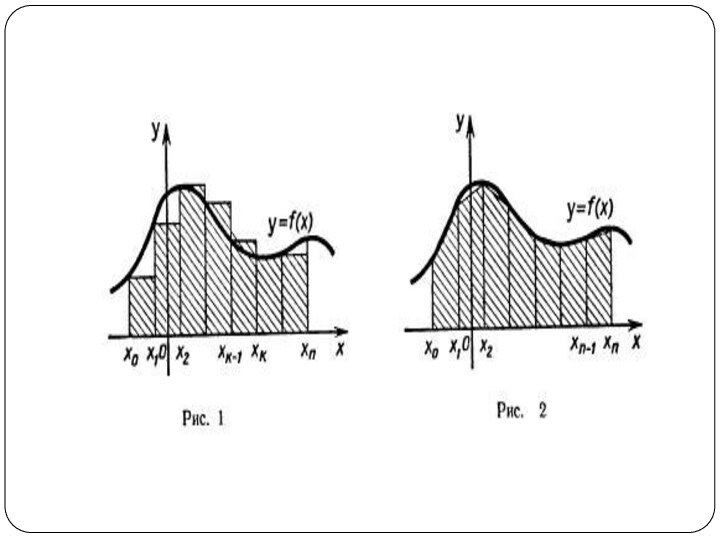
- 14. Разобьем отрезок [а; b] на n отрезков одинаковой длины точками x0 = а
- 15. а сумма площадей всех таких
- 16. Поэтому
- 17. Это
- 18. Итак, если f(х)≥0 на отрезке [а; b] то площадь S соответствующей криволинейной трапеции выражается формулой
- 19. Скачать презентацию
- 20. Похожие презентации
Определение первообразной. Функция F называется первообразной для функции f на заданном промежутке, если для всех х из этого промежутка







![Первообразная и интеграл Криволинейная трапецияПусть на отрезке [а; b] оси Ох задана непрерывная функция f,](/img/tmb/13/1277162/266227a08d6cf22886f5fa1bfcf4e63d-720x.jpg)


![Первообразная и интеграл Разобьем отрезок [а; b] на n отрезков одинаковой длины точками x0 = а](/img/tmb/13/1277162/b901134980efa9f035e3a40fbe5180f0-720x.jpg)



![Первообразная и интеграл Итак, если f(х)≥0 на отрезке [а; b] то площадь S соответствующей криволинейной трапеции выражается формулой](/img/tmb/13/1277162/84b4659369abb22a42c8d42baf040d88-720x.jpg)

Слайд 3
Основное свойство первообразной
Задача интегрирования состоит в том, чтобы
для заданной функции найти все ее первообразные. При решении
этой задачи важную роль играет следующее утверждение: Признак постоянства функции.Если F'(х) = 0 на некотором промежутке I,
то функция F — постоянная на этом промежутке. Все первообразные функции f можно записать с помощью одной формулы, которую называют общим видом первообразных для функции f.
Слайд 4
Справедлива следующая
теорема (основное свойство первообразных):
Теорема. Любая первообразная для функции
f на промежутке I может быть записана в виде F(x)+C,
где F (х) — одна из первообразных для функ-ции f (x) на промежутке I,
С — произвольная постоянная.
Слайд 5
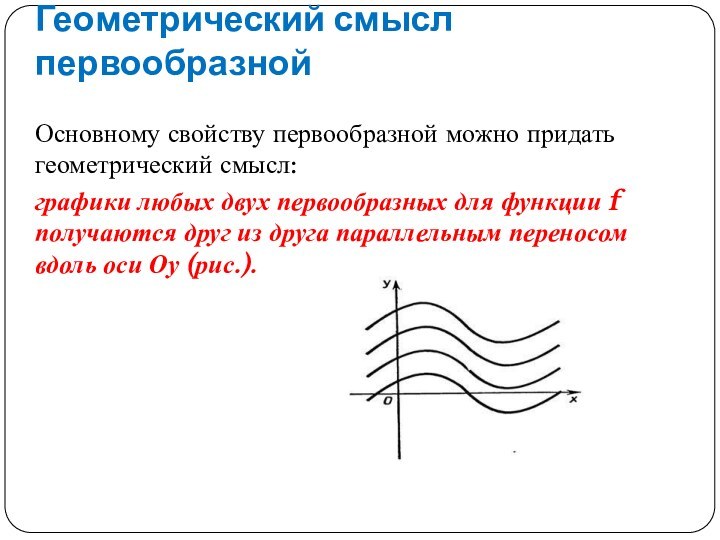
Геометрический смысл первообразной
Основному свойству первообразной можно придать геометрический
смысл:
графики любых двух первообразных для функции f получаются друг
из друга параллельным переносом вдоль оси Оу (рис.).
Слайд 7
Правила вычисления первообразных
Правило 1 Если F есть первообразная
для f, a G — первообразная для g, то
F+G есть первообразная для f+g.(F+G)'=F'+G'=f+g
Слайд 8
Правило 2. Если F есть первообразная
для f, a k — постоянная, то функция kF
— первообразная для kf. (kF)'=kF'=kf.Правило 3. Если F (х) есть первообразная для f (x), a k и b — постоянные, причем k≠0, то есть первообразная для f
(kx+b).
Слайд 9
Криволинейная трапеция
Пусть на отрезке [а; b] оси Ох
задана непрерывная функция f, не меняющая на нем знака.
Фигуру, ограниченную графиком этой функции, отрезком [а; b] и прямыми х = а и х = b (рис. 1), называют криволинейной трапецией.
Слайд 11
Для вычисления площадей криволинейных трапеций применяют следующую теорему:
Теорема.
Если f — непрерывная и неотрицательная на отрезке [а;
b] функция, a F — ее первообразная на этом отрезке, то площадь S соответствующей криволинейной трапеции) равна приращению первообразной на отрезке[а; b] т. е.
S=F(b)-F(a).
Слайд 12
Интеграл. Формула Ньютона-Лейбница.
Рассмотрим другой подход к задаче
вычисления площади криволинейной трапеции. Для простоты будем считать функцию
f неотрицательной и непрерывной на отрезке [а; b] тогда площадь S соответствующей криволинейной трапеции можно приближенно подсчитать следующим образом.
Слайд 15
а сумма площадей всех таких прямоугольников
(рис. 1) равна:
В силу непрерывности функции f объединение построенных
прямоугольников при большом n, т. е. при малом Δx, «почти совпадает» с интересующей нас криволинейной трапецией.
Слайд 16
Поэтому возникает
предположение, что Sn≈S при больших n. (Коротко говорят: «Sn
стремится к S при n, стремящемся к бесконечности»— и пишут: Sn→S при n→∞.) Предположение это правильно. Более того, для любой непрерывной на отрезке [а; b] функции а (не обязательно неотрицательной) Sn при n→∞ стремится к некоторому числу.
Слайд 17
Это число
называют (по пределению) интегралом функции f от а до b и
обозначают , т.е.при n→∞ (1 ) (читается: «Интеграл от а до b эф от икс дэ икс»). Числа а и b называются пределами интегрирования: а — нижним пределом, b — верхним. Знак называют знаком интеграла.
Функция f называется подынтегральной функцией, а переменная х — переменной интегрирования.





























