Слайд 2
Прямой поиск
Идея алгоритма:
Совмещаем начало строки и подстроки.
Выполняем проверку: совпадают ли все буквы подстроки с соответствующими
буквами строки.
Если совпали не все буквы – сдвигаем подстроку на одну позицию вправо, снова выполняем проверку и т.д.
Поиск прекращаем, когда найдем подстроку или строка закончится.
Слайд 3
Прямой поиск
Обозначения:
St – строка, Sl – подстрока
m –
длина строки, n – длина подстроки
First – номер символа
строки, с которым совмещаем первый символ подстроки
Логика процедуры:
First:=1;
repeat
t:=check(first); {количество совпавших символов}
if t<>n then {если совпали не все символы}
inc(first);{сдвигаем подстроку}
until (n=t) or (first>m-n+1);
if t=n then writeln('YES!!!! , позиция ',first) else writeln('NO...');
Слайд 4
функцию Check
В функцию передается один параметр – номер
символа строки, с которым совмещаем первый символ подстроки. Проверку
начинаем с начала подстроки и движемся вправо, пока буквы строки и подстроки совпадают. Движение прекращаем, когда встретим нарушение или подстрока закончится.
function check(k:byte):byte;
var i:integer;
begin
i:=0;
while (i check:=i;
end;
Слайд 5
Алгоритм Бойера и Мура
Задача 1. Модификация прямого поиска.
В прямом поиске проверка на совпадение начинается с начала
подстроки и продвижение по строке происходит вправо.
Измените программу так, чтобы проверка начиналась с конца подстроки.
Введите переменную Last – номер символа строки, с которым совмещаем последний символ подстроки .
Слайд 6
Задача 2.
Для введенной с клавиатуры строки составить
таблицу: для каждого символа записать число, равное расстоянию от
конца строки до этого символа. В таблице должно быть 255 чисел (по количеству всех возможных символов).
Если символа в строке нет – в таблицу записать число, равное длине строки.
Если символ встречается в строке несколько раз – в таблицу записать расстояние от конца строки до ближайшего к концу строки такого символа (последнего такого символа)
Слайд 7
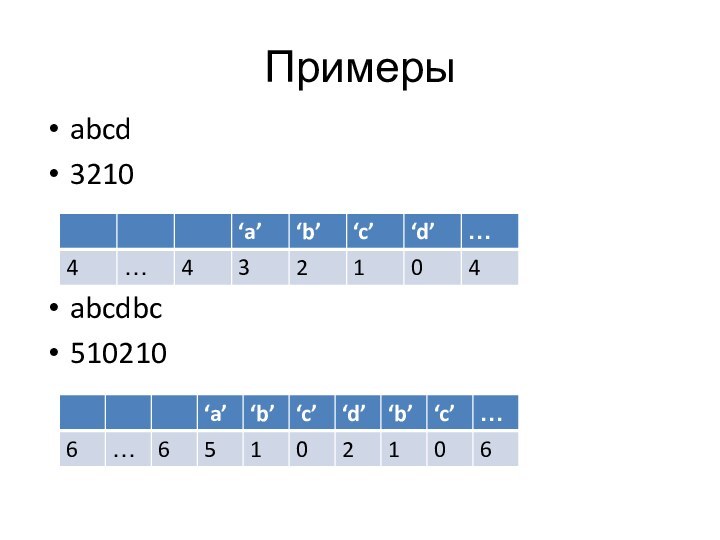
Примеры
abcd
3210
abcdbc
510210
Слайд 8
Для хранения таблицы используем массив А
Var a :
array[char] of byte;
Вопросы:
Что будет храниться в массиве?
Как нумеруются
элементы?
Работу с массивом a
Если написать оператор a[‘d’]:=5, то ...
Если введена строка St=’fghj’, тогда оператор a[st[3]]:=1 выделит из строки третий символ (‘h’), и в ячейку, соответствующую этому символу, будет записано число ...
Слайд 9
Логика решения задачи
Заполним весь массив числом N -
длиной строки
Пойдем по строке слева направо, и для каждой
буквы строки в таблицу будем записывать расстояние от этой буквы до конца строки (если i – номер буквы, тогда (n-i) – расстояние от этой буквы до конца строки)
Слайд 10
Если буква встречается в строке несколько раз, то
в таблицу будет записано расстояние до последней такой буквы.
Например, возьмем строку ‘МАМАША’ и рассмотрим процесс заполнения массива А
Слайд 11
В заполненной таблице всегда будет один ноль: в
ячейке, соответствующей последней букве (в нашем случае a[‘А’]=0).
При
заполнении таблицы возьмем цикл от 1 до (n-1).
Тогда для последней буквы будет получен не ноль, а расстояние до ближайшей к концу строки такой буквы. (в нашем случае a[‘A’]=2 - расстояние до ближайшей к концу буквы ‘А’ равно двум).
Слайд 12
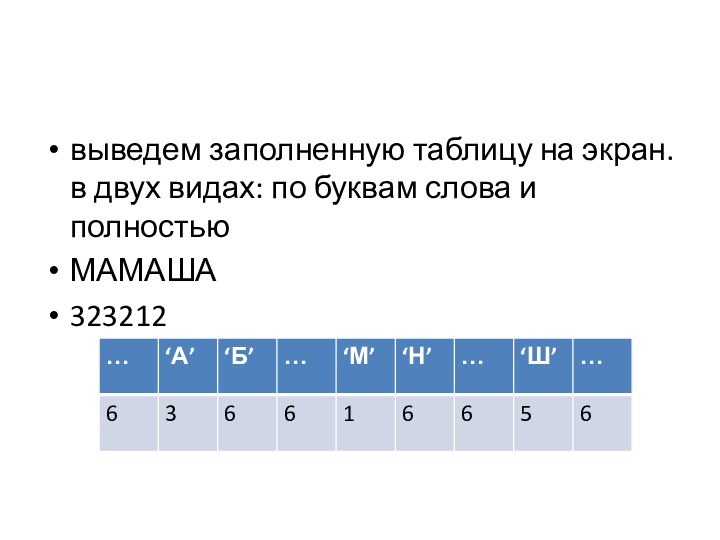
выведем заполненную таблицу на экран. в двух видах:
по буквам слова и полностью
МАМАША
323212
Слайд 13
Идея алгоритма Бойера и Мура
Совмещаем начало строки и
подстроки. Проверку на совпадение начинаем с конца подстроки (Задача
1).
В случае несовпадения будем сдвигать подстроку вправо, причем постараемся выполнить сдвиг не на одну позицию, как в прямом поиске, а на несколько позиций.
Пример
МАШЕТ МАШЕ МАМАША
МАМАША
Слайд 14
Сравниваем последнюю букву подстроки (‘А’) и соответствующую букву
строки (пробел).
Пробела в подстроке нет, поэтому подстроку можно
сдвинуть на всю длину.
МАШЕТ МАШЕ МАМАША
МАМАША
Слайд 15
Сравниваем последнюю букву подстроки (‘А’) и соответствующую букву
строки (‘М’).
Буква ‘М’ есть в подстроке, расстояние от
конца подстроки до этой буквы равно трем, поэтому подстроку сдвинем на три позиции. То есть «пододвинем» букву ‘М’ подстроки под букву ‘М’ строки.
МАШЕТ МАШЕ МАМАША
МАМАША
Слайд 16
После сдвига оказалось, что последняя буква подстроки совпадает
с соответствующей буквой строки.
Это частичное совпадение (подстрока частично
совпадает со строкой). Поэтому нужно снова выполнить сдвиг. Так как расстояние до ближайшей к концу строки буквы ‘А’ равно двум, сдвинем на 2 позиции.
МАШЕТ МАШЕ МАМАША
МАМАША
Полное совпадение, поиск прекращаем.
Нашли подстроку в строке, выполнив 3 сдвига подстроки. В прямом поиске нужно выполнить 11 сдвигов.
Слайд 17
Задание
Выполнить трассировку алгоритма на примере
МАШЕТСЯ МАМАШКИНА МАШКА
МАШКА
Слайд 18
Описание алгоритма
Пусть last – номер буквы строки, которой
соответствует последняя буква подстроки. Тогда st[last] – эта буква,
а a[st[last]] – расстояние до такой же буквы в подстроке. Сдвигая подстроку на величину a[st[last]], мы добьемся совмещения букв. Если буквы st[last] нет в подстроке, то для нее величина a[st[last]] равна длине подстроки, то есть будет осуществлен сдвиг на всю длину подстроки.
Слайд 19
Описание алгоритма
После выхода из цикла необходимо определить, входит
ли подстрока в строку, и если входит, определить позицию.
Так как переменная last указывает на символ строки, которому соответствует последний символ подстроки, то номер (last-n+1) соответствует первому символу подстроки.
Слайд 20
Общая логика алгоритма
last:=N;
repeat
t:=check(last);
if tn then
last:=last+a[st[last]]
until
(n=t) or (last>m);
if t=n then writeln('YES!!!! ',last-n+1)
else writeln('NO...');
Слайд 21
Задание
Ппридумать пример подстроки и строки, для которых алгоритм
Бойера и Мура неэффективен (работает так же, как прямой
поиск)
Слайд 22
Усложненный вариант алгоритма Бойера и Мура
Этот вариант отличается
величиной сдвига в случае частичного совпадения.
Пример
PMDCBAAHFES
CMKABA
В упрощенном варианте
– сдвиг подстроки на 2 позиции (совмещаем буквы ‘A’).
PMDCBAA
CMKABA
Назовем этот сдвиг сдвигом №1 (сдвиг под последнюю букву)
Слайд 23
Подстрока со строкой совпадает частично.
Это значит, что
в процессе сравнения при движении справа налево после нескольких
совпадающих букв нам встретились различные (‘C’ и ’A’).
Символ строки, в котором произошло нарушение (буква ‘C’), будем называть стоп-символом.
Совместим стоп-символ с таким же символом подстроки. Для нашего примера нужно выполнить сдвиг подстроки на 3 позиции
PMDCBAA
CMKABA
Назовем этот сдвиг сдвигом №2 (сдвиг под стоп-символ)
В данном случае сдвиг № 2 больше.
Слайд 24
Как определить величину сдвига №2 в программе?
Символ строки,
соответствующий последнему символу подстроки, имеет номер last.
Если t
– количество совпавших символов подстроки и строки, то стоп-символ имеет номер last-t.
В таблице ему соответствует число a[st[last-t]]. Если выполнить сдвиг на эту величину, то нужная буква «уйдет» не под стоп-символ, а под символ с номером last.
PMDCBAA
CMKABA
Поэтому сдвинуть нужно на a[st[last-t]]-t.
Слайд 25
В усложненном варианте будем выполнять сдвиг подстроки на
максимальную величину, то есть максимальный из двух сдвигов.
if
t<>n then
last:=last+max(a[st[last]],a[st[last-t]]-t);
Если нет частичного совпадения (t=0), то сдвиг №2 будет равен сдвигу№1.
Сдвиг №2 может быть отрицательным, когда a[st[last-t]]
Слайд 26
Задание
Придумать примеры подстроки и строки, такие, чтобы при
поиске возникала ситуация частичного совпадения, и
сдвиг №2 был отрицательным
сдвиг
№2 был положительным, но был бы меньше, чем сдвиг №1
сдвиг №2 был положительным, и был бы больше, чем сдвиг №1
Слайд 27
Алгоритм Кнута, Мориса и Пратта
Обозначениея.
Для строки St
- L(st) – это максимальная длина начала строки, совпадающего
с концом строки.
Пример:
ST L(St)
aba 1
abcab 2
a 0
ab 0
ababa 3
Слайд 28
Подготовительная задача
Ввести строку. Вычислить L для каждого начала
этой строки.
Пример.
Пусть St=‘abcababc’.
Тогда нужно вычислить L
для
a, ab, abc, abca, abcab, abcaba, abcabab, abcababc.
Запишем значения L в массив
abcababc
00012123
Заполнять массив будем последовательно, начиная со второго элемента (a[1] считаем равным нулю).
Слайд 29
Для вычисления A[i] воспользуемся следующим.
На предыдущем шаге
вычислено A[i-1], то есть для предыдущего начала строки St
известно L – количество первых символов, совпадающих с последними.
Слайд 30
Сравниваем L+1-й символ и i-ый.
Если они равны,
тогда получаем, что L+1 первых символов совпадают с L+1
последними, то есть можно записать, что A[i] равно L+1.
Если L+1-й и i-ый символы не совпадают, тогда нам нужно найти другое начало, совпадающее с концом (не максимальное), и посмотреть, какая буква идет после него.
Длину меньшего начала, совпадающего с концом, найдем по формуле L=A[L].
Слайд 31
Опять сравниваем i-ую и L+1-ую букву.
Если они
совпадают, тогда в a[i] запишем L+1.
Если они не
совпадают – тогда L снова присвоим значение А[L] и так далее до тех пор, пока не найдем совпадение или не получим L, равное нулю.
Слайд 32
Вычисление A[i]
len:=a[i-1];
while (sl[i]sl[len+1]) and (len>0) do len:=a[len];
{из цикла
выйдем, когда len=0 или (len+1)-ая буква совпала с i-ой}
if
sl[len+1]=sl[i] then a[i]:=len+1
else a[i]:=0;
Слайд 33
Задания
Для строки abcababc выполните вручную заполнение массива А
для всех i.
Придумайте пример строки, для которой при вычислении
какого-либо a[i] тело цикла while выполняетcя 3 раза
Придумайте строку, для которой в массиве А будет получено A[i]
1 для какого-либо i. Например, a[i-1]=6, a[i]=2.
Придумайте пример строки, для которой A[i] будет больше, чем [i/2], для какого-либо i.
Слайд 34
Упрощенный вариант алгоритма Кнута, Мориса и Пратта
Пусть у
нас есть строка St и подстрока Sl. Склеим подстроку
и строку, поставив между ними разделитель – символ, которого нет в подстроке и строке.
подстрока строка
Слайд 35
Для получившейся строки St2 будем заполнять массив А.
Если на каком-то шаге получим, что A[i]=N (длине подстроки),
то это значит, что подстрока найдена (первые N символов совпали с последними N символами
Слайд 36
Общая логика процедуры
St2:=sl+'#'+st;
a[1]:=0;
i:=1;
repeat
inc(i);
Вычислить A[i]
until (a[i]=n)
or (i=n+m+1);
if a[i]=n then writeln('YES!!! ')
else writeln('NO...');






![Поиск подстроки в строке Для хранения таблицы используем массив АVar a : array[char] of byte;Вопросы: Что](/img/tmb/14/1327250/44129f213cdd3c26b8c8afe4a848614a-720x.jpg)










![Поиск подстроки в строке Общая логика алгоритмаlast:=N;repeat t:=check(last); if tn then last:=last+a[st[last]]until (n=t) or (last>m);if t=n](/img/tmb/14/1327250/c8c9189f819e193224a3c1e1b78278b6-720x.jpg)








![Поиск подстроки в строке Для вычисления A[i] воспользуемся следующим. На предыдущем шаге вычислено A[i-1], то есть](/img/tmb/14/1327250/71d689082024446bbee63dd2674aa265-720x.jpg)

![Поиск подстроки в строке Опять сравниваем i-ую и L+1-ую букву. Если они совпадают, тогда в a[i]](/img/tmb/14/1327250/e614dd2491226222ac5d38bc2627ce21-720x.jpg)
![Поиск подстроки в строке Вычисление A[i]len:=a[i-1];while (sl[i]sl[len+1]) and (len>0) do len:=a[len];{из цикла выйдем, когда len=0 или](/img/tmb/14/1327250/ac048c681f4e8b3de585b895a697d035-720x.jpg)



![Поиск подстроки в строке Общая логика процедуры St2:=sl+'#'+st; a[1]:=0; i:=1; repeat inc(i); Вычислить A[i]](/img/tmb/14/1327250/e0bcf622bd4e5b53edf10f77c950e8b4-720x.jpg)