Слайд 2
Последовательность решения задач на построение линии пересечения кривых
поверхностей
1) выясняем вид и расположение заданных поверхностей относительно друг
друга (врезка или проницание) и плоскостей проекций
(задана ли проецирующая поверхность);
2) определяем характер линии пересечения: замкнутая кривая одна, или несколько;
3) определяем опорные точки (экстремальные и очерковые);
4) определяем промежуточные точки;
5) соединяем найденные точки плавной кривой. Определяем видимость проекций линии пересечения и очерков поверхностей, обводим чертеж.
Слайд 3
Построение линии пересечения кривых поверхностей из условия принадлежности
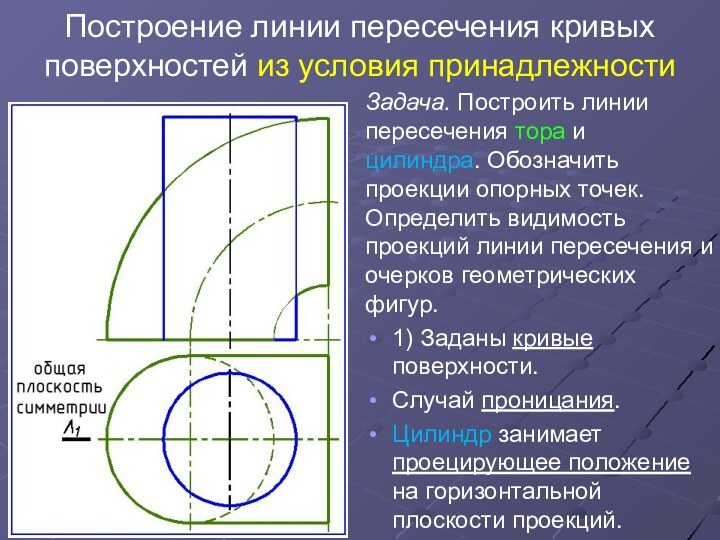
Задача. Построить линии пересечения тора и цилиндра. Обозначить проекции
опорных точек. Определить видимость проекций линии пересечения и очерков геометрических фигур.
1) Заданы кривые поверхности.
Случай проницания.
Цилиндр занимает проецирующее положение на горизонтальной плоскости проекций.
Слайд 4
Построение линии пересечения кривых поверхностей из условия принадлежности
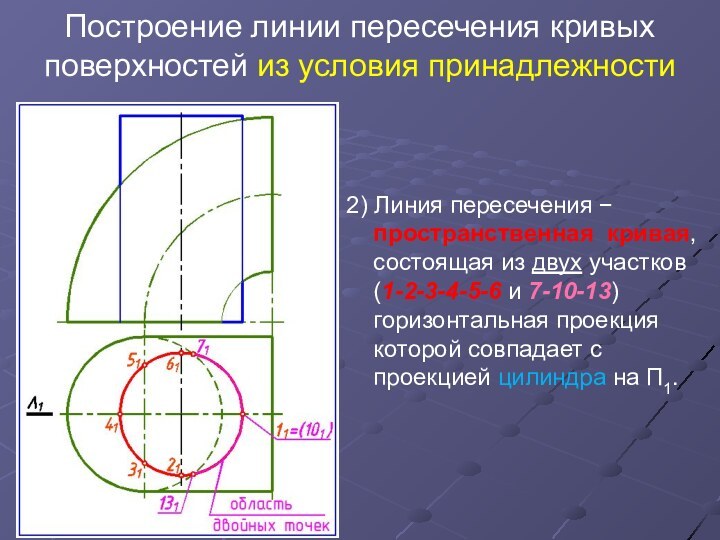
2) Линия пересечения пространственная кривая, состоящая из двух
участков (1-2-3-4-5-6 и 7-10-13) горизонтальная проекция которой совпадает с проекцией цилиндра на П1.
Слайд 5
Построение линии пересечения кривых поверхностей из условия принадлежности
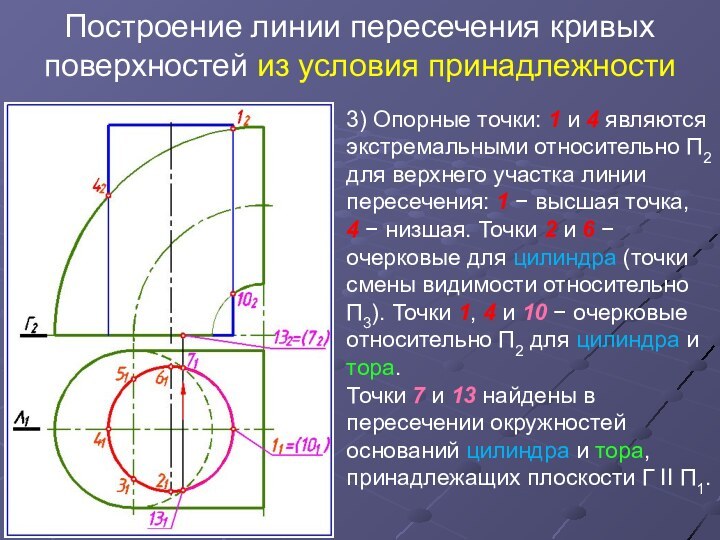
3) Опорные точки: 1 и 4 являются экстремальными относительно
П2 для верхнего участка линии пересечения: 1 высшая точка,
4 низшая. Точки 2 и 6 очерковые для цилиндра (точки смены видимости относительно П3). Точки 1, 4 и 10 очерковые относительно П2 для цилиндра и тора.
Точки 7 и 13 найдены в пересечении окружностей оснований цилиндра и тора, принадлежащих плоскости Г II П1.
Слайд 6
Построение линии пересечения кривых поверхностей из условия принадлежности
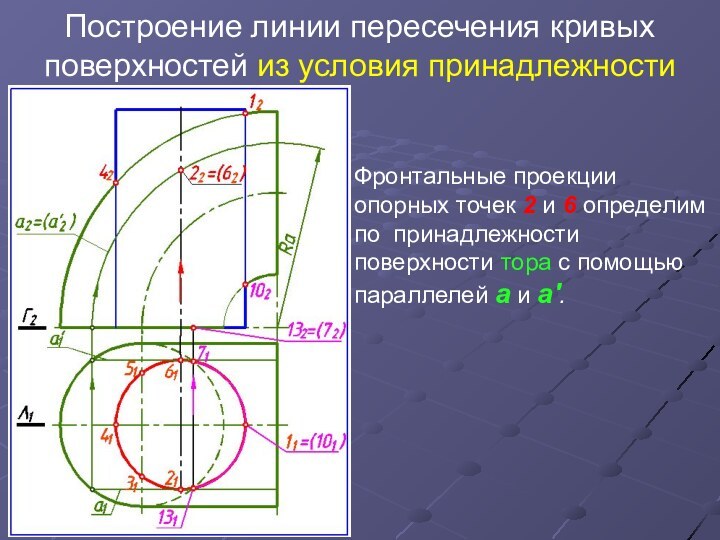
Фронтальные проекции опорных точек 2 и 6 определим по
принадлежности поверхности тора с помощью параллелей а и а'.
Слайд 7
Построение линии пересечения кривых поверхностей из условия принадлежности
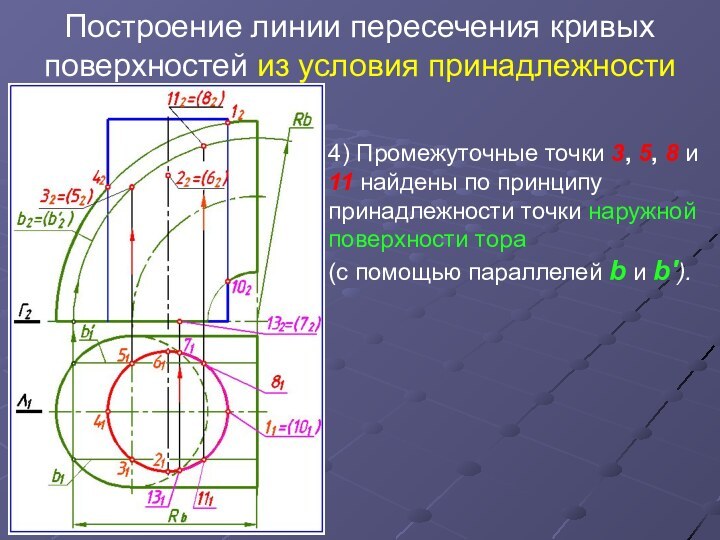
4) Промежуточные точки 3, 5, 8 и 11 найдены
по принципу принадлежности точки наружной поверхности тора
(с помощью параллелей b и b').
Слайд 8
Построение линии пересечения кривых поверхностей из условия принадлежности
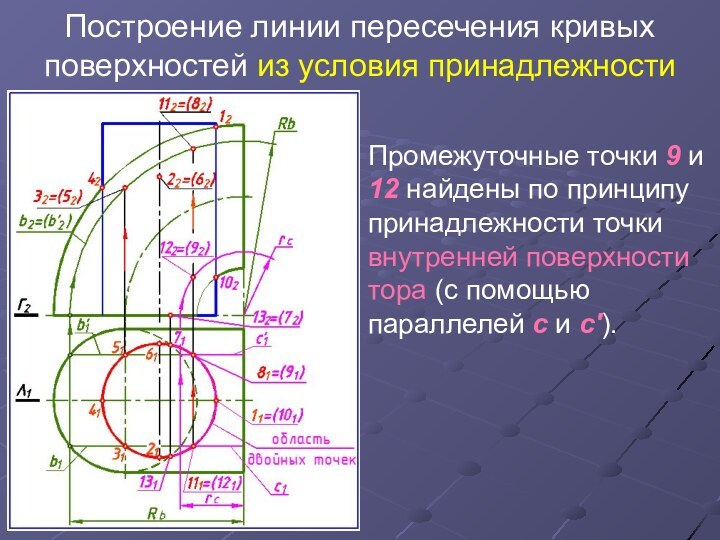
Промежуточные точки 9 и 12 найдены по принципу принадлежности
точки внутренней поверхности тора (с помощью параллелей с и с').
Слайд 9
Построение линии пересечения кривых поверхностей из условия принадлежности
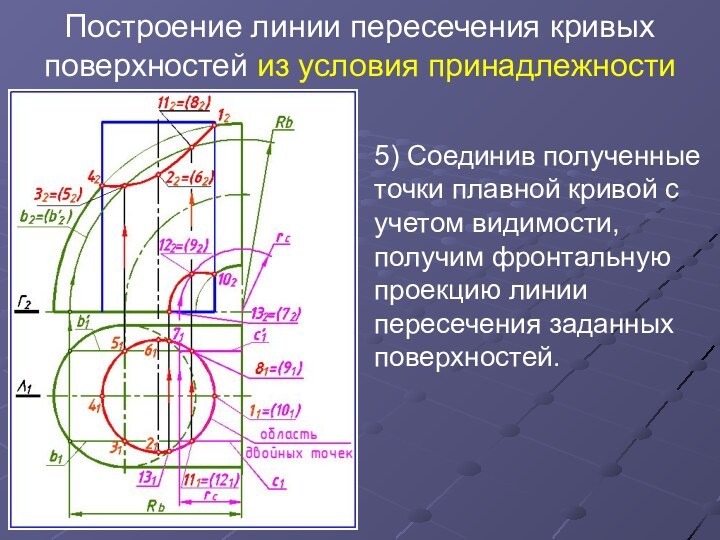
5) Соединив полученные точки плавной кривой с учетом видимости,
получим фронтальную проекцию линии пересечения заданных поверхностей.
Слайд 10
Построение линии пересечения кривых поверхностей из условия принадлежности
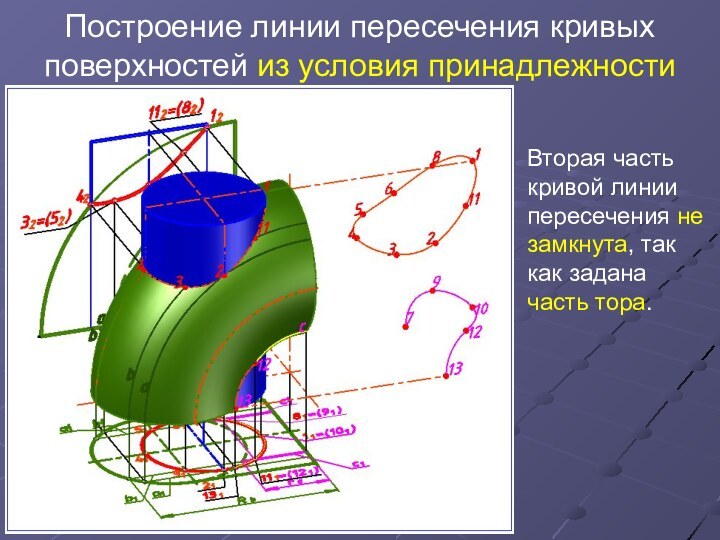
Вторая часть кривой линии пересечения не замкнута, так как
задана часть тора.
Слайд 11
Построение линии пересечения кривых поверхностей из условия принадлежности
Задача. Построить линии пересечения конуса и цилиндра. Обозначить проекции
опорных точек. Определить видимость проекций линии пересечения и очерков геометрических фигур.
1) Заданы кривые поверхности (конус и половина цилиндра). Случай проницания. Цилиндр занимает проецирующее положение относительно П2.
Слайд 12
Построение линии пересечения кривых поверхностей из условия принадлежности
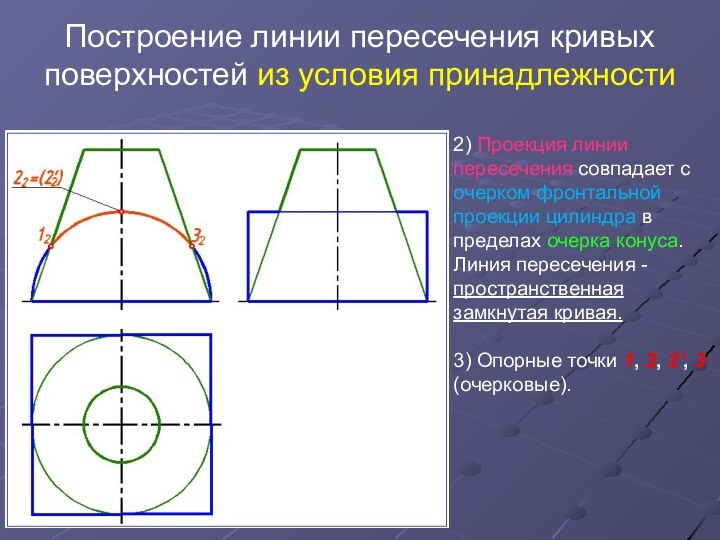
2)
Проекция линии пересечения совпадает с очерком фронтальной проекции цилиндра
в пределах очерка конуса. Линия пересечения - пространственная замкнутая кривая.
3) Опорные точки 1, 2, 2', 3 (очерковые).
Слайд 13
Построение линии пересечения кривых поверхностей из условия принадлежности
3)
Опорные точки 1, 2, 2', 3 (очерковые) определены из
условия принадлежности поверхности конуса
(очерк – ось).
Слайд 14
Построение линии пересечения кривых поверхностей из условия принадлежности
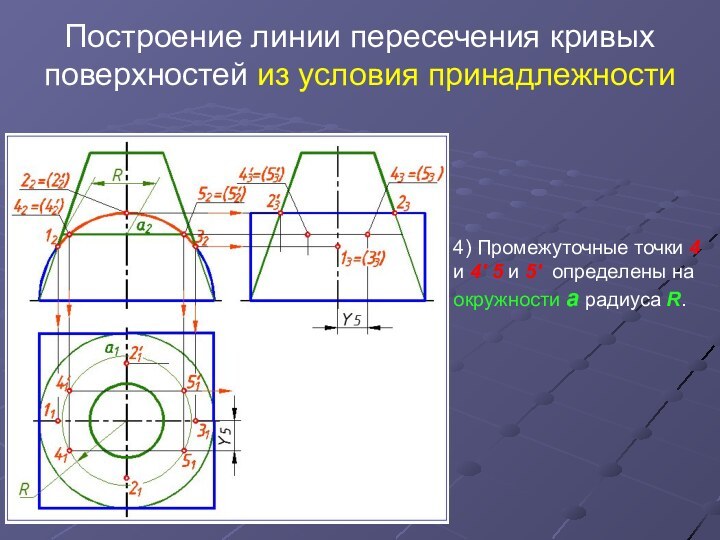
4)
Промежуточные точки 4 и 4' 5 и 5' определены
на окружности а радиуса R.
Слайд 15
Построение линии пересечения кривых поверхностей из условия принадлежности
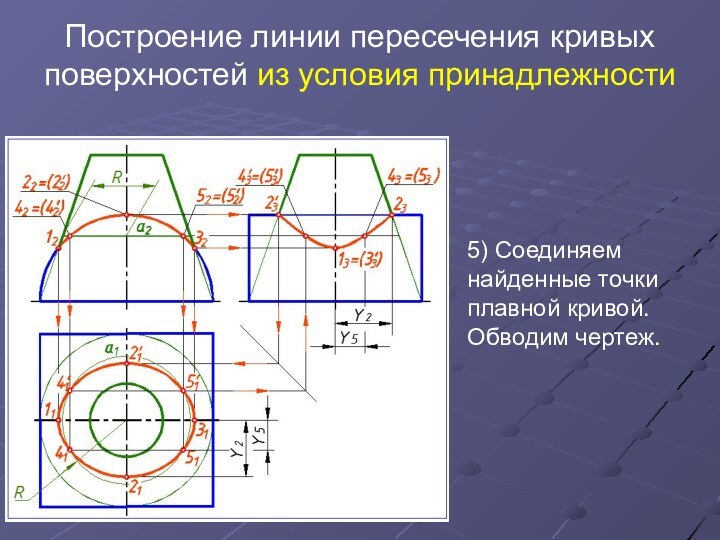
5)
Соединяем найденные точки плавной кривой. Обводим чертеж.
Слайд 16
Построение линии пересечения кривых поверхностей из условия принадлежности
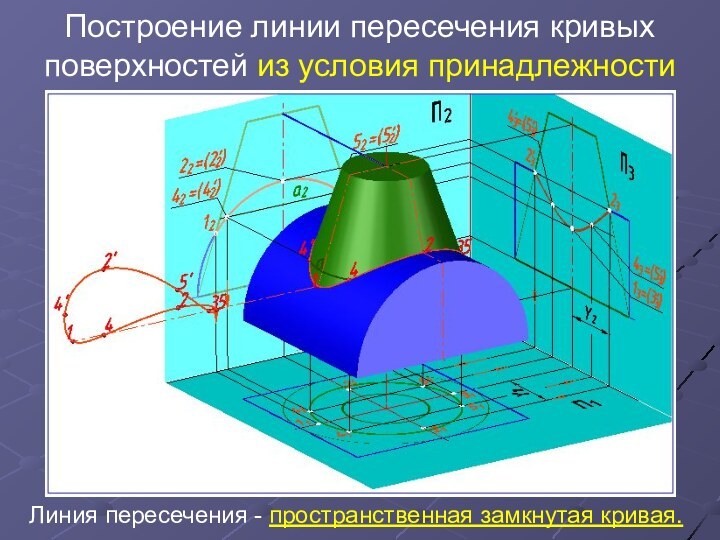
Линия пересечения - пространственная замкнутая кривая.
Слайд 17
Построение линии пересечения кривых поверхностей способом секущих плоскостей
Задача.
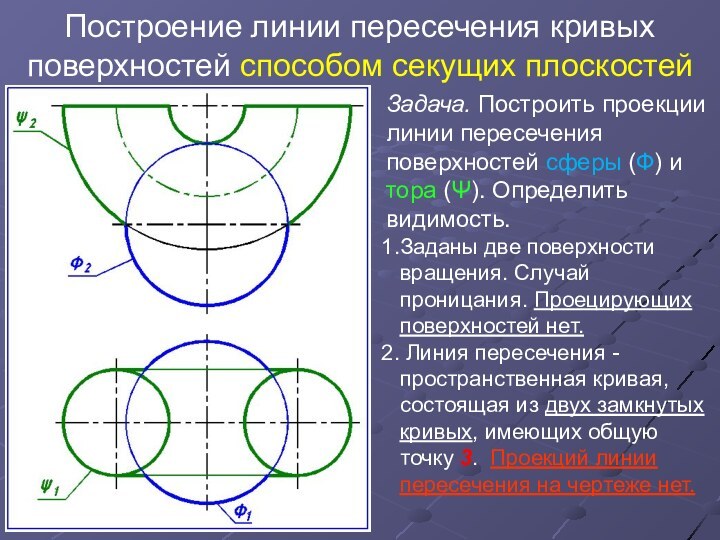
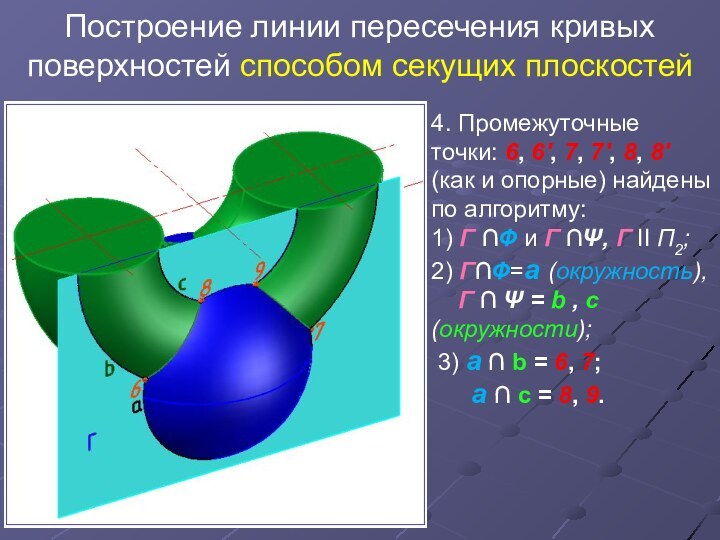
Построить проекции линии пересечения поверхностей сферы (Ф) и тора
(Ψ). Определить видимость.
Заданы две поверхности вращения. Случай проницания. Проецирующих поверхностей нет.
Линия пересечения - пространственная кривая, состоящая из двух замкнутых кривых, имеющих общую точку 3. Проекций линии пересечения на чертеже нет.
Слайд 18
Построение линии пересечения кривых поверхностей способом секущих плоскостей
3.
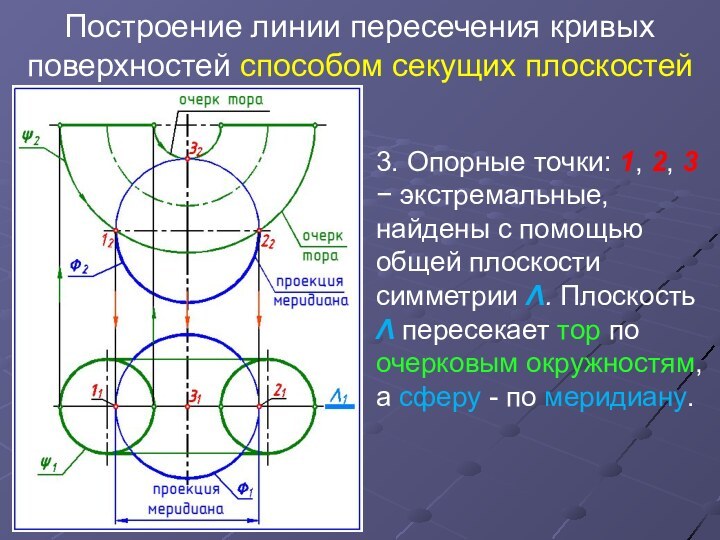
Опорные точки: 1, 2, 3 экстремальные, найдены с
помощью общей плоскости симметрии Λ. Плоскость Λ пересекает тор по очерковым окружностям, а сферу - по меридиану.
Слайд 19
Построение линии пересечения кривых поверхностей способом секущих плоскостей
3.
Опорные точки: 1, 2, 3 экстремальные, найдены с
помощью общей плоскости симметрии Λ. Плоскость Λ пересекает тор по очерковым окружностям, а сферу - по меридиану.
Слайд 20
Построение линии пересечения кривых поверхностей способом секущих плоскостей
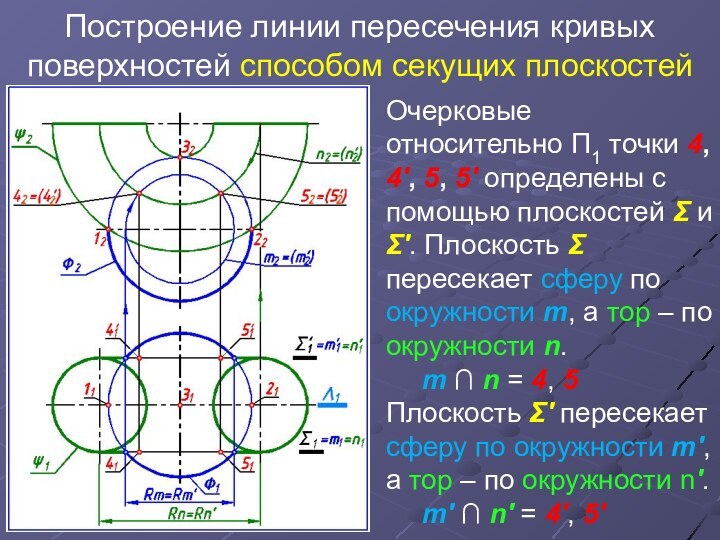
Очерковые
относительно П1 точки 4, 4', 5, 5' определены с
помощью плоскостей Σ и Σ'. Плоскость Σ пересекает сферу по окружности m, а тор – по окружности n.
m ∩ n = 4, 5
Плоскость Σ' пересекает сферу по окружности m', а тор – по окружности n'.
m' ∩ n′ = 4', 5'
Слайд 21
Построение линии пересечения кривых поверхностей способом секущих плоскостей
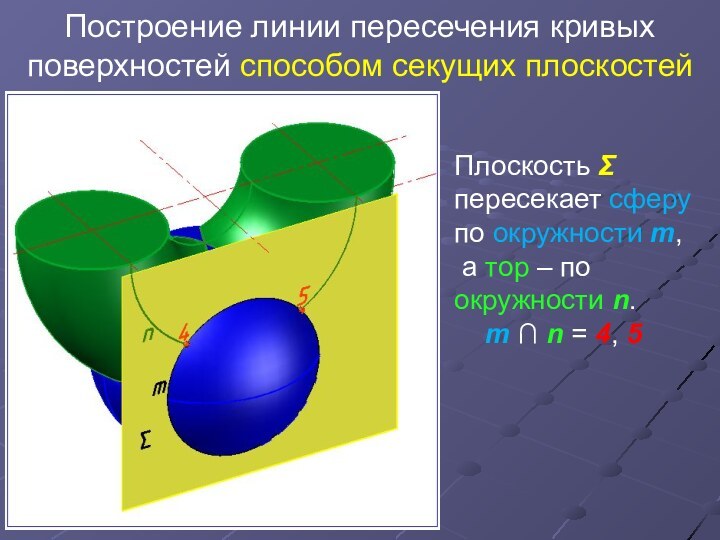
Плоскость
Σ пересекает сферу по окружности m,
а тор –
по окружности n.
m ∩ n = 4, 5
Слайд 22
Построение линии пересечения кривых поверхностей способом секущих плоскостей
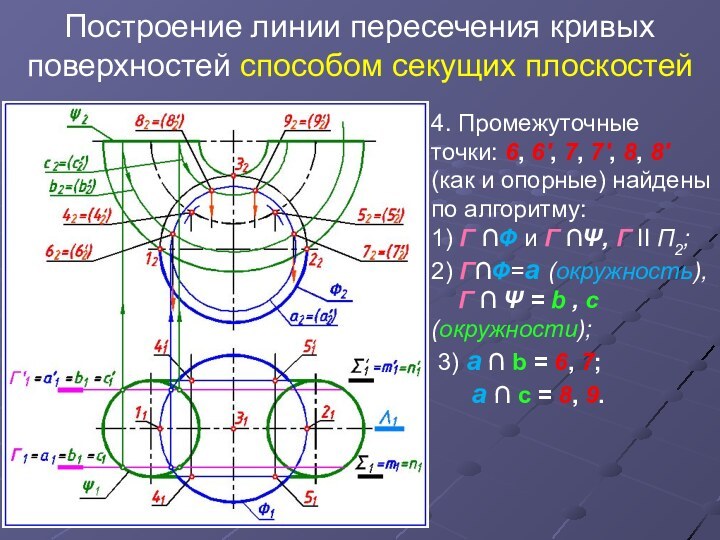
4.
Промежуточные точки: 6, 6', 7, 7', 8, 8' (как
и опорные) найдены по алгоритму:
1) Г ∩Ф и Г ∩Ψ, Г II П2;
2) Г∩Ф=а (окружность),
Г ∩ Ψ = b , с (окружности);
3) а ∩ b = 6, 7;
а ∩ с = 8, 9.
Слайд 23
Построение линии пересечения кривых поверхностей способом секущих плоскостей
4.
Промежуточные точки: 6, 6', 7, 7', 8, 8' (как
и опорные) найдены по алгоритму:
1) Г ∩Ф и Г ∩Ψ, Г II П2;
2) Г∩Ф=а (окружность),
Г ∩ Ψ = b , с (окружности);
3) а ∩ b = 6, 7;
а ∩ с = 8, 9.
Слайд 24
Построение линии пересечения кривых поверхностей способом секущих плоскостей
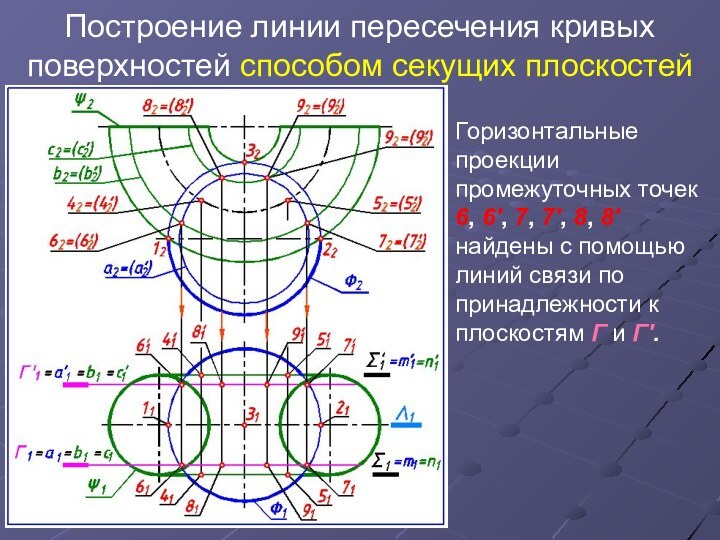
Горизонтальные
проекции промежуточных точек 6, 6', 7, 7', 8, 8'
найдены с помощью линий связи по принадлежности к плоскостям Г и Г'.
Слайд 25
Построение линии пересечения кривых поверхностей способом секущих плоскостей
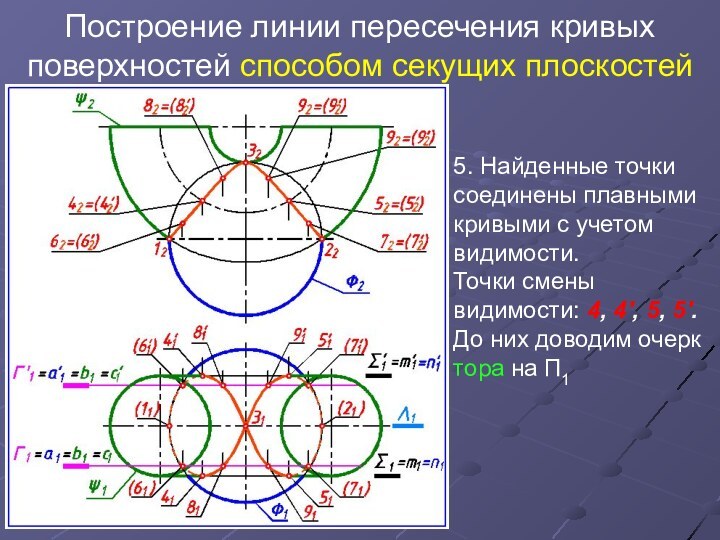
5.
Найденные точки соединены плавными кривыми с учетом видимости.
Точки смены
видимости: 4, 4', 5, 5'.
До них доводим очерк тора на П1
Слайд 26
Построение линии пересечения кривых поверхностей способом секущих плоскостей
Слайд 27
Построение линии пересечения кривых поверхностей способом секущих плоскостей
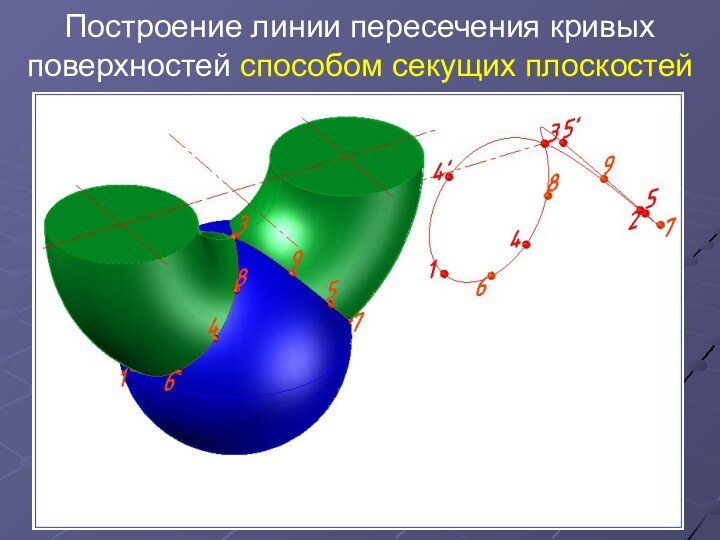
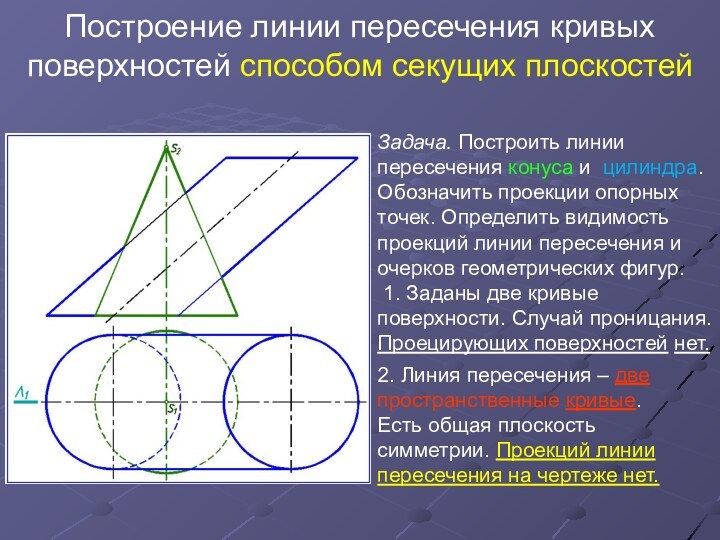
Задача.
Построить линии пересечения конуса и цилиндра. Обозначить проекции опорных
точек. Определить видимость проекций линии пересечения и очерков геометрических фигур.
1. Заданы две кривые поверхности. Случай проницания. Проецирующих поверхностей нет.
2. Линия пересечения – две пространственные кривые.
Есть общая плоскость симметрии. Проекций линии пересечения на чертеже нет.
Слайд 28
Построение линии пересечения кривых поверхностей способом секущих плоскостей
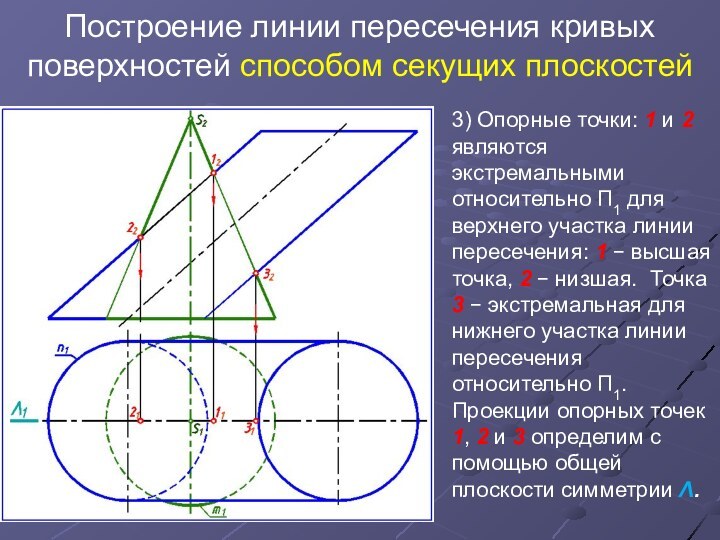
3)
Опорные точки: 1 и 2 являются экстремальными относительно П1
для верхнего участка линии пересечения: 1 высшая точка, 2 низшая. Точка 3 экстремальная для нижнего участка линии пересечения относительно П1.
Проекции опорных точек 1, 2 и 3 определим с помощью общей плоскости симметрии Λ.
Слайд 29
Построение линии пересечения кривых поверхностей способом секущих плоскостей
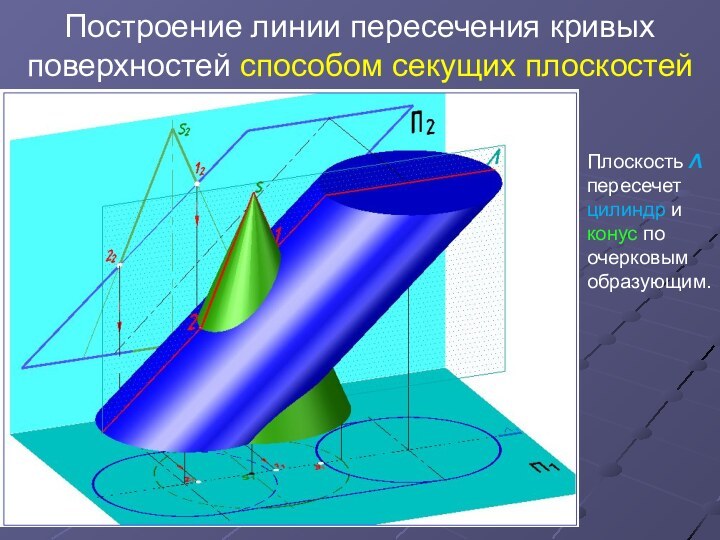
Плоскость
Λ пересечет цилиндр и конус по очерковым образующим.
Слайд 30
Построение линии пересечения кривых поверхностей способом секущих плоскостей
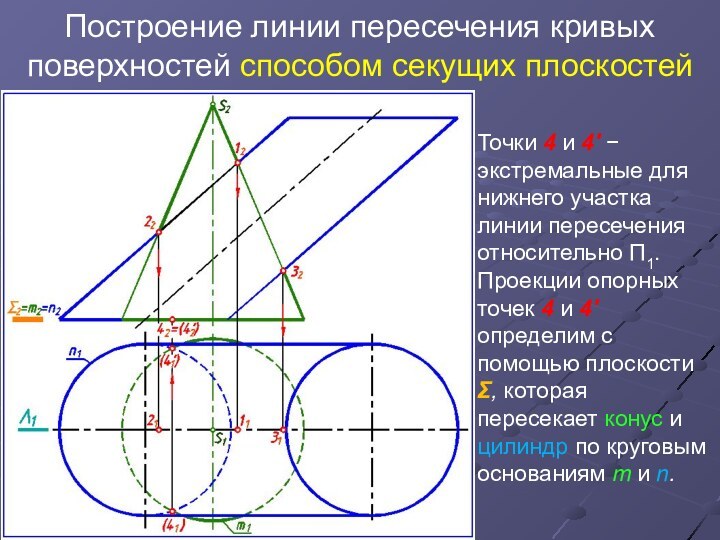
Точки
4 и 4′ экстремальные для нижнего участка линии
пересечения относительно П1.
Проекции опорных точек 4 и 4' определим с помощью плоскости Σ, которая пересекает конус и цилиндр по круговым основаниям m и n.
Слайд 31
Построение линии пересечения кривых поверхностей способом секущих плоскостей
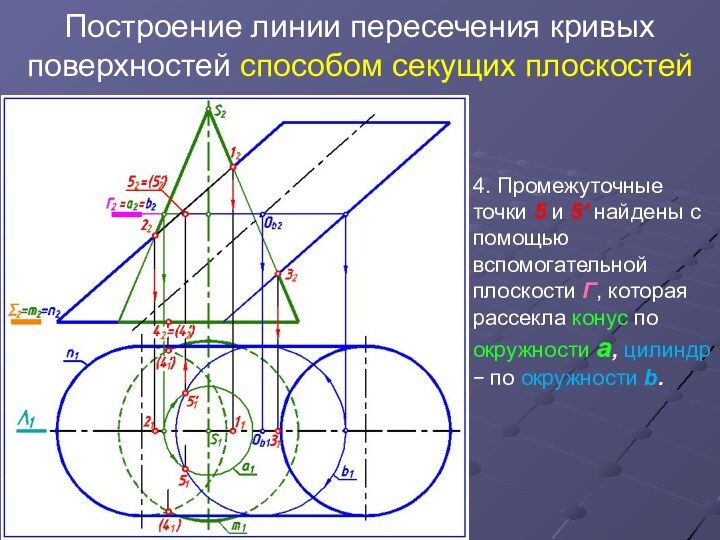
4.
Промежуточные точки 5 и 5' найдены с помощью вспомогательной
плоскости Г, которая рассекла конус по окружности а, цилиндр по окружности b.
Слайд 32
Построение линии пересечения кривых поверхностей способом секущих плоскостей
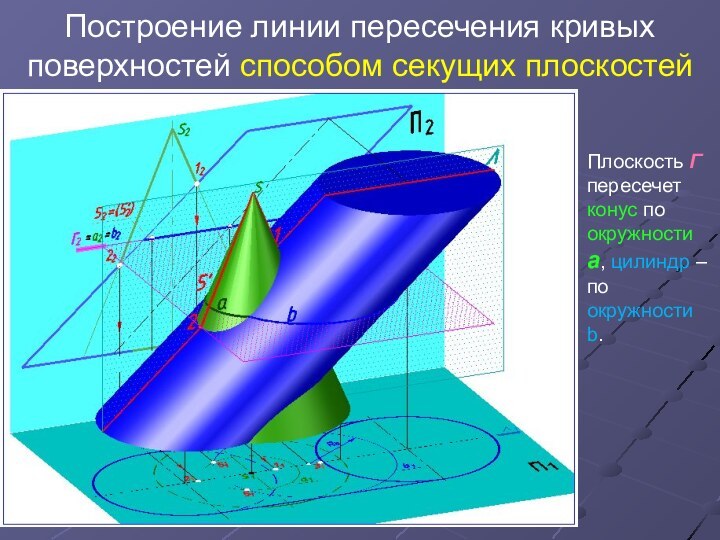
Плоскость
Г пересечет конус по окружности а, цилиндр – по
окружности b.
Слайд 33
Построение линии пересечения кривых поверхностей способом секущих плоскостей
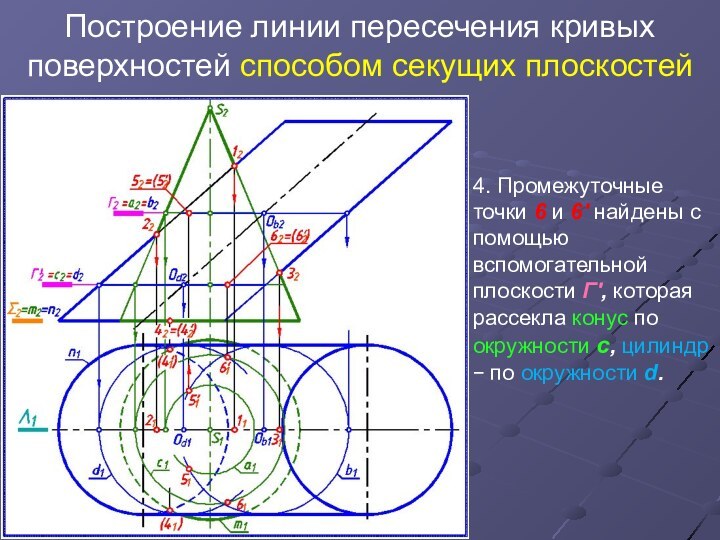
4.
Промежуточные точки 6 и 6' найдены с помощью вспомогательной
плоскости Г′, которая рассекла конус по окружности с, цилиндр по окружности d.
Слайд 34
Построение линии пересечения кривых поверхностей способом секущих плоскостей
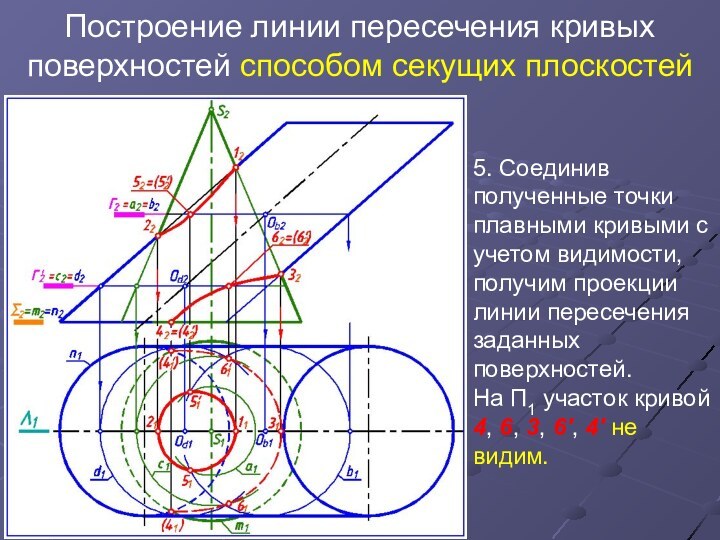
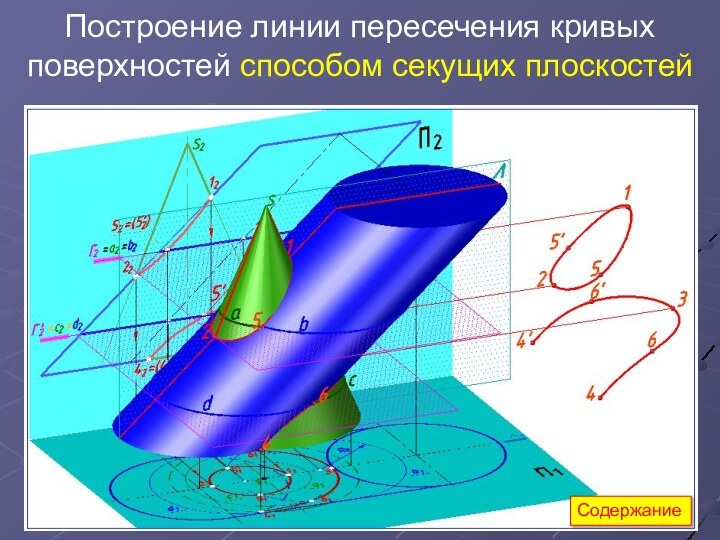
5.
Соединив полученные точки плавными кривыми с учетом видимости, получим
проекции линии пересечения заданных поверхностей.
На П1 участок кривой 4, 6, 3, 6', 4' не видим.