Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Построение треугольника по трем элементам.

Содержание

2. Цель урока: рассмотреть задачи на
3. Чертёжные инструменты
4. напоминание. Задача 1 : на
5. Задача 2: отложить от данного
6. Затем проведем окружность того же радиуса
7. DСПостроение треугольника по двум сторонам и углу
8. DСПостроение треугольника по стороне и двум прилежащим
9. СПостроим луч а.Отложим отрезок АВ, равный P1Q1.Построим
10. Итог урока.
11. №286 Постройте треугольник по стороне,
14. Домашнее задание.
15. Скачать презентацию
16. Похожие презентации

Цель урока: рассмотреть задачи на построение треугольника по трем элементам; совершенствовать навыки решения задач на построение.

Главная
Разное
Построение треугольника по трем элементам.

Цель урока: рассмотреть задачи на построение треугольника по трем элементам;

напоминание. Задача 1 : на данном луче от его начала

Задача 2: отложить от данного луча угол, равный данному.

Затем проведем окружность того же радиуса с центром в начале данного

DСПостроение треугольника по двум сторонам и углу между ними. Угол hkhПостроим луч

DСПостроение треугольника по стороне и двум прилежащим к ней углам. Угол h1k1h2Построим

СПостроим луч а.Отложим отрезок АВ, равный P1Q1.Построим дугу с центром в т.

Итог урока. Рассмотрим схему, по которой

№286 Постройте треугольник по стороне, прилежащему к ней углу и

Слайды презентации

Слайд 2 Цель урока:
рассмотреть задачи на

Цель урока: рассмотреть задачи на построение треугольника по трем

построение треугольника по трем элементам;
совершенствовать навыки решения

задач на построение.

Слайд 3 Чертёжные инструменты

Слайд 4 напоминание.
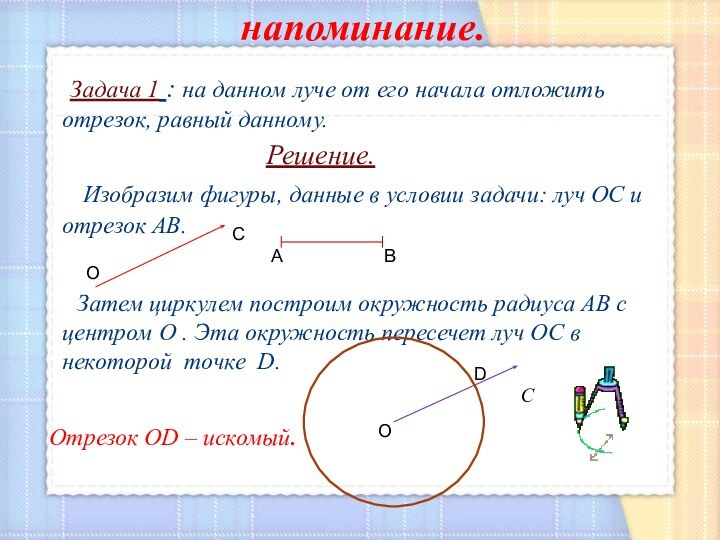
Задача 1 : на данном

луче от его начала отложить отрезок, равный данному.

Решение.
Изобразим фигуры, данные в условии задачи: луч ОС и отрезок АВ.

Затем циркулем построим окружность радиуса АВ с центром О . Эта окружность пересечет луч ОС в некоторой точке D.
С
Отрезок OD – искомый.

Слайд 5 Задача 2: отложить от данного луча

угол, равный данному.

Решение.
Изобразим фигуры, данные в условии: угол с вершиной А и луч ОМ.

Проведем окружность произвольного радиуса с центром в вершине А данного угла. Эта окружность пересекает стороны угла в точках В и С.

Слайд 6 Затем проведем окружность того же радиуса с

Затем проведем окружность того же радиуса с центром в начале

центром в начале данного луча ОМ. Она пересекает луч

в точке D. После этого построим окружность с центром D, радиус, которой равен ВС. Окружности пересекаются в
двух точках. Одну обозначим
буквой Е. Получим угол МОЕ

Слайд 7 D
С
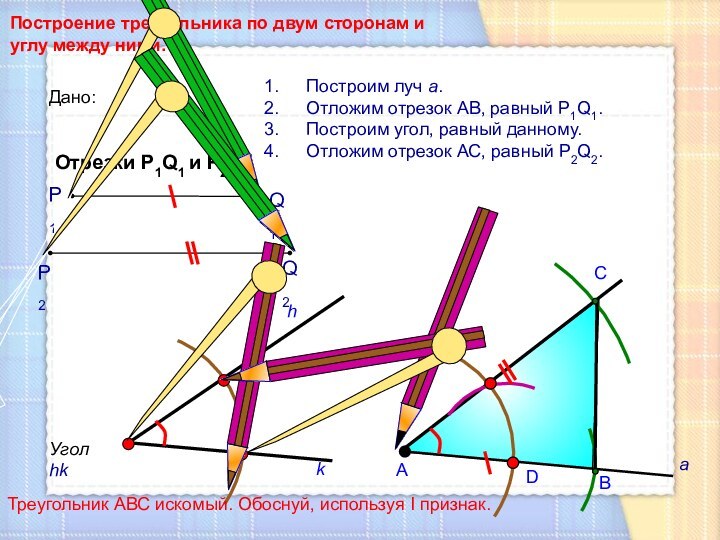
Построение треугольника по двум сторонам и углу между

DСПостроение треугольника по двум сторонам и углу между ними. Угол hkhПостроим

ними.
Угол hk
h
Построим луч а.
Отложим отрезок АВ, равный P1Q1.
Построим

угол, равный данному.
Отложим отрезок АС, равный P2Q2.

Треугольник АВС искомый. Обоснуй, используя I признак.

Дано:

Отрезки Р1Q1 и Р2Q2

Слайд 8 D
С
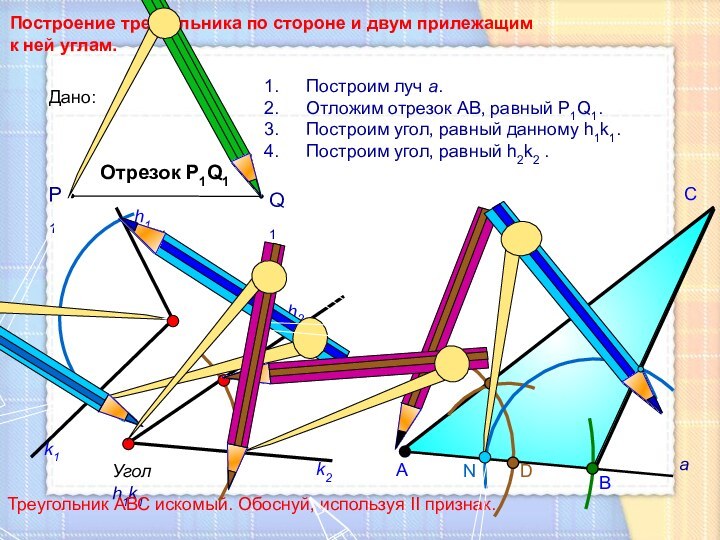
Построение треугольника по стороне и двум прилежащим к

DСПостроение треугольника по стороне и двум прилежащим к ней углам. Угол

ней углам.
Угол h1k1
h2
Построим луч а.
Отложим отрезок АВ, равный

P1Q1.
Построим угол, равный данному h1k1.
Построим угол, равный h2k2 .

Треугольник АВС искомый. Обоснуй, используя II признак.

Дано:

Отрезок Р1Q1

Слайд 9 С
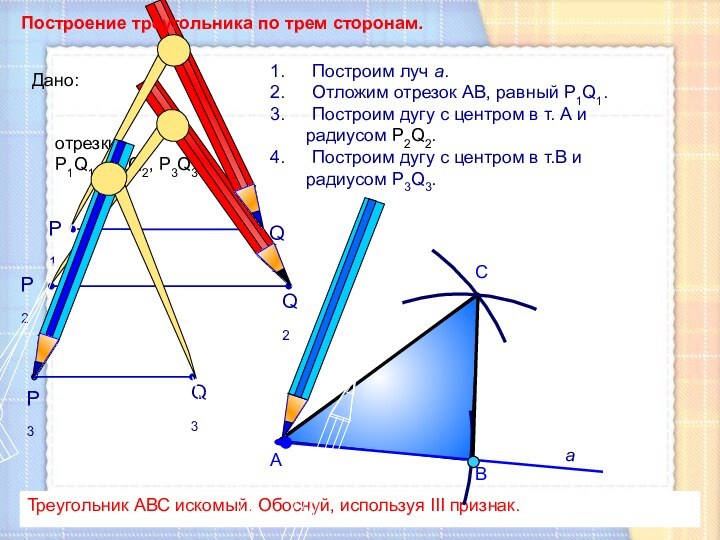
Построим луч а.
Отложим отрезок АВ, равный P1Q1.
Построим дугу

СПостроим луч а.Отложим отрезок АВ, равный P1Q1.Построим дугу с центром в

с центром в т. А и

радиусом Р2Q2.
Построим дугу с центром в т.В и
радиусом P3Q3.

Треугольник АВС искомый. Обоснуй, используя III признак.

Дано:

отрезки
Р1Q1, Р2Q2, P3Q3.

Построение треугольника по трем сторонам.

Слайд 10 Итог урока.

Итог урока. Рассмотрим схему, по которой обычно решают

Рассмотрим схему, по которой обычно решают задачи на построение

с помощью циркуля и линейки.
Она состоит из частей:
1. Отыскание способа решения задачи путём установления связей между искомыми элементами и данными задачи. Анализ дает возможность составить план решения задачи на построение.
2. Выполнение построения по намеченному плану.
3. Доказательство того, что построенная фигура удовлетворяет условиям задачи.
4. Исследование задачи, т.е. выяснение вопроса о том, при любых ли данных задача имеет решение, и если имеет, то сколько решений.

Слайд 11 №286
Постройте треугольник по стороне, прилежащему к

ней углу и биссектрисе треугольника, проведенной из вершины этого

угла.
Решение.
Требуется построить треугольник АВС, у которого одна из сторон, например АС, равна данному отрезку P1Q1, угол А равен данному
углу hк, а биссектриса АD этого треугольника равна данному
отрезку P2Q2.
Даны отрезки P1 Q1 и P2Q2 и угол hк (рисунок а).

P1 Q1 P2 Q2
h
рисунок а
к

Слайд 12

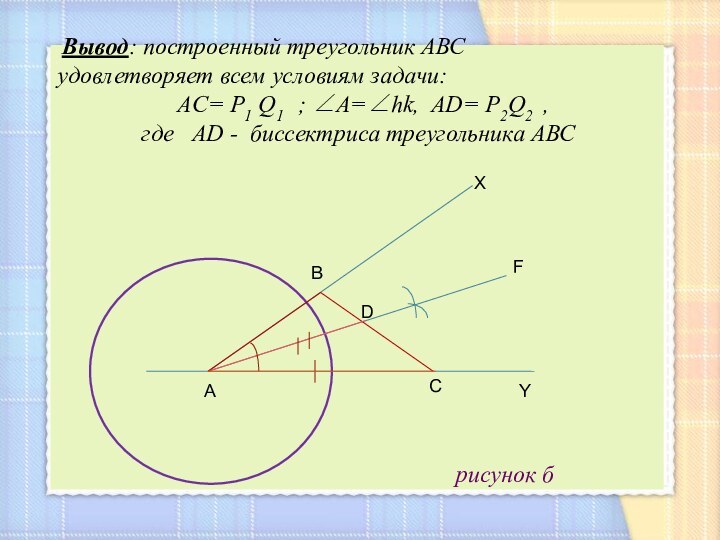
Построение (рисунок б).
1) Построим угол ХАУ, равный данному углу hк.
2)На луче АУ отложим отрезок АС, равный данному отрезку P1Q1.
3)Построим биссектрису АF угла ХАУ.
4) На луче АF отложим отрезок АD, равный данному отрезку Р2Q2
5) Искомая вершина В — точка пересечения луча АХ с прямой СD. Построенный треугольник АВС удовлетворяет всем условиям задачи: АС=Р1Q1,
А = hк, АD = Р2Q2 , где АD — биссектриса треугольника АВС.