Слайд 2
Тема лекции: Предпочтительные числа и ряды предпочтительных чисел
Изучаемые
вопросы:
1 Оптимизация объектов стандартизации
и параметрическая стандартизация
2 Предпочтительные
числа на основе
геометрической прогрессии
3 Предпочтительные числа на основе
арифметической прогрессии
4 Специальные ряды чисел
Слайд 3
Оптимизация объектов стандартизации и параметрическая стандартизация
Оптимизация объектов стандартизации
заключается в определении оптимальных параметров (главных),
а также значений
всех других показателей, обеспечивающих заданный уровень качества.
Цель оптимизации – достижение оптимальной степени упорядочения и максимально возможной эффективности по выбранному показателю, используя параметрическую стандартизацию.
Параметрическая стандартизация – деятельность, направленная на выбор и установление обоснованных числовых значений параметров, подчиняющихся определенной математической закономерности.
Слайд 4
Параметрическая стандартизация
Современное производство характеризуется широкой номенклатурой выпускаемых изделий.
Выпуск
чрезмерно большой номенклатуры изделий одинакового назначения и имеющих незначительные
конструктивные исполнения, затрудняет их унификацию, увеличивает сроки подготовки их производства, а также стоимость производства.
Стандарты на ряды основных параметров изделий являются основой для сокращения номенклатуры и числа типоразмеров производимых изделий.
Параметры изделий делятся на основные и главные.
Слайд 5
Основные и главные параметры
Основные параметры определяют характерные конструктивно-технологические
и эксплуатационные свойства изделий и процессов.
Главные параметры выбираются из
числа основных параметров.
Главные параметры наиболее полно характеризуют свойства изделий и процессов.
В зависимости от назначения и особенностей изделия или процесса может быть один или несколько главных параметров.
Параметрические ряды машин, приборов и других объектов стандартизации устанавливаются на базе предпочтительных чисел.
Слайд 6
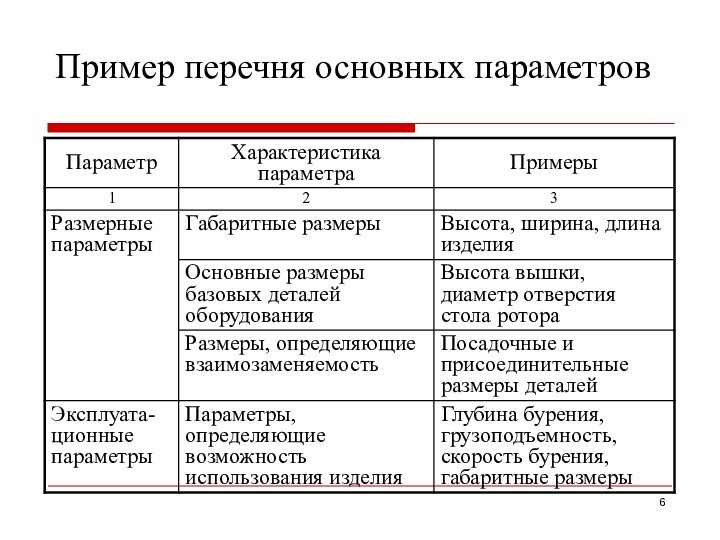
Пример перечня основных параметров
Слайд 7
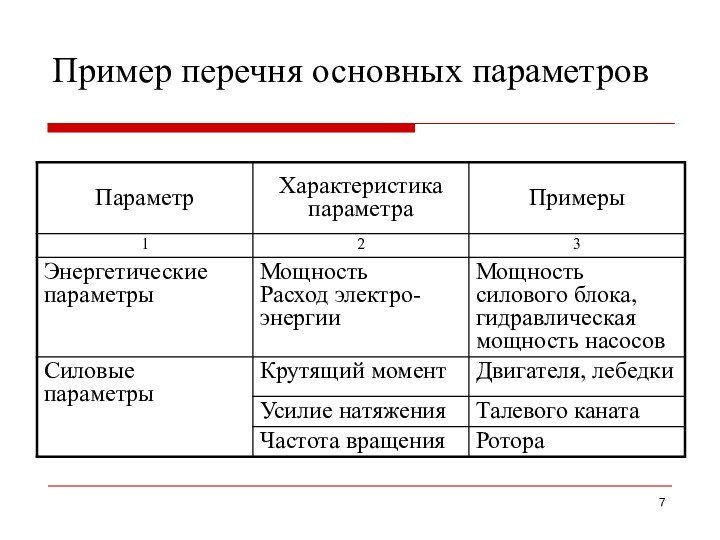
Пример перечня основных параметров
Слайд 8
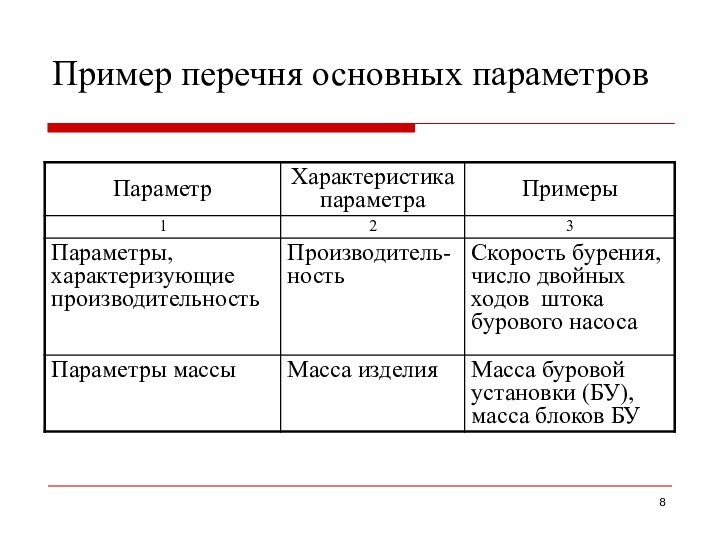
Пример перечня основных параметров
Слайд 9
Система предпочтительных чисел
⃞ Предпочтительные числа и ряды предпочтительных
чисел
являются основанием для выбора величин и градаций параметров всех
видов изделий.
⃞ Использование предпочтительных чисел позволяет уменьшить количество типоразмеров изделий, экономно использовать исходные материалы, согласовать и увязать между собой параметры изделия, полуфабрикатов, материалов, транспортных средств, технологического, контрольно-измерительного и другого оборудования (по мощности, габаритам, емкости и т.п.).
Слайд 10
Предпочтительные числа
В машиностроении и приборостроении предпочтительные числа, принятые
за основу при назначении точности, линейных размеров, углов, радиусов,
уступов, сокращают номенклатуру режущего и измерительного инструмента, штампов, пресс-форм, приспособлений. Это способствует росту уровня взаимозаменяемости, повышению серийности, технического уровня и качества продукции, расширению объемов ее производства, улучшению организации инструментального хозяйства на предприятии.
Слайд 11
Предпочтительные числа
⃞ Использование предпочтительных чисел при конструировании позволяет
обеспечить взаимозаменяемость деталей и сборочных единиц, унификацию конструкций машин.
⃞
Системы предпочтительных чисел установлены межгосударственным стандартом ГОСТ 8032-84
⃞ Виды предпочтительных чисел:
- на основе геометрической прогрессии;
- на основе арифметической прогрессии;
- специальные ряды чисел.
Слайд 12
Предпочтительные числа на основе геометрической прогрессии
⃞ Стандартом
установлены следующие ряды чисел:
- 4 основных (R5, R10,
R20, R40);
- 2 дополнительных (R80, R160).
⃞ В эти ряды входят предпочтительные числа,
представляющие собой округленные значения иррациональных чисел, составляющих геометрическую прогрессию со знаменателем
Q = , (1)
где R – показатель степени, равный 5; 10; 20; 40; 80 и 160.
Слайд 13
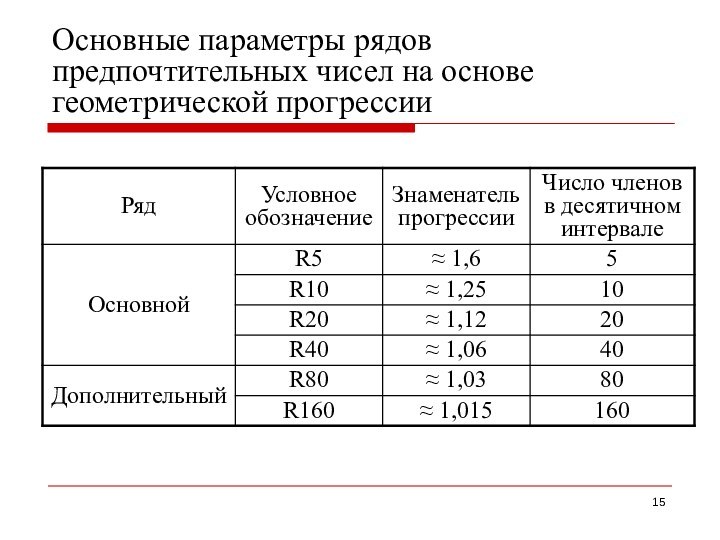
Основные параметры рядов предпочтительных чисел на основе геометрической
прогрессии
Знаменателями рядов геометрической прогрессии являются округленные числа. Например, точное
значение знаменателя ряда R5 равно 1,5849, округленное - ≈ 1,6.
Относительная разность между расчетными
и округленными числами значений знаменателей
ряда на основе геометрической прогрессии
находится в пределах от плюс 1,26 до минус 1,01 %.
⃞ Степень корня «R» входит в условное обозначение
рядов: пятый ряд – R5, десятый ряд – R10 и т.д.
Слайд 14
Предпочтительные числа на основе геометрической прогрессии
⃞ Выражение i-го
члена геометрической прогрессии в общем виде определяется из выражения:
gi
= ± 10 i/R , (2)
где i – целое число в интервале от 0 до R.
Отступления от предпочтительных цифр и их рядов допускаются, если:
- округление до предпочтительного числа выходит за пределы допускаемой погрешности (от плюс 1,26 до минус 1,01 %);
- значения параметров технических объектов следуют закономерности, отличающейся от геометрической прогрессии.
Слайд 15
Основные параметры рядов предпочтительных чисел на основе геометрической
прогрессии
Слайд 16
Предпочтительные числа на основе геометрической прогрессии
В общем
случае следует отдавать предпочтение ряду
с меньшим порядковым
номером. Например, ряд R5
предпочтительнее ряда R10 и т.д.
⃞ В ряд R10 входят все числа ряда R5, в ряд R20 – все
числа рядов R5 и R10, в ряд R40 – все числа рядов
R5, R10 и R20.
Слайд 17
Основные параметры рядов предпочтительных чисел на основе геометрической
прогрессии
Членами рядов предпочтительных чисел являются округленные числа, полученные после
умножения предыдущего числа на знаменатель прогрессии.
Например, в ряде R5 в интервале размеров от 1 до 10 миллиметров имеются следующие предпочтительные числа: 1,0; 1,6; 2,5; 4,0; 6,3; 10,0 мм, а в ряде R10: 1,00; 1,25; 1,60; 2,00; 2,50; 3,15; 4,00; 5,00; 6,30; 8,00;
10,00 мм.
⃞ Ряды предпочтительных чисел безграничны. Числа свыше 10 в каждом десятичном интервале (от 10 до 100, от 100 до 1000 и выше) получают умножением предпочтительных чисел, содержащихся в интервале от 1 до 10, на 10; 100 и т.д.
Слайд 18
Свойства предпочтительных чисел на основе геометрической прогрессии
Количество членов
в каждом десятичном интервале данных прогрессий (1 – 10;
10 – 100; 100 -1000 и т.д., а также 1 – 0,1; 0,1 – 0,01; 0,01 – 0,001 и т.д.) постоянно на протяжении всей прогрессии и равно 5, 10, 20, 40, 80 и 160.
В рядах, кроме ряда R5, содержится число 3,15, приблизительно равное числу , благодаря этому длина окружности и площадь круга, диаметр которого является предпочтительным числом, также являются предпочтительными числами.
Ряд R40 содержит числа 375, 750, 1500 и 3000, которые имеют особое значение в электротехнике, так как они выражают числа оборотов в минуту асинхронных двигателей.
Слайд 19
Свойства предпочтительных чисел на основе геометрической прогрессии
⃞
Произведение или частное двух предпочтительных чисел, а также положительные
или отрицательные степени чисел ряда дают предпочтительное число этого же ряда с относительной ошибкой
в пределах от минус 1,01 до плюс 1,26 %.
Куб любого числа ряда R10 в два раза больше куба предыдущего числа, а квадрат в 1,6 раза больше квадрата предыдущего числа с вышеуказанной ошибкой.
Члены ряда R10 удваивается через каждые три числа ряда.
В любом интервале процент увеличения величины числа является неизменным, недостатком является обязательное округление всех его членов.
Слайд 20
Производные ряды предпочтительных чисел
На основе простейших преобразований геометрической
прогрессии могут быть получены три производных ряда:
-убывающие ряды предпочтительных
чисел:
↓ gi = 10 -i/R (3)
- комплементарные предпочтительные числа:
gi = 10m - 10 -i/R (4)
- арифметические предпочтительные ряды чисел:
аi = а0 ± (10m ·i/R), (5)
при условии, что а0 кратно 10m/R и | аi (10m/R) | ≤ 100.
Слайд 21
Область применения производных предпочтительных чисел
Производные предпочтительные числа устанавливаются
для случаев, в которых из-за естественных закономерностей не могут
быть применены геометрические ряды.
Убывающие ряды положительных предпочтительных чисел применяются для установления значений параметров, приближающихся к нулю, например, загрязнение вещества, риск события и т.п. Эти ряды содержат основные или дополнительные предпочтительные числа. Обозначение убывающего ряда получают добавлением к обозначению каждого основного (дополнительного) ряда предпочтительных чисел знака "↓", например: ↓R5; ↓R40 (300…750).
Слайд 22
Область применения производных предпочтительных чисел
Комплементарные предпочтительные числа следует
использовать для установления параметров, приближающихся к 10m , например,
КПД, вероятность безотказной работы, доверительная вероятность события.
Обозначение комплементарного ряда получают добавлением к обозначению исходного основного (дополнительного) ряда знака "¯", например: Ṝ5.
Слайд 23
Выборочные и составные ряды предпочтительных чисел
ГОСТ 8032-84 предусматривает
образование из полных рядов предпочтительных чисел выборочных и составных
рядов.
Выборочные ряды предпочтительных чисел должны применяться, когда уменьшение числа градаций создает дополнительный эффект, по сравнению с использованием полных рядов. Пример обозначения ряда: R40/3 (используется каждый третий член ряда R40).
Составные ряды предпочтительных чисел получают путем сочетания различных основных и (или) выборочных рядов, например: R10 (2…10) – из основного ряда используются числа от 2 до 10.
Слайд 24
Приближенные предпочтительные числа
Приближенные предпочтительные числа получают путем округления
чисел основного ряда и используют в обоснованных случаях. Примеры
таких чисел
(в скобках – соответствующие числа основных рядов):
R"5: 1,5 (1,6) и 6,0 (6,3);
R"10: 3,20 (3,15), т.е ряд идентичен ряду R10, кроме числа 3,20.
⃞ Приближенные предпочтительные из ряда R40 легли в основу построения нормальных линейных размеров по ГОСТ 6636-69. Значит, считая от 1 мм, размеры увеличиваются в 1,06 раз. Их можно представить в виде: 1,00; 1,06; 1,12; 1,19; 1,26; 1,34 (с округлениями) и т.д.
Слайд 25
Специальные ряды чисел
Специальные ряды чисел применяются в тех
случаях, когда ни один вид регламентированных чисел не может
быть применен.
Примеры специальных рядов чисел приведены в таблице 1.
Слайд 26
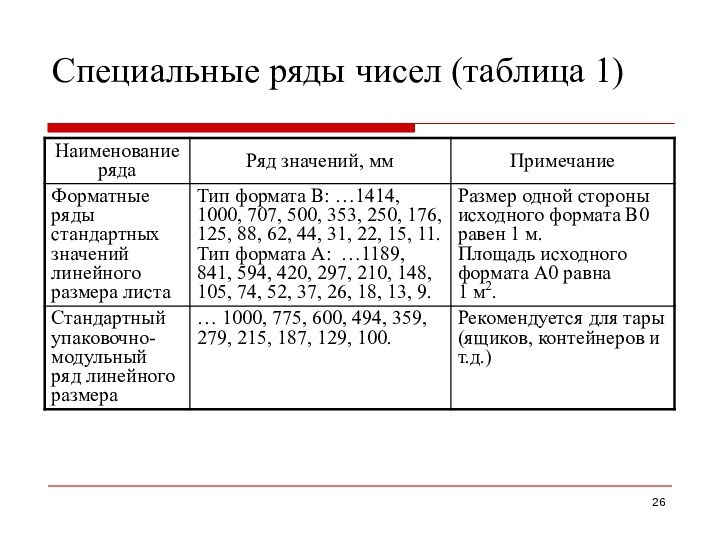
Специальные ряды чисел (таблица 1)
Слайд 27
Специальные ряды чисел (таблица 1)