Слайд 2
Взаимное расположение прямых в пространстве.
Прямые в пространстве могут
совпадать,
быть параллельными, пересекаться или
скрещиваться.
Две прямые L1
и L2 лежат в одной плоскости
тогда и только тогда, когда компланарны
векторы , где -
направляющие векторы прямых L1 и L2,
соответственно, а - вектор,
соединяющий точку М1, лежащую на прямой
L1, с точкой М2, лежащей на прямой L2.
Слайд 3
Следовательно, если смешанное
произведение векторов
равно
нулю, то прямые лежат в одной плоскости.
Если прямые принадлежат одной плоскости,
то они могут совпадать, пересекаться и быть
параллельными.
Пусть заданы прямые L1 и L2:
Слайд 4
где М1(x1, y1, z1) L1 , М2(x2, y2,
z2) L2, а
и
– направляющие векторы прямых L1 и L2, соответственно:
Тогда прямые L1 и L2:
1) скрещиваются, если
Слайд 5
2) пересекаются, если
и вектор
не коллинеарен вектору , т. е.
координаты
этих векторов не
пропорциональны:
или
Слайд 6
3) параллельны, если
и точка М1(x1, y1, z1) L2, то
есть
Слайд 7
4) совпадают, если
и точка М1(x1, y1, z1) L2, то
есть
Слайд 8
Угол между прямыми в пространстве
Пусть
где
- направляющие векторы прямых L1 и L2.
Слайд 9
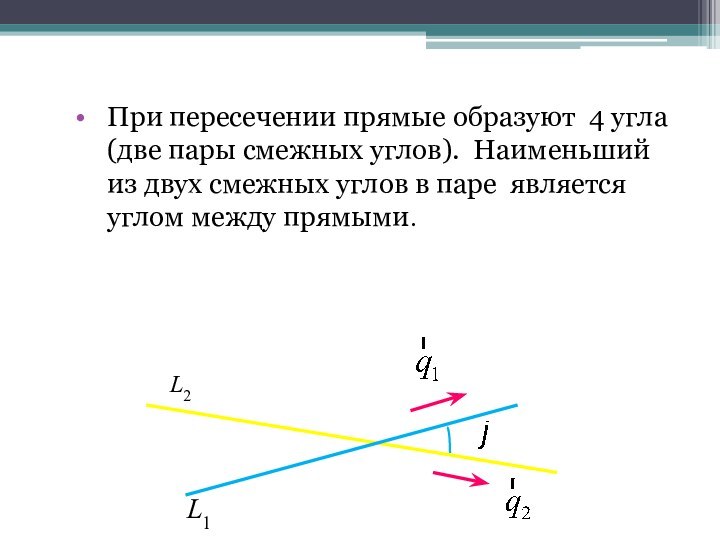
При пересечении прямые образуют 4 угла (две пары
смежных углов). Наименьший из двух смежных углов в паре
является углом между прямыми.
L2
L1
Слайд 10
Косинус наименьшего угла между прямыми L1 и L2
равен модулю косинуса угла между направляющими векторами этих прямых:
Слайд 11
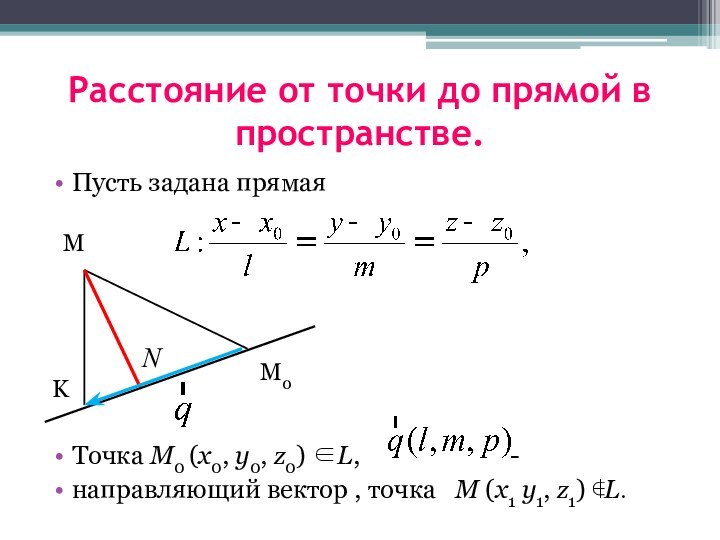
Расстояние от точки до прямой в пространстве.
Пусть задана
прямая
Точка M0 (x0, y0, z0) L,
-
направляющий вектор , точка M (x1 y1, z1) L.
N
M
K
M0
к точке M0. Тогда расстояние от точки
М до прямой L равно высоте треугольника MKM0.
Тогда расстояние от точки М до прямой L можно найти по формуле:
Слайд 13
Замечание.
Расстояние между параллельными прямыми может быть найдено по
этой же формуле, как расстояние от любой точки, принадлежащей
одной прямой, до другой прямой.
Слайд 14
Расстояние между скрещивающимися прямыми в пространстве.
Пусть
где М1(x1, y1,
z1) L1 , М2(x2, y2, z2) L2, а
, - направляющие векторы прямых L1 и L2 .
Тогда
Слайд 15
Тогда расстояние между скрещивающимися прямыми можно найти по
формуле:
где
- модуль смешанного произведения векторов, а - модуль векторного произведения.
Слайд 16
Взаимное расположение прямой и плоскости в пространстве.
Пусть в
пространстве заданы прямая
и
Слайд 17
Точка M0(x0,y0,z0)L , вектор
– направляющий вектор прямой L; вектор
– нормальный вектор плоскости Р.
Прямая может пересекать плоскость, быть ей параллельной или лежать в плоскости.
1. Если прямая лежит в плоскости, то
и точка М(x0, y0, z0) P. Таким
образом, прямая лежит в плоскости,
если: Al + Bm + Cp = 0 и
Слайд 18
2. Если прямая параллельна плоскости,
то
и точка М(x0, y0, z0) P.
Таким
образом, прямая параллельна
плоскости, если: Al + Bm + Cp = 0 и
3. Прямая пересекает плоскость, если направляющий вектор прямой не перпендикулярен нормальному вектору плоскости, а значит их скалярное произведение не равно нулю: , т. е. Al + Bm + Cp 0.
Слайд 19
Угол между прямой и плоскостью.
Углом между прямой и
плоскостью называется угол между прямой и ее проекцией на
эту плоскость.
Рассмотрим прямую
и плоскость