- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Раздел 2. Дифференциальное исчисление функций одной переменной
Содержание
- 2. Два подхода к понятию дифференцируемой функции и их равносильность. Непрерывность дифференцируемой функции.
- 3. Два подхода к понятию дифференцируемой функции и их равносильность. Непрерывность дифференцируемой функции.
- 4. Два подхода к понятию дифференцируемой функции и их равносильность. Непрерывность дифференцируемой функции.
- 5. Два подхода к понятию дифференцируемой функции и их равносильность. Непрерывность дифференцируемой функции.
- 6. 2. Правила дифференцирования суммы, произведения, частного.
- 7. 3. Правило дифференцирования сложной функции. Логарифмическое дифференцирование.
- 8. 3. Правило дифференцирования сложной функции. Логарифмическое дифференцирование.
- 9. 4. Правило дифференцирования обратной функции.
- 10. 5. Производные основных элементарных функций.
- 11. 6. Функции, заданные параметрически, и их дифференцирование.
- 12. 7. Функции, заданные неявно, и их дифференцирование.
- 13. 7. Функции, заданные неявно, и их дифференцирование.3
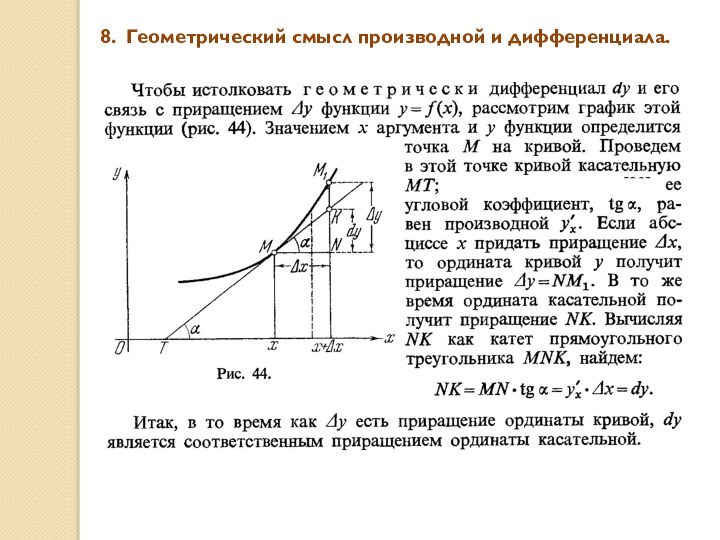
- 14. 8. Геометрический смысл производной и дифференциала.
- 15. Пусть каждому значению поставлен в соответствие
- 16. 10. Производные и дифференциалы высших порядков. Правило Лейбница.
- 17. 10. Производные и дифференциалы высших порядков. Правило Лейбница.
- 18. 10. Производные и дифференциалы высших порядков. Правило Лейбница.
- 19. 10. Производные и дифференциалы высших порядков. Правило Лейбница.
- 20. 10. Производные и дифференциалы высших порядков. Правило Лейбница.
- 21. Скачать презентацию
- 22. Похожие презентации
Два подхода к понятию дифференцируемой функции и их равносильность. Непрерывность дифференцируемой функции.



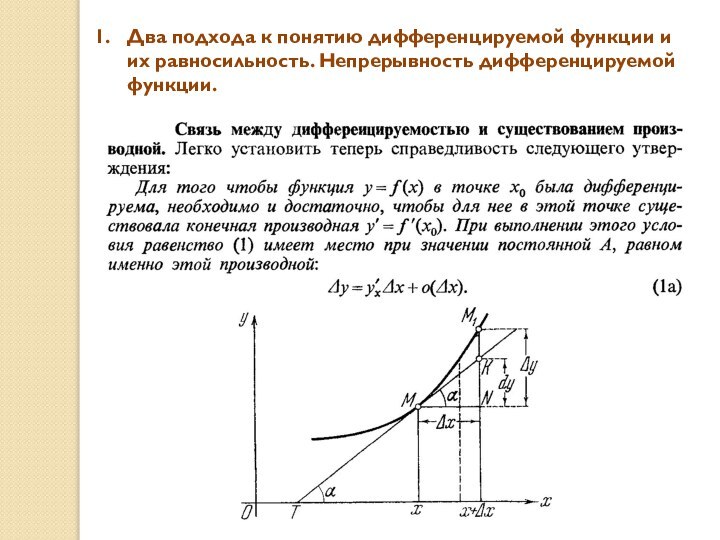
















Слайд 2 Два подхода к понятию дифференцируемой функции и их
равносильность. Непрерывность дифференцируемой функции.
Слайд 3 Два подхода к понятию дифференцируемой функции и их
равносильность. Непрерывность дифференцируемой функции.
Слайд 4 Два подхода к понятию дифференцируемой функции и их
равносильность. Непрерывность дифференцируемой функции.
Слайд 5 Два подхода к понятию дифференцируемой функции и их
равносильность. Непрерывность дифференцируемой функции.
Слайд 15 Пусть каждому значению поставлен в соответствие вектор
трехмерного пространства. В этом случае говорят, что на
множестве D задана векторная функция.Если в пространстве задана декартова система координат, то задание вектор-функции означает задание скалярных функций x (t), y (t), z (t).
9. Вектор-функции и их дифференцирование.





























