Слайд 2
Під нарощеною сумою позики (довга, депозиту, інших видів
виданих у борг або інвестованих грошей) розуміють первинну її
суму з нарахованими відсотками до кінця терміну нарахування.
Нарощена сума визначається множенням первинної суми боргу на множник нарощування, який показує, в скільки разів нарощена сума більше первинної. Розрахункова формула залежить від виду вживаної процентної ставки і умов нарощування.
Слайд 3
Для запису формули нарощування простих відсотків приймемо позначення:
I
— відсотки за весь термін позики;
Р — первинна сума
боргу;
S — нарощена сума, тобто сума в кінці терміну;
i — ставка нарощування відсотків (десятковий дріб);
п — термін позики.
Якщо термін вимірюється в роках (як це звичайно і буває), то i означає річну процентну ставку. Відповідно кожний рік приносить відсотки в сумі Pi. Нараховані за весь термін відсотки складуть
I = Pni
Нарощена сума, таким чином, знаходиться як
S = Р + I = Р + Pni = P(1+ ni)
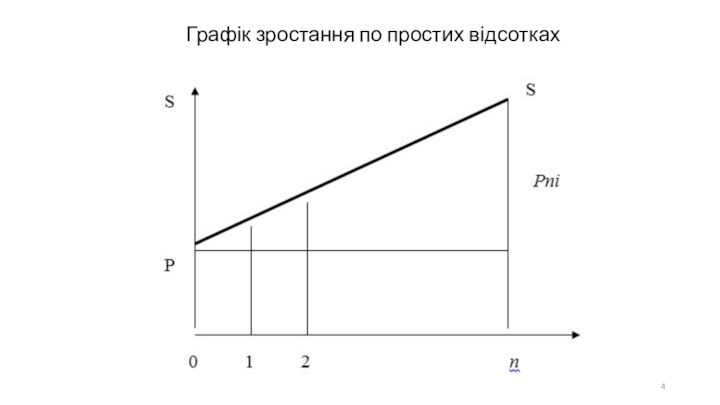
Слайд 4
Графік зростання по простих відсотках
Слайд 5
ПРИКЛАД
Визначимо відсотки і суму накопиченого боргу, якщо
позика дорівнює 700 тис.грн., термін 4 року, відсотки прості
по ставці 20% річних:
Р=700 тис. грн.
n=4 роки
i=0,2
I = 700 х 4 х 0,2 = 560 тис. грн.;
S = 700 + 560 = 1260 тис. грн.
Слайд 6
Практика розрахунку відсотків для короткострокових позик
Розглянемо найбільш поширений
в практиці випадок — з річними періодами нарахування. Очевидно,
що термін позики необов'язково рівний цілому числу років. Виразимо термін n у вигляді дробу
,
де t — число днів позики, К — число днів в році, або тимчасова база нарахування відсотків.
Слайд 7
При розрахунку відсотків застосовують дві тимчасові бази: К
= 360 днів (12 місяців по 30 днів) або
К = 365, 366 днів.
Отже, можливі і застосовуються на практиці три варіанти розрахунку простих відсотків.
1. Точні відсотки з точним числом днів позики. Цей варіант, природно, дає найточніші результати. Даний спосіб застосовується центральними банками багатьох країн і крупними комерційними банками, наприклад, у Великобританії, США. В комерційних документах він позначається як 365/365 або ACT/ACT.(Англійський)
Слайд 8
2. Звичайні відсотки з точним числом днів позики.
Цей метод, іноді називають банківським, поширений у Франції, Бельгії,
Швейцарії. Він позначається, як 365/360 або АСТ/360. Цей варіант дає дещо більший результат, ніж застосування точних відсотків. Помітимо, що при числі днів позики, що перевищує 360, даний спосіб призводить до того, що сума нарахованих відсотків буде більше, ніж передбачається річною ставкою. Наприклад, якщо t = 364, то п = 364/360 = 1,01111. Множник нарощування за рік за умови, що i = 20%, складе 1,20222. (Французький)
3. Звичайні відсотки з наближеним числом днів позики. Такий метод застосовується тоді, коли не вимагається великої точності, наприклад при проміжних розрахунках. Він прийнятий в практиці комерційних банків Німеччини, Швеції, Данії. Метод умовно позначається як 360/360.(Німецький)
Слайд 9
ПРИКЛАД
Позика у розмірі 1 млн грн. видана
20.01 до 05.10 включно під 18% річних. Яку суму
повинен заплатити боржник в кінці терміну при нарахуванні простих відсотків? При рішенні застосуємо всі три методи. Заздалегідь визначимо число днів позики: точне — 258, наближене — 255.
1. Точні відсотки з точним числом днів позики (365/365):
S = 1 000 000(1+ 0,18)= 1 127 233 грн.
2. Звичайні відсотки з точним числом днів позики (365/360):
S = 1 000 000(1 + 0,18)= 1 129 000 грн.
3. Звичайні відсотки з наближеним числом днів позики (360/360):
S = 1 000 000(1 + 0,18)= 1 127 500 грн.
Слайд 10
Дисконтування по простих процентних ставках
У фінансовій практиці часто
виникають задачі, зворотні нарощуванню відсотків: по заданій сумі S,
яку слід сплатити через деякий час п, необхідно визначити суму отриманої позики Р.
Така ситуація може виникнути, наприклад, при розробці умов контракту. Розрахунок Р по S необхідний і тоді, коли відсотки з суми S утримуються вперед, тобто безпосередньо при видачі кредиту, позики. В цих випадках говорять, що сума S дисконтується або враховується, сам процес нарахування відсотків і їх утримання називають обліком, а утримані відсотки — дисконтом або знижкою.
Необхідність дисконтування виникає, наприклад, при покупці короткострокових зобов'язань, оплата яких боржником відбудеться в майбутньому.
Слайд 11
Величину Р, знайдену за допомогою дисконтування, називають сучасною
вартістю, або сучасною величиною, майбутнього платежу S, а іноді
— поточною, або капіталізованою, вартістю. Сучасна величина суми грошей є одним з найважливіших понять в кількісному аналізі фінансових операцій. В більшості випадків саме за допомогою дисконтування, а не нарощування, зручно враховувати такий чинник, як час. Як буде показано далі, більшість аналітичних методів ґрунтується на визначенні сучасної величини платежів.
Залежно від виду процентної ставки застосовують два методи дисконтування — математичне дисконтування і банківський (комерційний) облік. В першому випадку застосовується ставка нарощування, в другому — облікова ставка.
Слайд 12
Математичне дисконтування
Математичне дисконтування є рішенням задачі, зворотної
нарощуванню первинної суми позики. Задача в цьому випадку сформулюється
так: яку первинну суму позики треба видати в борг, щоб отримати в кінці терміну суму S, за умови, що на борг нараховуються відсотки по ставці i?
Знаходимо
S = Р + I = Р + Pni = P(1+ ni).
P =
Нагадаємо, що n = t/K — термін позики в роках.
Встановлена таким шляхом величина Р є сучасною величиною суми S, яка буде виплачена через n років.
Слайд 13
Банківський облік (облік векселів)
Суть операції полягає в наступному.
Банк або інша фінансова установа до настання терміну платежу
по векселю або іншому платіжному зобов'язанню придбає його у власника за ціною, яка менше суми, вказаної на векселі, тобто купує (враховує) його з дисконтом. Отримавши при настанні терміну векселя гроші, банк реалізує процентний дохід у вигляді дисконту. У свою чергу власник векселя за допомогою його обліку має нагоду отримати гроші хоча і не в повному об'ємі, проте раніше вказаного на ньому терміну.
При обліку векселя застосовується банківський, або комерційний, облік. Згідно цьому методу відсотки за користування позикою у вигляді дисконту нараховуються на суму, що підлягає сплаті в кінці терміну. При цьому застосовується облікова ставка d.
Слайд 14
Розмір дисконту, або суми обліку: D=Snd або D=S-P;
якщо d — річна облікова ставка, то n вимірюється
в роках. Таким чином
Р= S- Snd= S(1 - nd)
де n — термін від моменту обліку до дати погашення векселя.
З формули витікає, що при n > 1/d величина дисконтного множника і, отже, суми Р стане негативною. Інакше кажучи, при відносно великому терміні векселя облік може привести до нульової або навіть негативної суми Р. Наприклад, при d = 20% вже п'ятирічний термін достатній для того, щоб власник векселя нічого не отримав при його обліку.
Облік за допомогою облікової ставки частіше за все здійснюється при тимчасовій базі К = 360 днів, число днів позики звичайно береться точним, АСТ/360.
Слайд 15
ПРИКЛАД
Тратта (переказний вексель) видана на суму 1
млн грн. із сплатою 17.11.2014р. Власник векселя врахував його
в банку 23.09.2014р. по обліковій ставці 20% (АСТ/360). До кінця терміну залишилося:
t = 321-266 = 55 днів.
Отримана при обліку сума (без сплати комісійних) дорівнює:
P = S(1 - nd) =1000000(1 – 0,2) = 969444,4 грн.
Дисконт складе D=S-P = 1000000 - 969444,4 = 30555,6 грн.
Слайд 16
Складні процентні ставки
Нарахування складних
річних відсотків
Слайд 17
Формула нарощування
В середнє- і довгострокових фінансово-кредитних операціях, якщо
відсотки не виплачуються одразу після їх нарахування, а приєднуються
до суми боргу, застосовують складні відсотки.
Знайдемо формулу для розрахунку нарощеної суми за умови, що відсотки нараховуються і капіталізуються один раз в році (річні відсотки). Для цього застосовується складна ставка нарощування. Для запису формули нарощування застосуємо ті ж позначення, що і у формулі нарощування по простих відсотках:
Р — первинний розмір боргу (позики, кредиту, капіталу і т.д.)
S — нарощена сума на кінець терміну позики
п — термін, число років нарощування
i — рівень річної ставки відсотків, представлений десятковим дробом.
Слайд 18
ПРИКЛАД
Якої величини досягне борг, рівний 1 млн
грн. через 5 років при зростанні по складній ставці
15,5% річних?
S = 1000000(1 + 0.155)5 = 2055464,22 грн.
Причому із загальної суми нарахованих відсотків, Iр = 280464,22 грн. доводиться на відсотки на відсотки. Час при нарощуванні по складній ставці звичайно вимірюється як ACT/ ACT.
Слайд 19
Острів Манхеттен, на якому розташована центральна частина Нью-Йорка,
був куплений (а точніше виміняний) за 24 долл. Вартість
землі цього острова через 350 років оцінювалася приблизно в 40 млрд долл. Таке зростання досягається при складній ставці, рівній всього 6,3 % річних.
Слайд 20
Нарахування відсотків при дробовому числі років
Часто термін
в роках для нарахування відсотків не є цілим числом.
В правилах ряду комерційних банків для деяких операцій відсотки нараховуються тільки за ціле число років або інших періодів нарахування. Дробова частина періоду відкидається. В більшості ж випадків враховується повний термін. При цьому застосовують два методи. Згідно першого, назвемо його загальним, розрахунок ведеться безпосередньо по формулі:
S = P(1 + i)ⁿ
Другий, змішаний, метод припускає нарахування відсотків за ціле число років по формулі складних відсотків і за дробову частину терміну по формулі простих відсотків:
Де n=a+b – термін позики, а –ціле число років, b – дробова частина року.
Слайд 22
Дисконтування по складній ставці
При вивченні простих відсотків ми
розглядали математичне дисконтування і банківський (комерційний) облік. Перше полягало
у визначенні Р по значенню S при заданій ставці відсотка, друге — при заданій обліковій ставці. Застосуємо перший метод і дисконтуємо тепер суму S по складній ставці відсотків.
Для випадків, коли відсотки нараховуються т раз в році, отримаємо
Слайд 23
Нагадаємо, що величину Р, отриману дисконтуванням S, називають
сучасною, поточною вартістю, або сучасною величиною S.
Сучасна вартість
може бути розрахована на будь-який момент до виплати суми S.
Різниця S — Р, у разі, коли Р визначено дисконтуванням, називають дисконтом. Позначимо останній через D.
D = S - Р
ПРИКЛАД 8
Сума в 5 млн грн. виплачується через 5 років. Необхідно визначити її сучасну величину за умови, що застосовується ставка складних відсотків, яка дорівнює 12% річних.
Сучасна величина дорівнює
Р = 5000 х 1,12-5 = 2837,1 тис. грн.
Слайд 25
ПРИКЛАД 9
Боргове зобов’язання 5 тис.грн. термін оплати якого
наступає через 5 років, продано з дисконтом за складною
обліковою ставкою 15% річних. Який розмір отриманої за борг суми і величина дисконту?
Р = 5000 (1 – 0,15)⁵ = 2218,5;
D = 5000 – 2218,5 = 2781,5.
Якщо застосувати просту облікову ставку того ж розміру, то
Р = 5000 (1 - 5 х 0,15) = 1 250;
D = 5000 - 1250 = 3750.
Слайд 26
Еквівалентність процентних ставок
Як було показано раніше, для процедур
нарощування і дисконтування можуть застосовуватися різні види процентних ставок.
Визначимо тепер ті їх значення, які в конкретних умовах приводять до однакових фінансових результатів.
Інакше кажучи, заміна одного виду ставки на іншій при дотриманні принципу еквівалентності не змінює фінансових відносин сторін в рамках однієї операції.
Такі ставки, при яких результати нарощення або дисконтування будуть однакові, назвемо еквівалентними.
Слайд 27
Визначимо співвідношення еквівалентності між простою і складною ставками.
Для цього прирівняємо один до одного відповідні множники нарощування:
(1
+ nis) = (1 + i)n,
де is і i — ставки простих і складних відсотків.
Рішення приведеної вище рівності дає наступні співвідношення еквівалентності:
Слайд 31
Потоки платежів.
Види потоків платежів і їх основні параметри
Слайд 32
Сучасні фінансово-банківські операції часто передбачають не окремі або
разові платежі, а деяку їх послідовність в часі, наприклад,
погашення заборгованості в розстрочку, періодичне надходження доходів від інвестицій, виплати пенсії і т.д.
Такого роду послідовність виплат, або ряд платежів, називають потоком платежів.
Окремий елемент такого ряду платежів назвемо членом потоку.
Потоки платежів можуть бути регулярними (розміри платежів постійні або слідують встановленому правилу, що передбачає рівні інтервали між платежами) і нерегулярними. Члени потоків можуть бути як позитивними (надходження), так і негативними величинами (виплати).
Потік платежів, всі члени якого — додатні величини, а інтервали між платежами однакові, називають фінансовою рентою або просто рентою.
Іноді подібного роду потік платежів називають ануїтетом, що, строго кажучи, застосовно тільки до щорічних виплат.
Слайд 33
В практиці застосовують різні ренти. В основу їх

класифікації може бути встановлений ряд ознак. Розглянемо деякі з
таких класифікацій.
По кількості виплат членів ренти протягом року ренти діляться на річні (виплата раз в році) і р-термінові (р — кількість виплат в році).
У фінансовій практиці зустрічаються і з такими послідовностями платежів, які проводяться так часто, що їх практично можна розглядати як безперервні.
По числу раз нарахувань відсотків протягом року розрізняють: ренти з щорічним нарахуванням, з нарахуванням т раз в році, з безперервним нарахуванням. Моменти нарахування відсотків необов'язково співпадають з моментами виплат членів ренти. Проте, як буде показано, розрахунки помітно спрощуються, якщо два вказані моменти співпадають.
По величині своїх членів ренти діляться на постійні (з однаковими розмірами члена ренти) і змінні. Члени змінних рент змінюють свої розміри в часі, слідуючи якому-небудь закону, наприклад арифметичної або геометричної прогресії, або несистематично (задаються таблицею). Постійні ренти — найпоширеніший вид ренти.
Слайд 34
По ймовірності виплат ренти діляться на вірні і

умовні. Вірні ренти підлягають безумовній сплаті, наприклад, при погашенні
кредиту. Число членів такої ренти заздалегідь відоме. У свою чергу виплата умовної ренти ставиться в залежність від настання деякої випадкової події, число її членів заздалегідь невідомо.
По кількості членів розрізняють ренти з кінцевим числом членів, або обмежені ренти (їх термін заздалегідь обумовлений), і нескінченні, або вічні ренти. З вічною рентою зустрічаються на практиці у ряді довгострокових операцій, коли передбачається, що період функціонування аналізованої системи або термін операції вельми тривалий і не обмовляється конкретними датами.
По співвідношенню початку терміну ренти і якого-небудь моменту часу, що попереджує початок ренти (наприклад, початок дії контракту або дати його висновку), ренти діляться на негайні і відкладені, або відстрочені. Приклад відстроченої ренти: погашення боргу в розстрочку після пільгового періоду.
Дуже важливою є відмінність по моменту виплат платежів в межах періоду ренти. Якщо платежі здійснюються в кінці цих періодів, то відповідні ренти називають звичайними, або, якщо ж платежі проводяться на початку періодів, то їх називають пренумерандо. Іноді контракти передбачають платежі або надходження грошей в середині періодів.
Слайд 36
ПРИКЛАД
Для забезпечення деяких майбутніх витрат створюється фонд.
Засоби до фонду поступають у вигляді постійної річної ренти
постнумерандо протягом 5 років. Розмір разового платежу 4 млн. грн. На внески, що поступили, нараховуються відсотки по ставці 18,5% річних. Величина фундації на кінець терміну складе
млн. грн.
Слайд 37
Річна рента постнумерандо (m=p=1)
Річна рента постнумерандо, нарахування відсотків т раз в році
Рента p-термінова (т = 1)
Слайд 38
Рента p-термінова (р = m)
Рента р-термінова (р ≠
т)