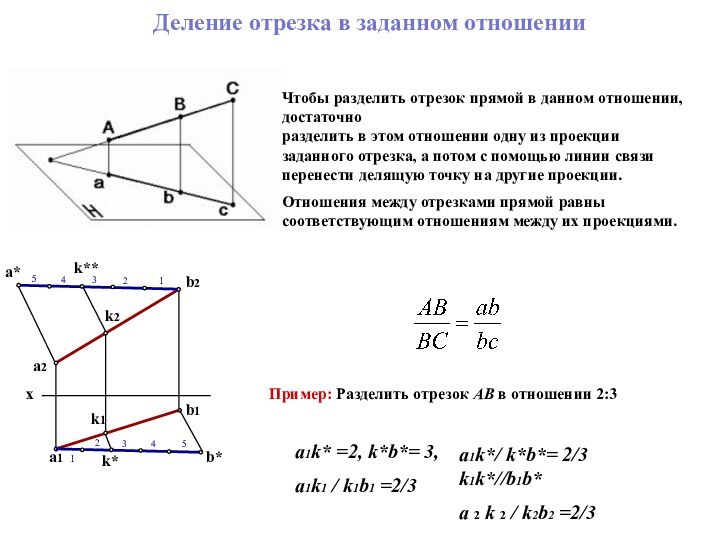
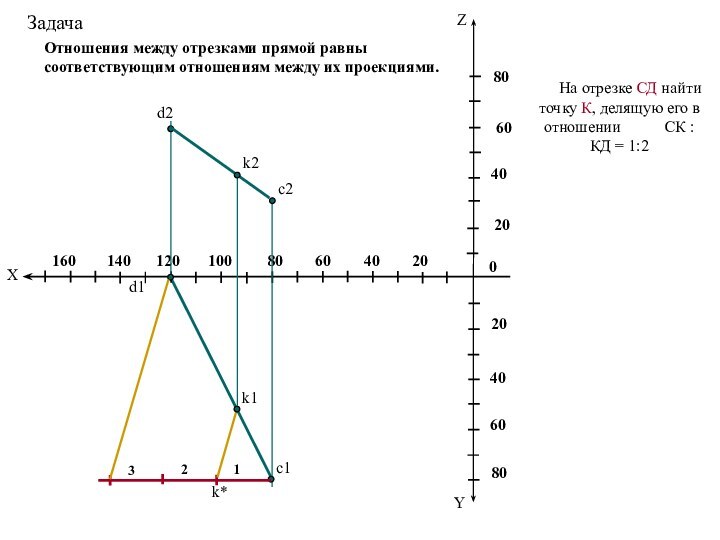
прямой. Деление отрезка прямой линии в заданном отношении.
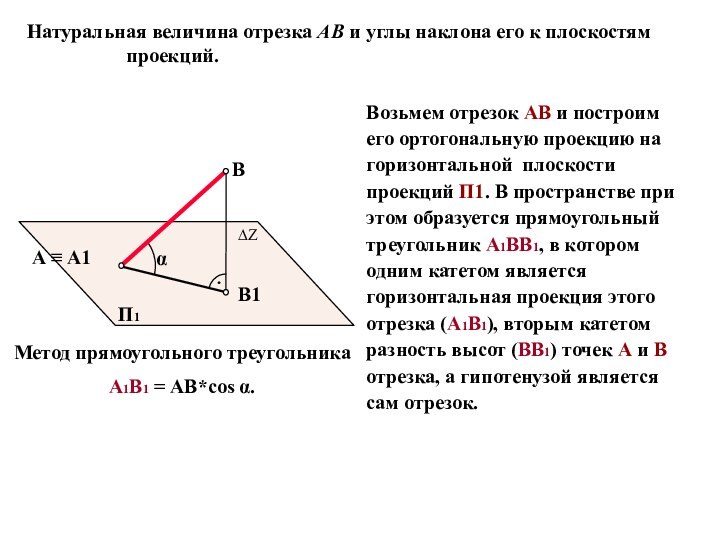
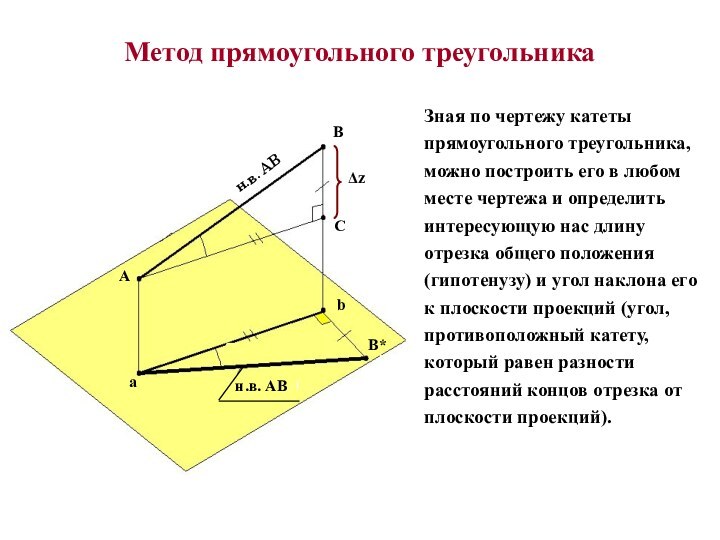
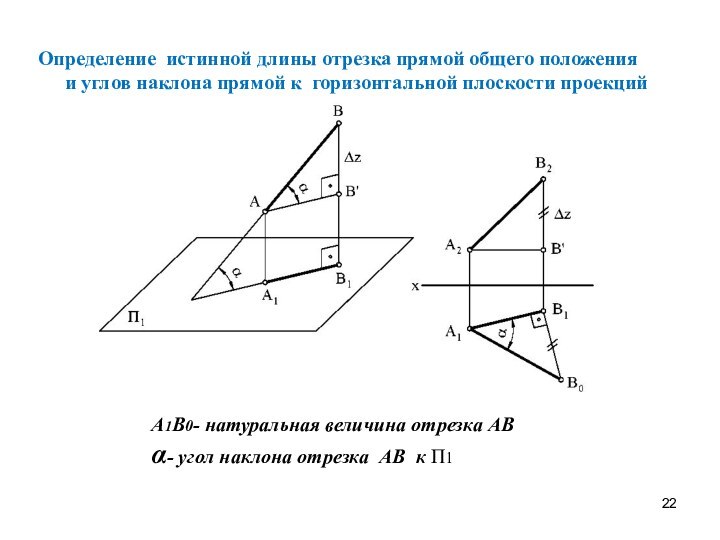
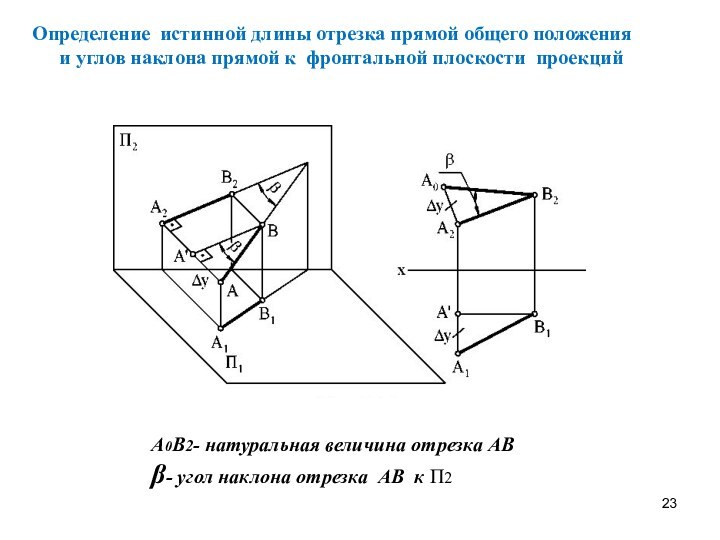
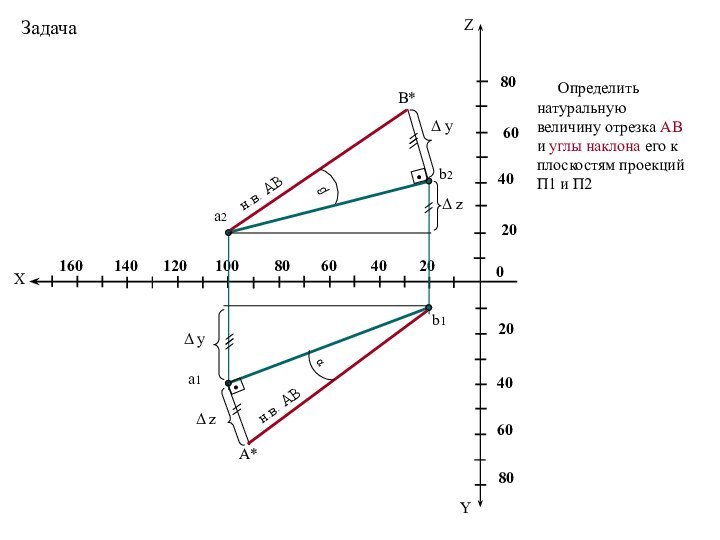
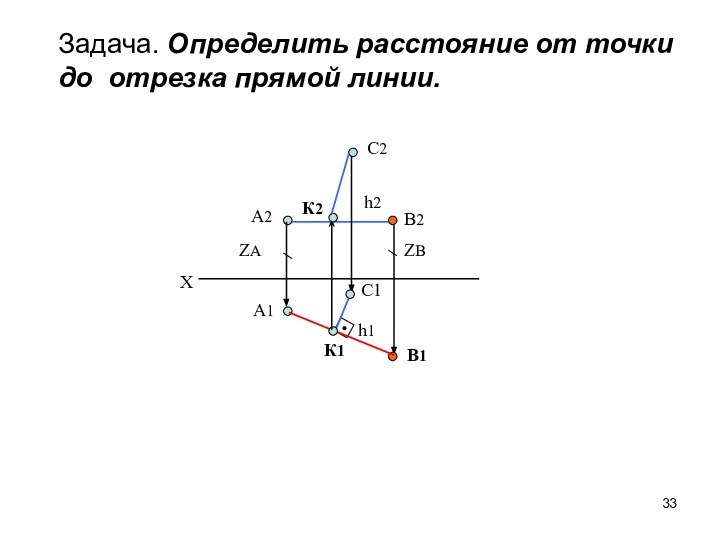
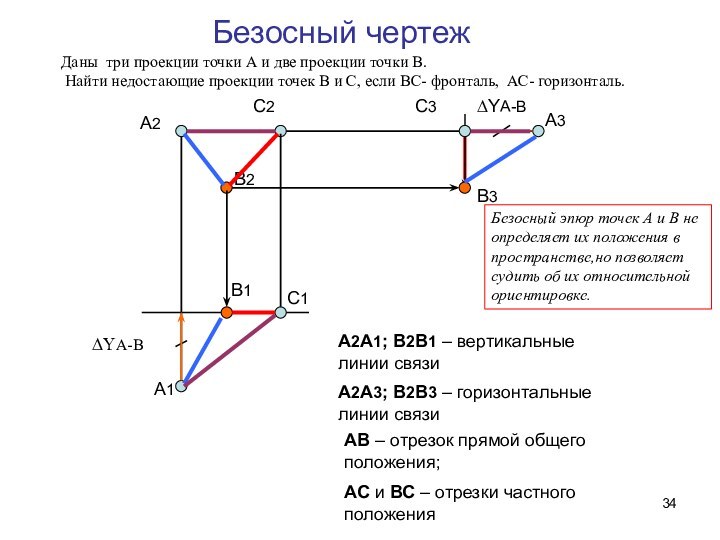
Определение длины
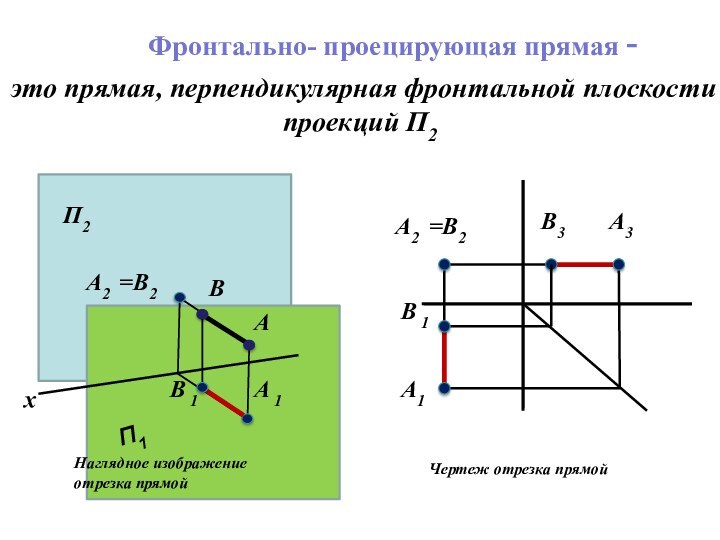
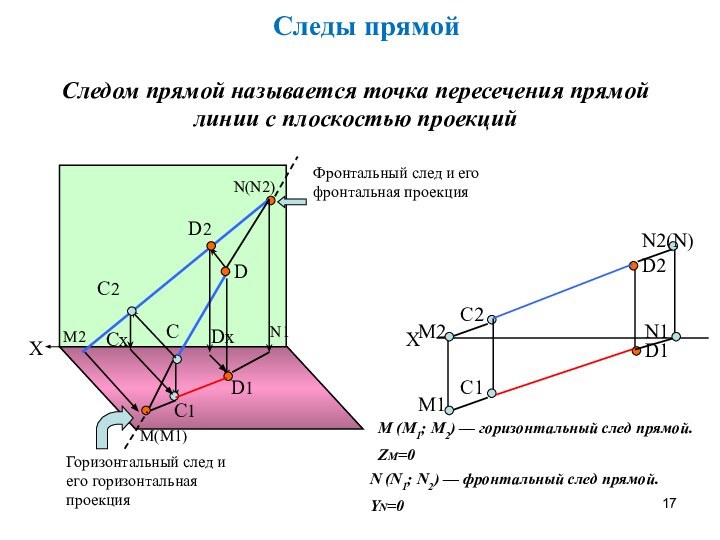
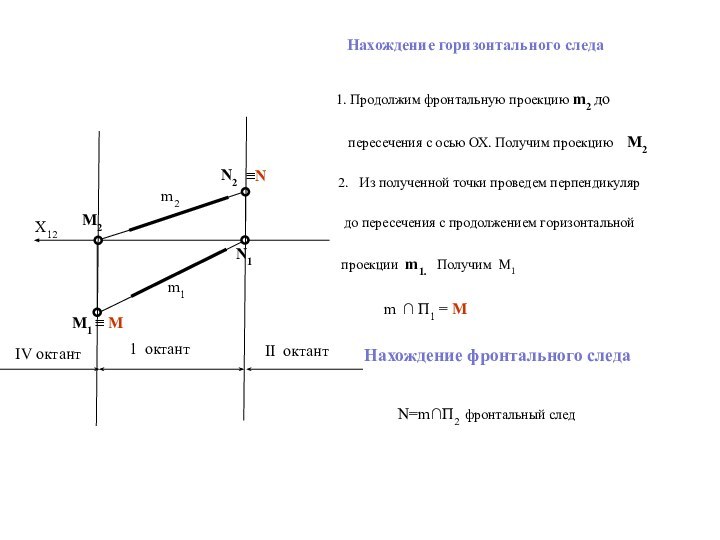
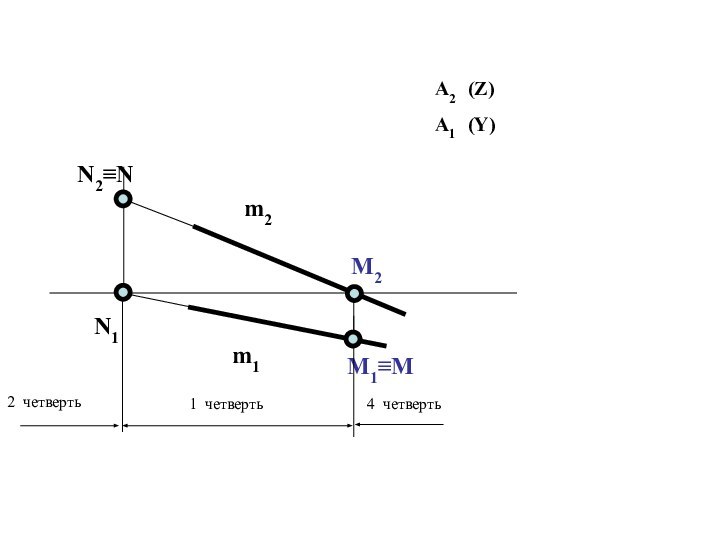
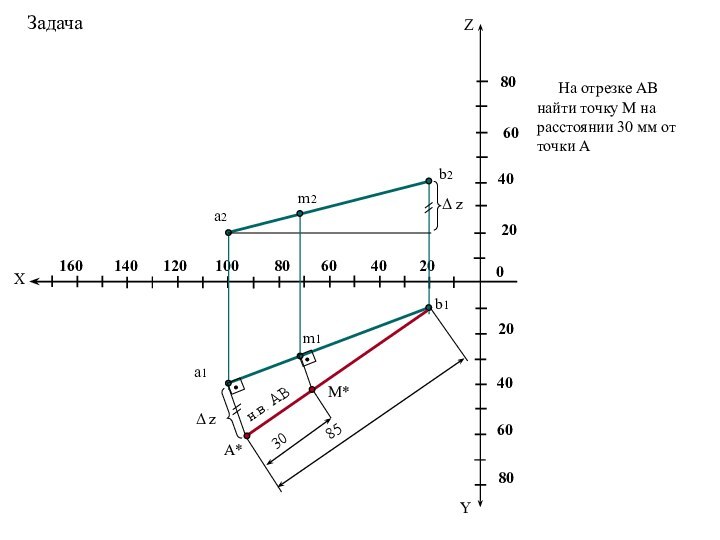
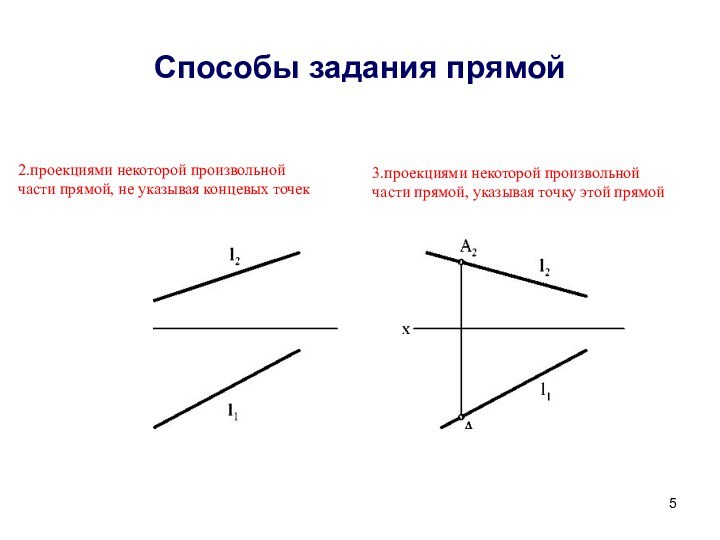
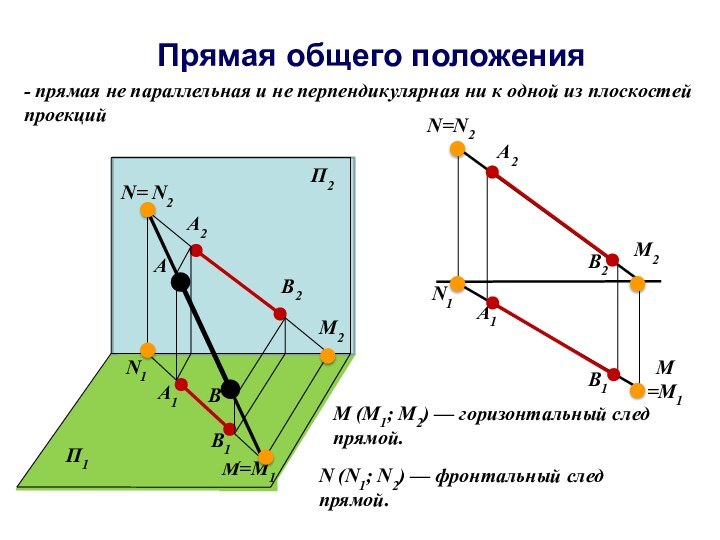
отрезка прямой общего положения и углов наклона прямой к плоскостям проекций.Следы прямой линии.
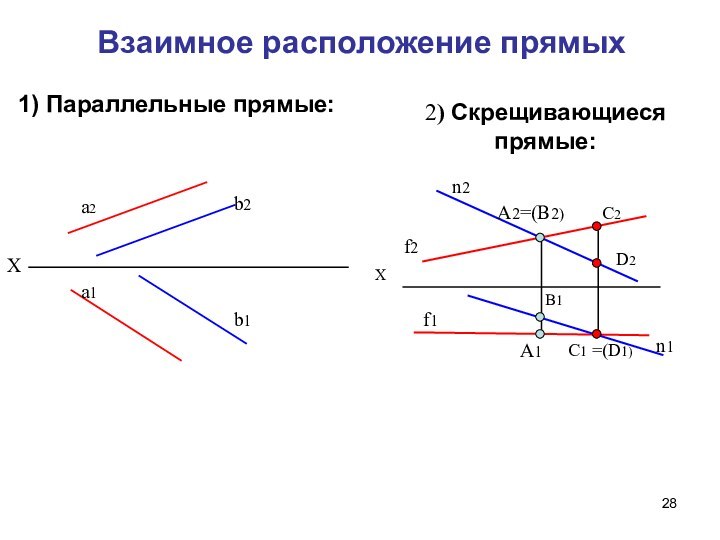
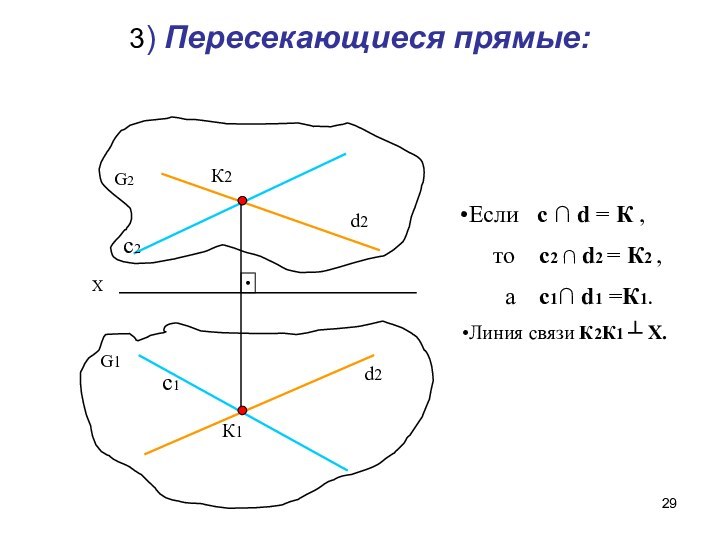
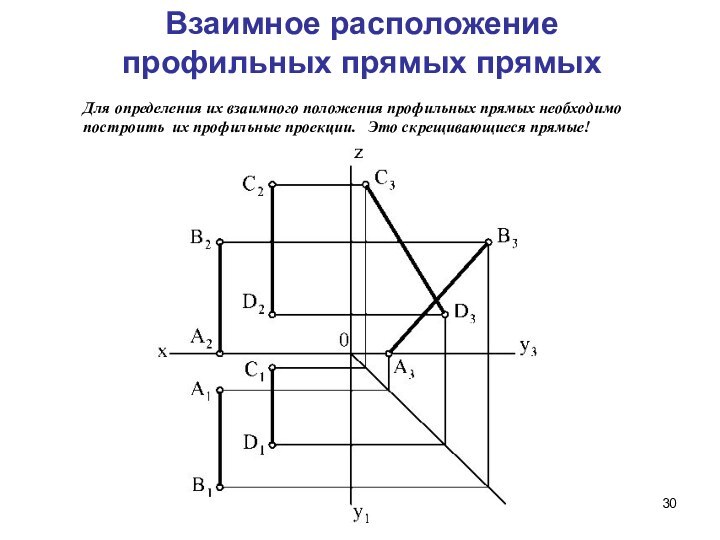
Взаимное положение прямых.
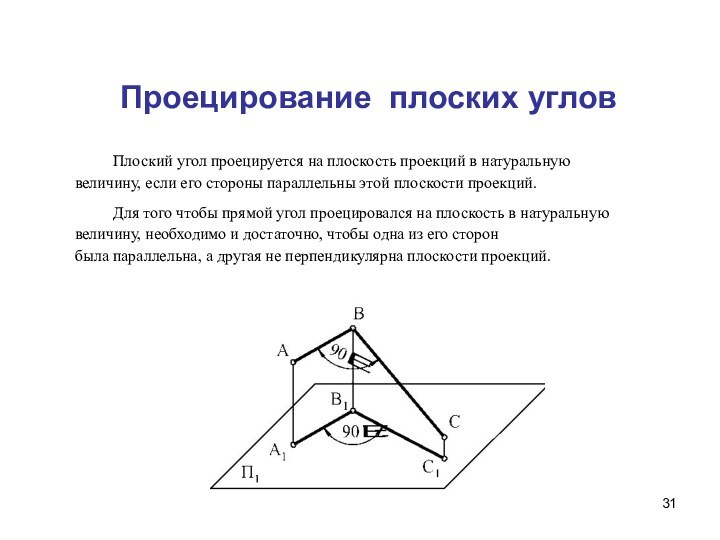
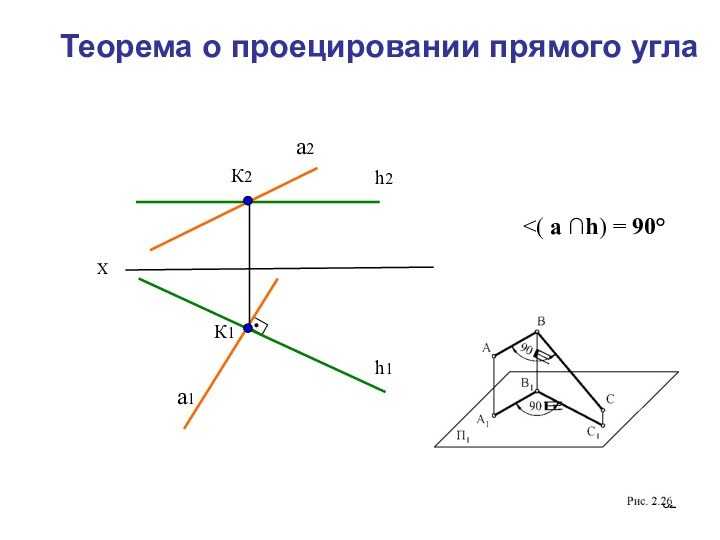
Проекции плоских углов.


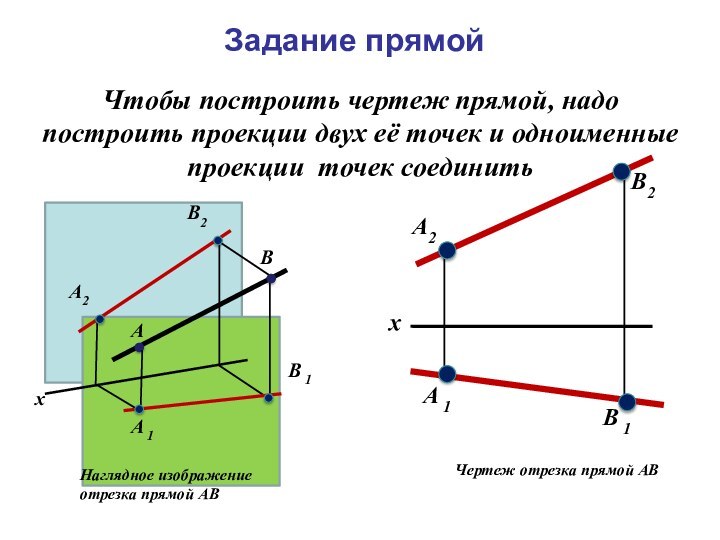
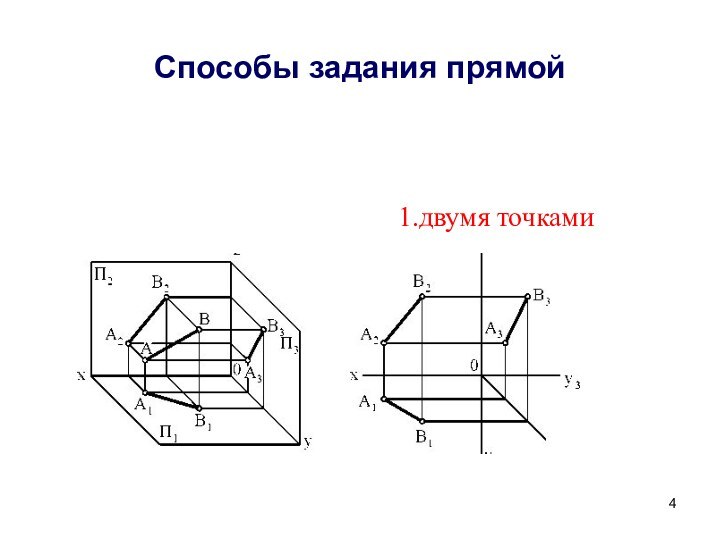

![Прямая E1C1D1ХZYA2YХYZYВ2В1A1С2D2K1L1K2L2M2N2M1N1M3N3E2F2F1H2S2H1S1P2R2P1R1P3R3[АВ] прямая общего положения [CD] горизонтально-](/img/tmb/14/1347277/217e1a8bcaf46ffa4999881cfcc4e960-720x.jpg)