- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Растяжение и сжатие
Содержание
- 2. Определение нормальных усилий и напряжений. Построение эпюрРастяжение
- 3. Рассмотрим двухступенчатый стержень, нагруженный системой сил
- 4. Для определения внутренних усилий (продольных сил) применим
- 5. Участок 2-3 , 2а ≤ x1 ≤
- 6. Участок 3-4 , 3а ≤ x3 ≤
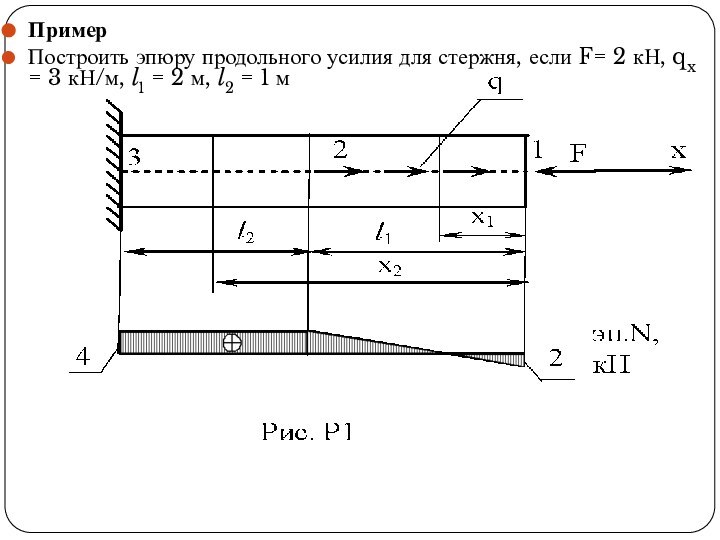
- 7. ПримерПостроить эпюру продольного усилия для стержня, если
- 8. Участок 1-2, 0≤x1 ≤l1N1=qx1–FX1=0, N1=-2кН; x1=l1=2м, N1=4кН.Участок 2-3, l2 ≤x2 ≤l1+ l2N2=ql1–F=4кН
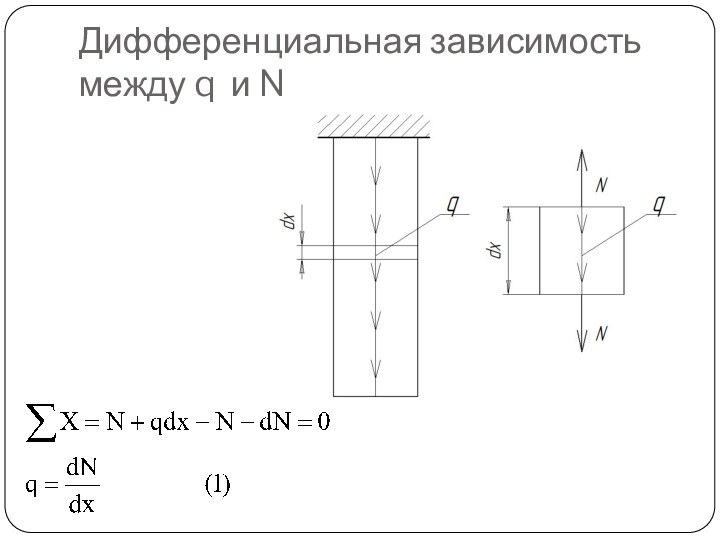
- 9. Дифференциальная зависимость между q и N
- 10. Свойства эпюр N С учётом выражения (1)
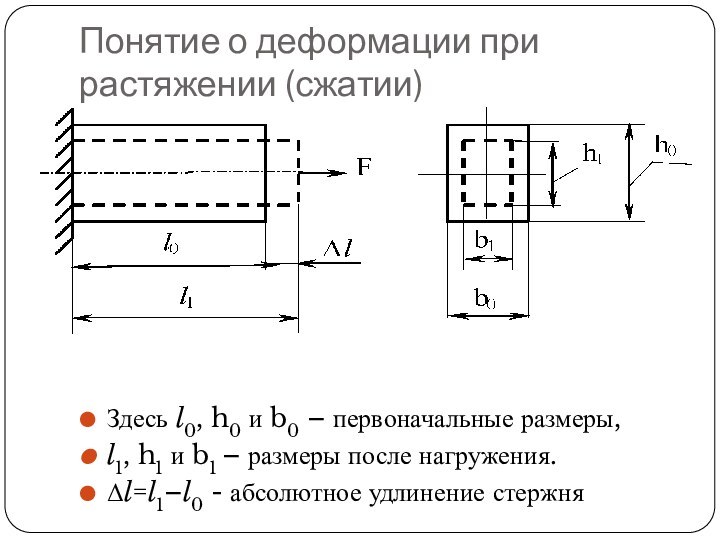
- 11. Понятие о деформации при растяжении (сжатии)Здесь l0,
- 12. Относительное удлинение или продольная деформация ε равнаПоперечные деформации равныДля изотропных материалов
- 13. Экспериментально установлено, что при малых деформацияхгде ν
- 14. Связь между напряжениями и деформациями при растяжении
- 15. Перемещения при растяжении (сжатии) стержняИз (2) можно
- 16. Если стержень можно представить в виде совокупности
- 17. ПримерОпределить изменение длины стального стержня, изображенного на
- 19. Определить перемещение свободного конца призматического стержня, находящегося
- 21. N(x)=–γAx.при x=0, N=0; при x=l, N=–γAl.Перемещение сечения
- 22. Основные механические характеристики конструкционных материаловИспытание на растяжениеИспытания
- 23. При испытании записывается графическая зависимость между растягивающейся силой F и удлинением образца ∆l.Рис. РИ1
- 24. При достижении нагрузки Fmax появляется заметное местное сужение образца (образуется шейка).
- 25. На участке 0 - 1 удлинения растут
- 26. Для удобства изучения механических характеристик диаграмму растяжения
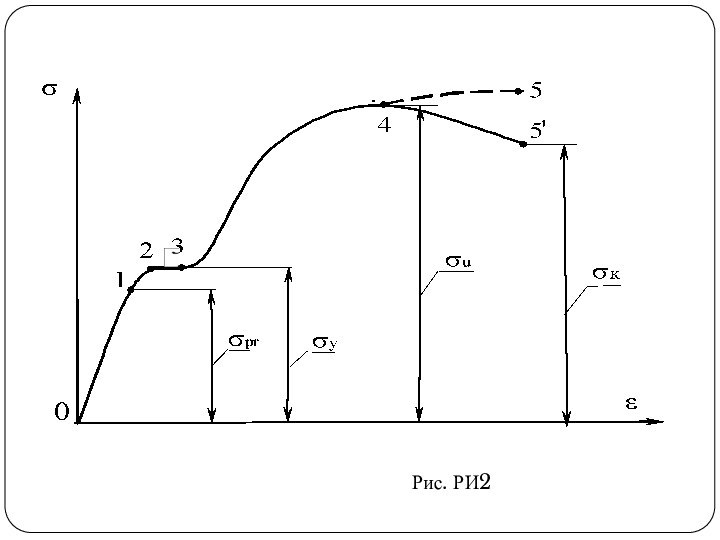
- 27. Рис. РИ2
- 28. характерные точки диаграммы :предел пропорциональности pr=Fpr/A0 (для
- 29. Разрыв образца происходит по наименьшему сечению шейки.
- 30. После разрушения образца разгрузка идет по прямой
- 31. Характеристика пластичности материала Относительное остаточное удлинение при
- 32. Если образец нагружать до напряжения, соответствующего пределу
- 34. Деформация, соответствующая любой точке диаграммы (правее точки
- 35. высокопрочные среднеуглеродистые стали, высокопрочные сплавы не имеют
- 36. Испытание на сжатиеИспытание на сжатие проводятся на цилиндрических образцахДиаграмма напряжений для малоуглеродистой стали
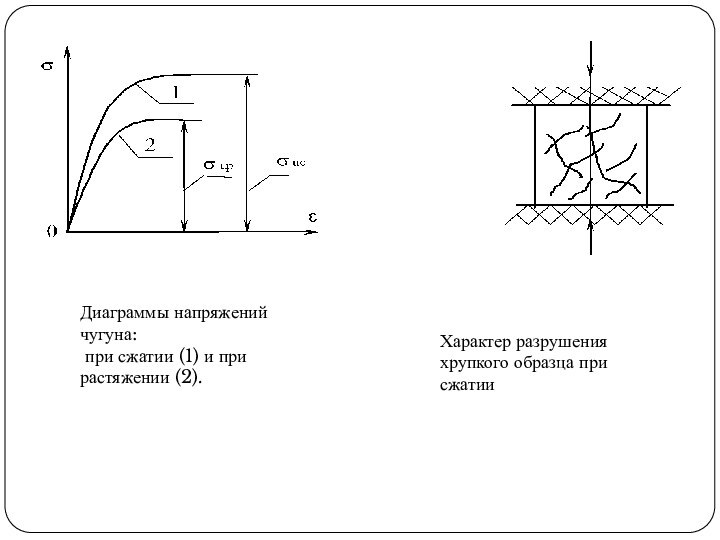
- 37. Диаграммы напряжений чугуна: при сжатии (1) и при растяжении (2).Характер разрушения хрупкого образца при сжатии
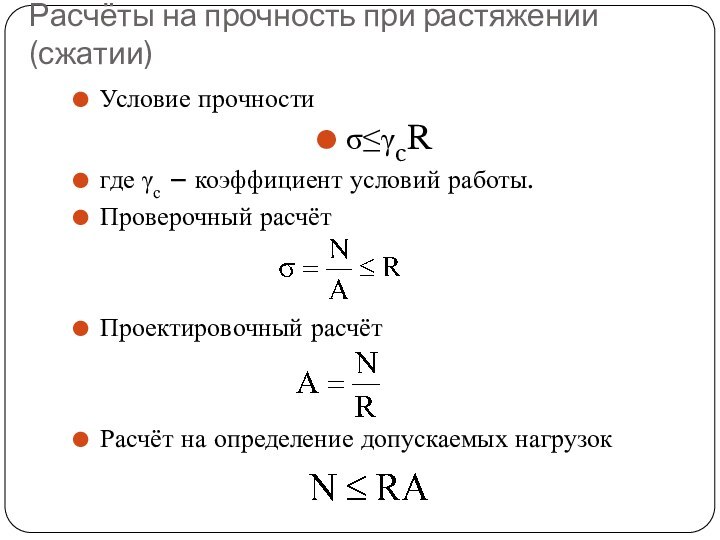
- 38. Расчёты на прочность при растяжении (сжатии)Условие прочностиσ≤γcRгде
- 39. Статически неопределимые стержневые системы при растяжении и
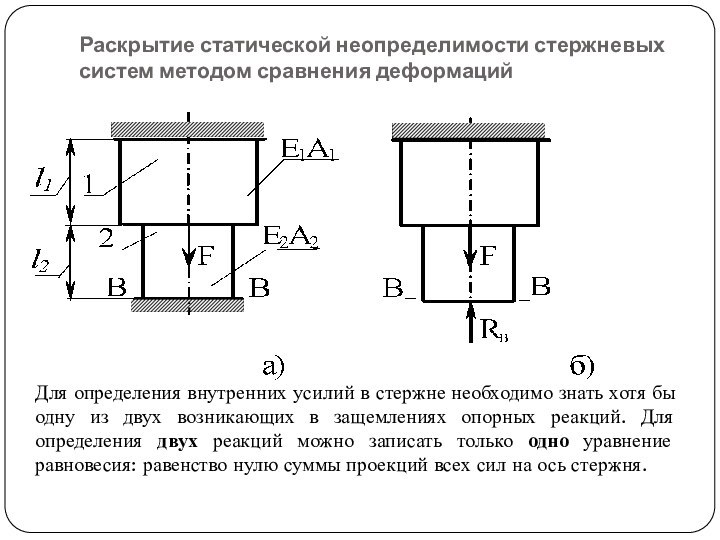
- 40. Раскрытие статической неопределимости стержневых систем методом сравнения
- 41. Запишем дополнительное уравнение - условие совместности деформаций.Отбросим
- 42. Запишем выражение для перемещения сечения В-В и
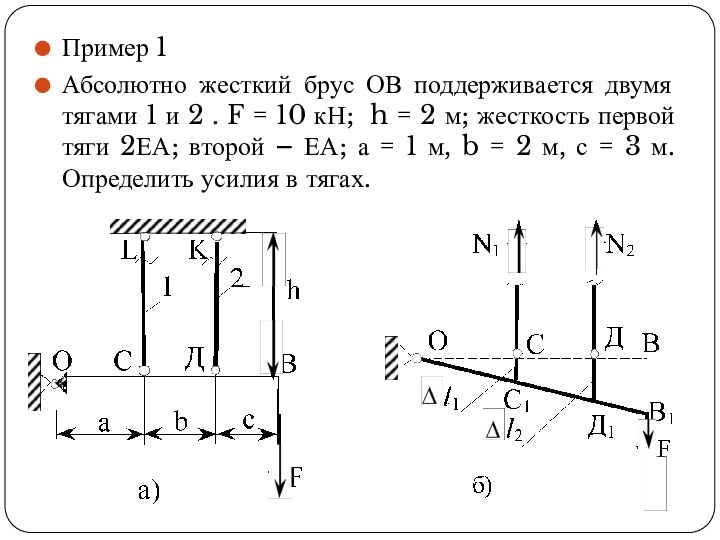
- 43. Пример 1Абсолютно жесткий брус ОВ поддерживается двумя
- 44. При действии внешних сил на рассматриваемую стержневую
- 45. Ввиду малости деформаций можно считать, что точки
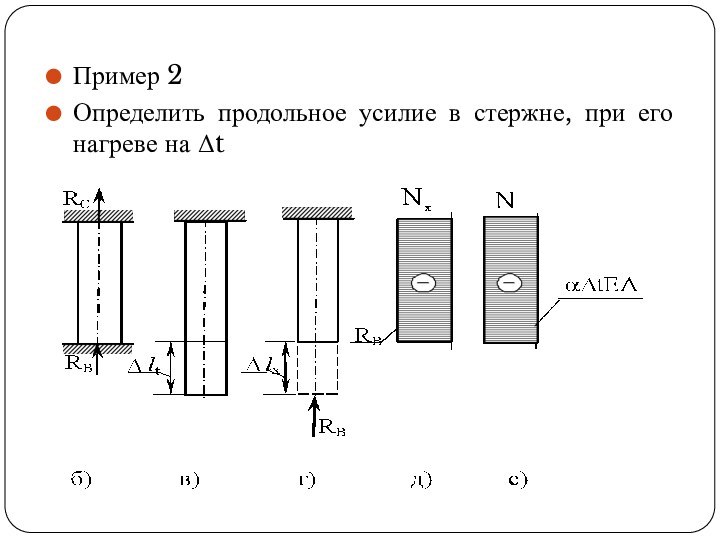
- 46. Пример 2Определить продольное усилие в стержне, при его нагреве на Δt
- 47. Для заданной стержневой системы можно записать одно
- 48. Для восстановления первоначального размера l прикладываем пока
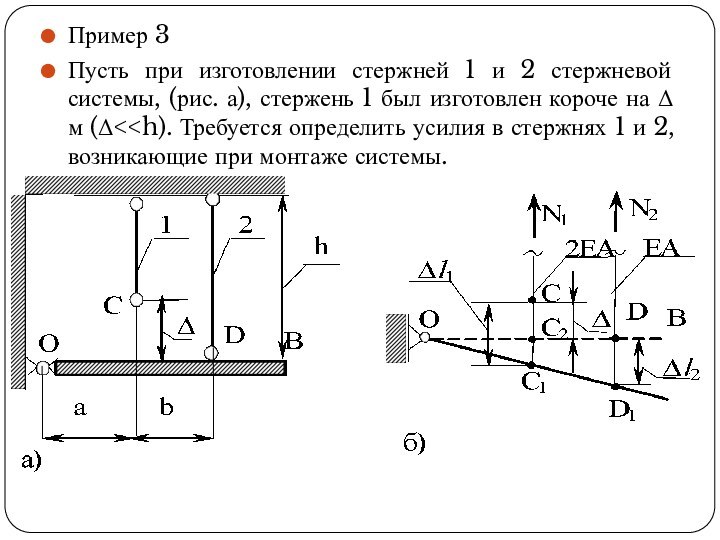
- 49. Пример 3Пусть при изготовлении стержней 1 и
- 50. Скачать презентацию
- 51. Похожие презентации
Определение нормальных усилий и напряжений. Построение эпюрРастяжение (сжатие) стержня это такой вид сопротивления, когда в любом поперечном сечении стержня от действия внешней нагрузки возникает только один вид внутренних усилий - продольное усилие.


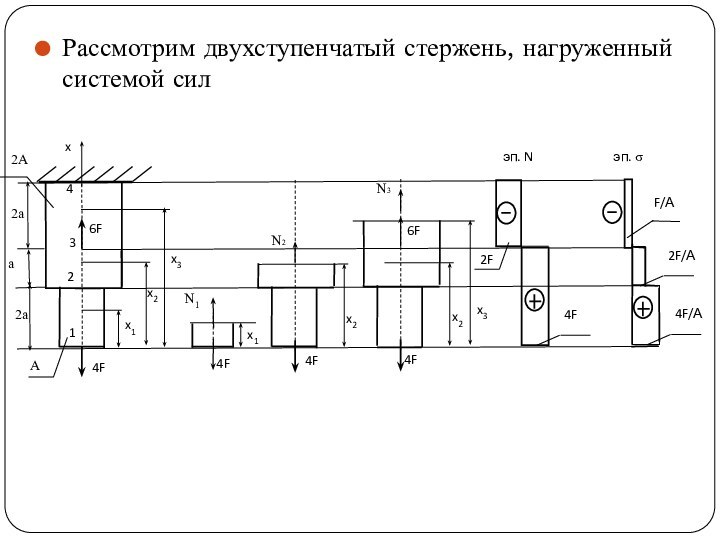






























Слайд 4 Для определения внутренних усилий (продольных сил) применим метод
сечений
Разобьём стержень на участки, границами участков будут места приложения
внешних сил и места изменения сеченийУчасток 1-2 , 0 ≤ x1 ≤ 2a
Рассечем стержень на участке 1-2 сечением x1, отбросим верхнюю часть и рассмотрим равновесие нижней части. Воздействие верхней части на нижнюю заменим силой N1, направив её от сечения, т.е. в положительном направлении. Проектируя все силы, действующие на нижнюю часть, на ось x, и приравнивая сумму проекций нулю, получим
N1–4F=0,
или
N1=4F,
т.е. продольная сила на данном участке – растягивающая.
Напряжение на участке составит
Слайд 5
Участок 2-3 , 2а ≤ x1 ≤ 3a
Рассечем
стержень на участке 2-3 сечением x2, Аналогично участку 1-2
получимN2–4F=0,
или
N2=4F,
Напряжение на участке составит
Слайд 6
Участок 3-4 , 3а ≤ x3 ≤ 5a
Аналогично
получим
N3–4F+6F=0,
или
N3=-2F, Напряжение на участке составит
Слайд 7
Пример
Построить эпюру продольного усилия для стержня, если F=
2 кН, qx = 3 кН/м, l1 = 2
м, l2 = 1 м
Слайд 8
Участок 1-2, 0≤x1 ≤l1
N1=qx1–F
X1=0, N1=-2кН; x1=l1=2м, N1=4кН.
Участок 2-3,
l2 ≤x2 ≤l1+ l2
N2=ql1–F=4кН
Слайд 10
Свойства эпюр N
С учётом выражения (1) можно
заключить
1. Если в сечении к брусу приложена сосредоточенная сила,
то на эпюре N будет «скачок» на величину силы.2. Если на участке приложена осевая распределенная нагрузка постоянной интенсивности, то на эпюре N будет наклонная прямая, причем, тангенс угла наклона прямой к нулевой линии должен быть равен интенсивности нагрузки q.
3. Если на участке отсутствуют внешние нагрузки, то продольная сила будет постоянна.
Слайд 11
Понятие о деформации при растяжении (сжатии)
Здесь l0, h0
и b0 – первоначальные размеры,
l1, h1 и b1
– размеры после нагружения. Δl=l1–l0 - абсолютное удлинение стержня
Слайд 12
Относительное удлинение или продольная деформация ε равна
Поперечные деформации
равны
Для изотропных материалов
Слайд 13
Экспериментально установлено, что при малых деформациях
где ν –
коэффициент Пуассона
Или
Для различных материалов коэффициент Пуассона лежит в пределах
0≤ν≤0,5. Для стали ν=0,25–0,33. Для цветных сплавов ν=0,31–0,42.
Слайд 14
Связь между напряжениями и деформациями при растяжении
(сжатии)
σ=Еε,
где
Е – модуль продольной упругости I рода (или просто
модуль упругости).Модуль упругости Е как и коэффициент Пуассона является механической характеристикой материала и определяется экспериментально. Размерность Е такая же, как и σ, т.е. Н/м2 (Па).
Для стали Е=(2,0 -2,1)∙105МПа,
для медных сплавов Е=(1,0- 1,2)∙105МПа,
для алюминиево-магниевых сплавов Е=(0,7- 0,8)∙105МПа,
для дерева (вдоль волокон) Е=(0,08- 0,12)∙105МПа.
Слайд 15
Перемещения при растяжении (сжатии) стержня
Из (2) можно получить
Для
стержня с переменной по длине продольной силой и изменяемым
поперечным сечением изменение длины равноСлайд 16 Если стержень можно представить в виде совокупности y
участков с длиной li, с постоянным поперечным сечение Аi
и постоянной продольной силой Ni, тогде ΩNi – площадь эпюры N на i участке
Слайд 17
Пример
Определить изменение длины стального стержня, изображенного на рисунке.
Площадь поперечного сечения стержня А=2∙10-3м2, модуль упругости материала Е=2∙1011
Па.Изменение длины всего стержня равно алгебраической сумме изменений длин двух участков - Δl=Δl1+Δl2.
где Nср – среднее значение продольной силы, равное алгебраической полусумме значений N на концах участка
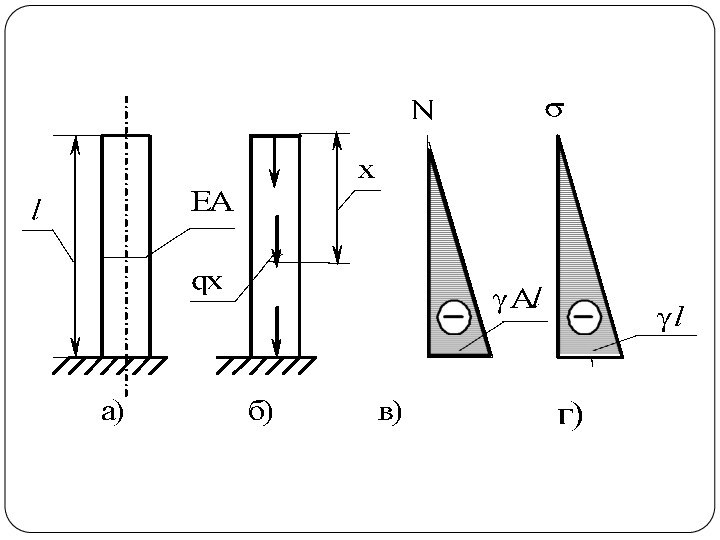
Слайд 19 Определить перемещение свободного конца призматического стержня, находящегося под
действием собственного веса. Длина стержня l, площадь поперечного сечения
А, удельный вес материала γ, модуль упругости материала стержня Е. Построить эпюру нормальных напряжений.Стержень можно рассматривать как находящийся под действием продольной распределенной нагрузки qx, равной весу единицы длины стержня: qx=γ∙A∙1
Слайд 21
N(x)=–γAx.
при x=0, N=0; при x=l, N=–γAl.
Перемещение сечения x
перемещение
свободного конца стержня (х=0)
Нормальные напряжения изменяются по линейному закону:
при x=0, σ=0; при x=l, σ=γl.
Слайд 22
Основные механические характеристики конструкционных материалов
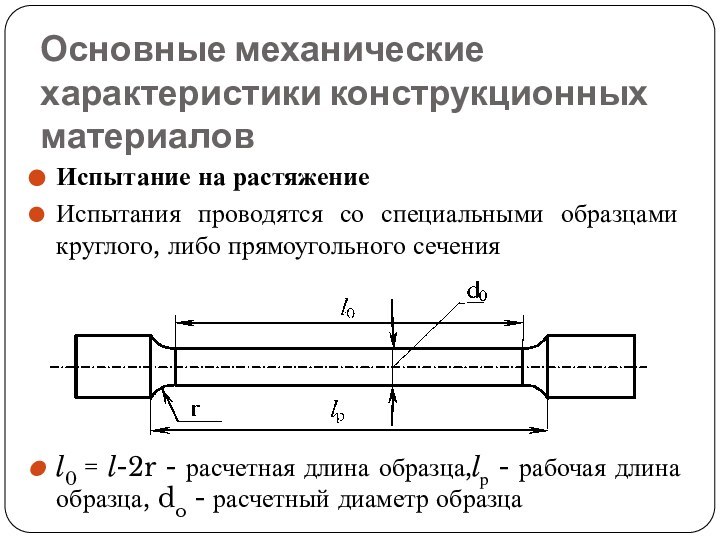
Испытание на растяжение
Испытания проводятся
со специальными образцами круглого, либо прямоугольного сечения
l0 = l-2r
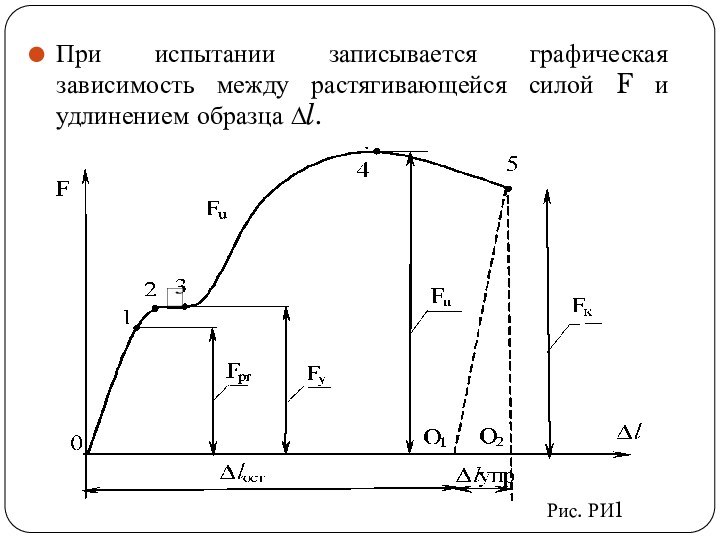
- расчетная длина образца,lр - рабочая длина образца, do - расчетный диаметр образцаСлайд 23 При испытании записывается графическая зависимость между растягивающейся силой
F и удлинением образца ∆l.
Рис. РИ1
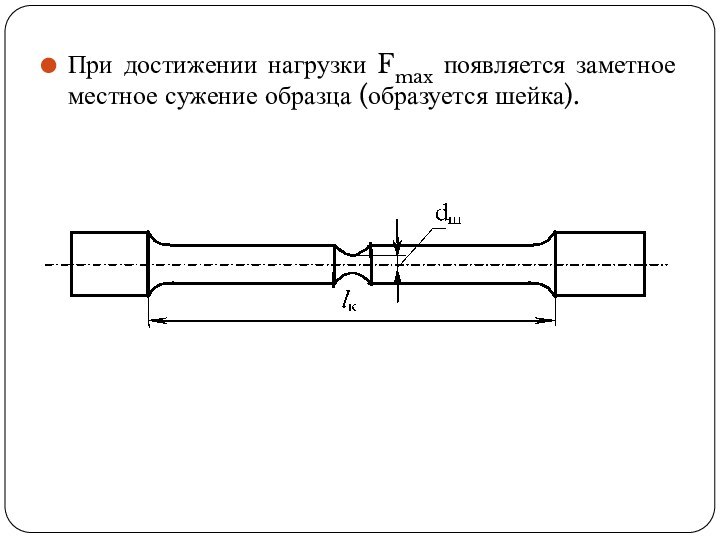
Слайд 24 При достижении нагрузки Fmax появляется заметное местное сужение
образца (образуется шейка).
Слайд 25 На участке 0 - 1 удлинения растут пропорционально
растягивающей силе, согласно закону Гука. Сила, соответствующая точке 1,
обозначается Fpr. При дальнейшем увеличении растягивающей силы прямолинейная зависимость между F и ∆l нарушается. В точке 2 диаграммы наступает явление текучести металла. На диаграмме растяжения получается горизонтальный или близкий к нему участок 2 - 3 (площадка текучести). Для участка 2 - 3 характерен рост деформации без заметного увеличения нагрузки. Нагрузка, соответствующая площадке текучести 2 - 3, обозначается через Fу.Далее, при увеличении силы сверх Fу, происходит упрочнение металла. Участок 3 - 4 называется участком упрочнения, а сила, соответствующая точке 4, обозначается Fu (Fmax)
Участку 4 - 5 соответствует быстрое уменьшение сечения шейки и, как следствие, падает растягивающее усилие. Образец разрушается по наименьшему сечению шейки. Усилие, соответствующее моменту разрыва (точка 5), обозначается Fк.
Слайд 26 Для удобства изучения механических характеристик диаграмму растяжения часто
перестраивают в системе координат σ – ε,
где
- нормальное напряжение впоперечном сечении образца,
относительное удлинение образца
Слайд 28
характерные точки диаграммы :
предел пропорциональности pr=Fpr/A0 (для стали
Ст3 pr210МПа),
предел текучести у=Fу/A0, (для стали Ст3 т240МПа),
предел прочности
(временное сопротивление) u=Fu/A0 (для стали Ст3 u400МПа).Величины u и y называются характеристиками прочности материала.
Слайд 29 Разрыв образца происходит по наименьшему сечению шейки. Поэтому
при определении напряжения разрушения р (точка 5) разрушающую нагрузку
Fк можно относить к площади шейки Аш или к первоначальной площади сечения образца А0. В первом случае диаграмма 0-1-2-3-4-5 называется истинной, во втором случае – условной (0-1-2-3-4-5΄).Слайд 30 После разрушения образца разгрузка идет по прямой линии
5-01, параллельной участку пропорциональности (рисунок РИ1). Отрезок 0-01 -
это остаточное удлинение образца ∆lост, равноеlост=lк-l0.
Отрезок 01-02 - “исчезающая“ при разгрузке упругая составляющая удлинения образца.
Слайд 31
Характеристика пластичности материала Относительное остаточное удлинение при разрыве.
Чем
больше , тем пластичнее материал. Для конструкционных сталей =(16–27)%.
Относительное
сужение сечения шейки после разрываВеличина может достигать для сталей величины 55% и более.
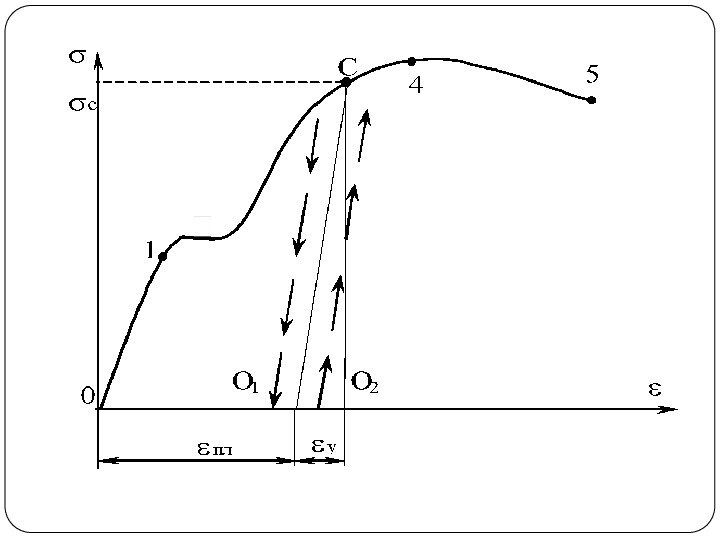
Слайд 32 Если образец нагружать до напряжения, соответствующего пределу пропорциональности,
а потом, остановив машину, начать процесс разгрузки, то деформация
будет уменьшаться по тому же закону, по которому увеличивались при нагружении. При нагрузке образца выше предела пропорциональности (например, до c) деформации при разгрузке будут уменьшаться параллельно участку пропорциональности 0-1 (Рис. РИ.3)Слайд 34 Деформация, соответствующая любой точке диаграммы (правее точки 1)
будет состоять из упругой у и пластической составляющей у
=у+
уПри разгрузке образца упругая деформация исчезает, а остаточная деформация будет равна пластической составляющей. При повторном нагружении диаграмма деформирования будет сначала совпадать с прямой О-С, а затем с кривой С - 4 - 5 . Таким образом, при повторном нагружении образца повышается предел пропорциональности .
Явление повышения предела пропорциональности при предварительном нагружении выше предела текучести называется наклепом (упрочнением). Наклеп используется в технике для повышения эксплуатационной надежности деталей и для уменьшения деформации в процессе эксплуатации
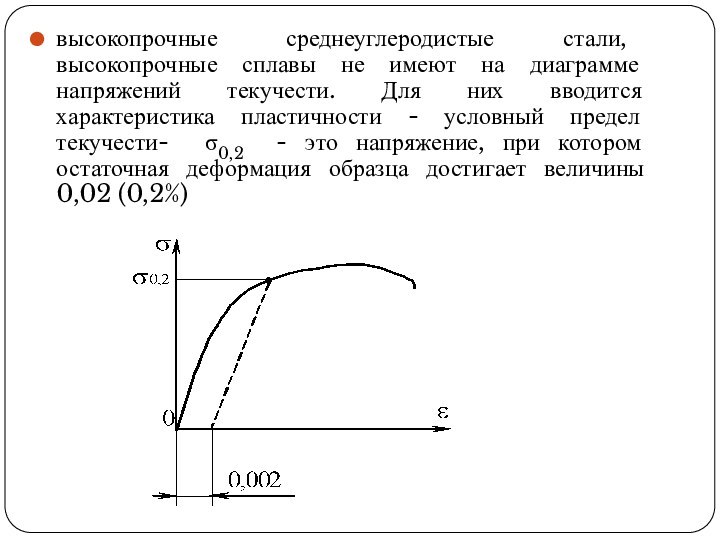
Слайд 35 высокопрочные среднеуглеродистые стали, высокопрочные сплавы не имеют на
диаграмме напряжений текучести. Для них вводится характеристика пластичности -
условный предел текучести- 0,2 - это напряжение, при котором остаточная деформация образца достигает величины 0,02 (0,2%)
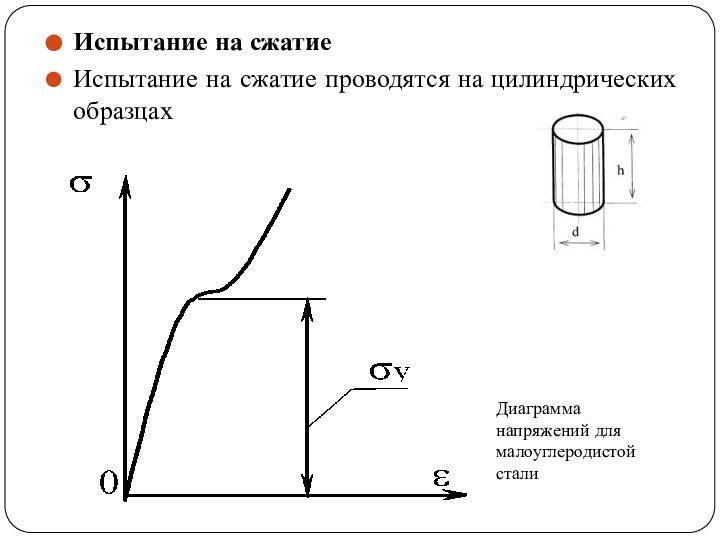
Слайд 36
Испытание на сжатие
Испытание на сжатие проводятся на цилиндрических
образцах
Диаграмма напряжений для малоуглеродистой стали
Слайд 37
Диаграммы напряжений чугуна:
при сжатии (1) и при
растяжении (2).
Характер разрушения хрупкого образца при сжатии
Слайд 38
Расчёты на прочность при растяжении (сжатии)
Условие прочности
σ≤γcR
где γс
– коэффициент условий работы.
Проверочный расчёт
Проектировочный расчёт
Расчёт на определение допускаемых
нагрузок
Слайд 39
Статически неопределимые стержневые системы при растяжении и сжатии
Стержневые
системы, внутренние усилия в которых не могут быть определены
только из условий равновесия стержневой системы как твердого тела., называют статически неопределимыми.В статически неопределимых стержневых системах, в отличие от статически определимых стержневых систем, внутренние усилия возникают не только под действием внешних усилий, но и при изменении температуры всей системы, либо отдельных стержней, а так же при осадке (смещении) опор и наличии зазоров в соединяемых узлах (монтажные усилия).
Для определения внутренних усилий в статических неопределимых стержневых системах, наряду с уравнениями равновесия стержневой системы как твердого тела, составляются дополнительные уравнения – условия совместности деформаций.
Слайд 40
Раскрытие статической неопределимости стержневых систем методом сравнения деформаций
Для
определения внутренних усилий в стержне необходимо знать хотя бы
одну из двух возникающих в защемлениях опорных реакций. Для определения двух реакций можно записать только одно уравнение равновесия: равенство нулю суммы проекций всех сил на ось стержня.
Слайд 41
Запишем дополнительное уравнение - условие совместности деформаций.
Отбросим одно
из защемлений, например, нижнее В-В, заменив его действие на
стержень неизвестной силой RВ. В исходной системе сечение В-В не имеет возможности смещаться. Поэтому перемещение торца В-В при совместном действии внешних сил (в нашей задаче – сила F) и неизвестной силы RВ должно быть равно нулю, а неизвестная сила будет равна опорной реакции.Слайд 42 Запишем выражение для перемещения сечения В-В и приравняем
его нулю
Используя найденное значение RB, легко определить продольные силы
в сечениях стержня по методу сечений, как для статически определимой задачи.Данный метод раскрытия статической неопределимости, называется методом сравнения деформаций, используется для решения один раз статически неопределимых систем.
Слайд 43
Пример 1
Абсолютно жесткий брус ОВ поддерживается двумя тягами
1 и 2 . F = 10 кН; h
= 2 м; жесткость первой тяги 2ΕА; второй – ΕА; а = 1 м, b = 2 м, с = 3 м. Определить усилия в тягах.Слайд 44 При действии внешних сил на рассматриваемую стержневую систему
возникает четыре опорные реакции: две в шарнире O и
по одной в шарнирах L и К. Для определения опорных реакций имеем три независимых уравнения статики, то есть система один раз статически неопределима.При нагружении жесткий брус ОB будет поворачиваться по часовой стрелке вокруг точки O и займет положение OВ1. Стержни 1 и 2 будут растягиваться. Отсечем тяги от верхних опор
Составим уравнение равновесия:
ΣМo = 0; N1 ∙ a + N2(a + b) – F(a + b + c) = 0. (1)
Из этого уравнения нельзя определить два неизвестных внутренних усилия N1 и N2.
Составим дополнительное уравнение, (уравнение совместимости деформаций).
Слайд 45 Ввиду малости деформаций можно считать, что точки C
и D при нагружении будут перемещаться перпендикулярно линии OВ,
а удлинения стержней будут равны: Δl1 = СС1 и Δl2 = DD1Из подобия треугольников OCC1 и ODD1 следует:
Или
Решая совместно (1) и (2) получаем усилия в стержнях N1 = 10,9 кН , N2 = 16,35 кН.
Слайд 47 Для заданной стержневой системы можно записать одно уравнение
статики – равенство нулю проекций всех сил на ось
стержняRC +RB = 0 .
Из одного уравнения нельзя определить две опорные реакции.
Отбросим нижнее защемление (рис. в). Стержень стал статически определимым и удлинился при нагреве на
Слайд 48 Для восстановления первоначального размера l прикладываем пока неизвестную
силу RB (рис. г)
Изменение длины от силы RB
с учетом эпюры Nx (рис. д) равноДолжно выполняться условие совместности деформаций:
Δlt + Δlx = 0 ,
Или





























![Согласные звуки [б], [б’], буквы Б, б](/img/tmb/13/1206915/7e8335a7d65c29f66fd521fec5d176a4-210x.jpg)