- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Раздел: “Общие сведения по инженерной графике”
Содержание
- 2. Цели занятия:Формирование знаний, умений и навыков по геометрическим построениям и выполнению сопряжений.
- 3. Проведение перпендикуляров из заданной точки к произвольной прямойНа прямой a откладываем две произвольные точки A, B.
- 4. Проведение перпендикуляров из заданной точки к произвольной
- 5. Проведение перпендикуляров из заданной точки к произвольной
- 6. Деление отрезка на 2,4,8 и т.д. частейИз
- 7. Деление отрезка на 2,4,8 и т.д. частейПрямая,
- 8. Деление отрезка на n-ое количество данных частейПод любым острым углом к отрезку AB проводим вспомогательную прямую.
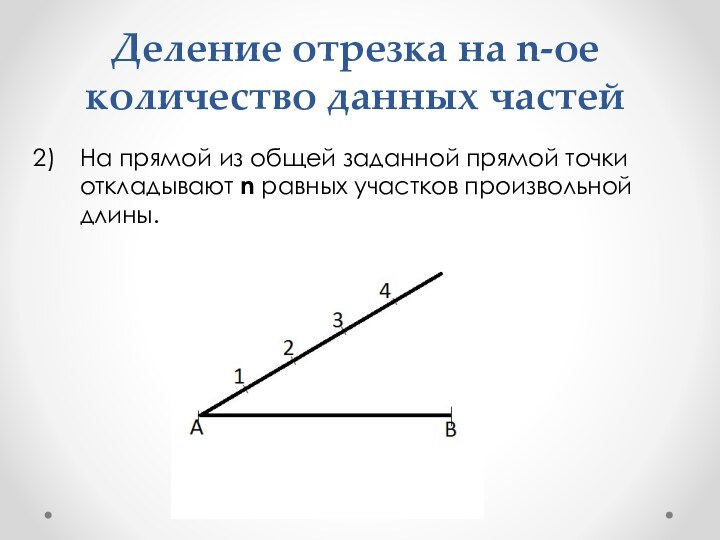
- 9. Деление отрезка на n-ое количество данных частейНа
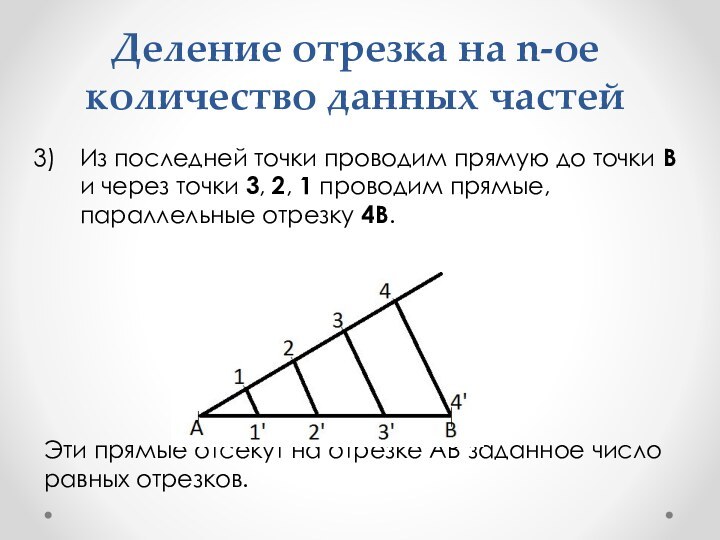
- 10. Деление отрезка на n-ое количество данных частейИз
- 11. Деление угла пополамИз вершины А данного угла,
- 12. Деление угла пополамИз точки B, как из центра тем же радиусом R проводим дугу.
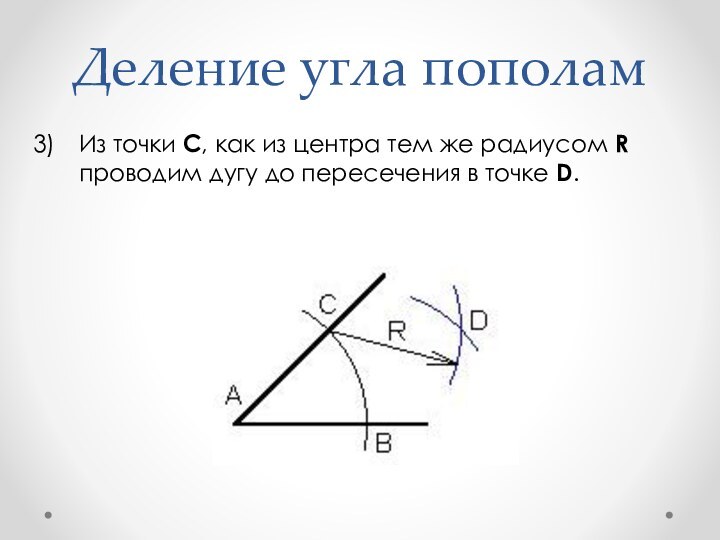
- 13. Деление угла пополамИз точки С, как из
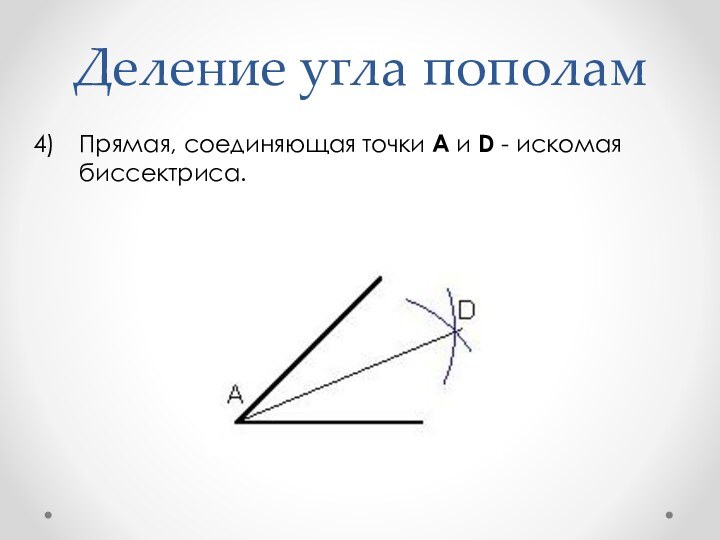
- 14. Деление угла пополамПрямая, соединяющая точки A и D - искомая биссектриса.
- 15. Деление прямого угла на 3 равные частиИз
- 16. Деление прямого угла на 3 равные частиИз
- 17. Деление прямого угла на 3 равные частиИз
- 18. Деление прямого угла на 3 равные частиИз
- 19. Деление окружности на 3, 6, 12 равных частейВ окружности радиуса R следует провести вертикальный диаметр.
- 20. Деление окружности на 3, 6, 12 равных
- 21. Деление окружности на 3, 6, 12 равных
- 22. Деление окружности на 3, 6, 12 равных
- 23. Деление окружности на 7 равных частейСторона правильного
- 24. Деление окружности на 7 равных частейОснование правильного
- 25. Деление окружности на 7 равных частейРадиусом дуги
- 26. Деление окружности на 7 равных частейИз точки
- 27. Деление окружности на 4, 8 равных частейПроводим в окружности вертикальный и горизонтальный диаметры
- 28. Деление окружности на 4, 8 равных частейИз
- 29. Деление окружности на 4, 8 равных частейПроводим
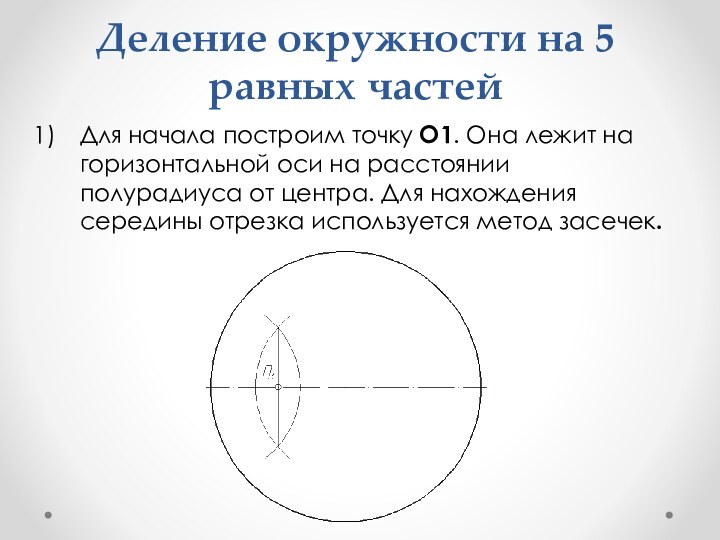
- 30. Деление окружности на 5 равных частейДля начала
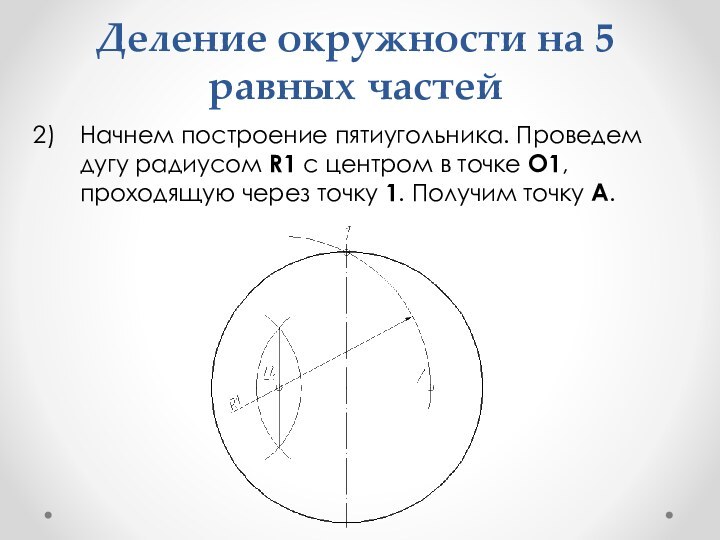
- 31. Деление окружности на 5 равных частейНачнем построение пятиугольника.
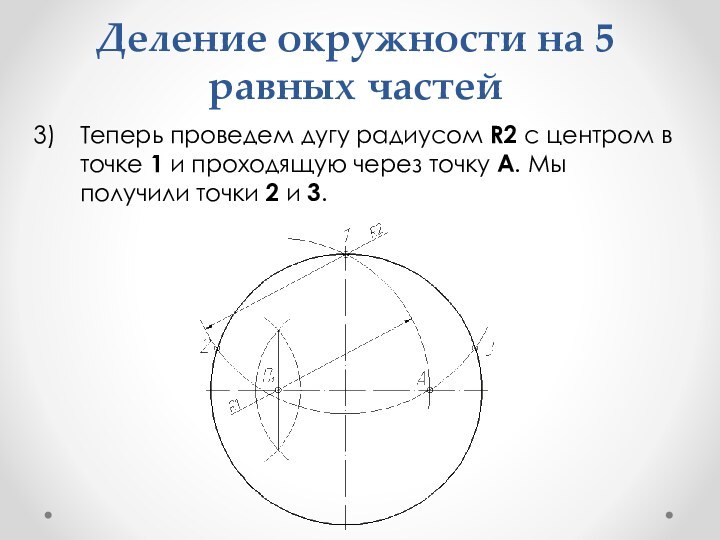
- 32. Деление окружности на 5 равных частейТеперь проведем
- 33. Деление окружности на 5 равных частейИз точек
- 34. Деление окружности на 5 равных частейДля наглядности соединим полученные точки между собой - получим правильный пятиугольник.
- 35. СопряженияСопряжение – плавный переход одной линии в
- 36. Внешним называется сопряжение, в котором сопрягающая дуга
- 37. Сопряжение двух прямых.Возьмем раствор циркуля, равный заданному
- 38. Сопряжение двух прямых.К ним проведем две касательные
- 39. Сопряжение двух прямых.Поставив ножку циркуля в центр
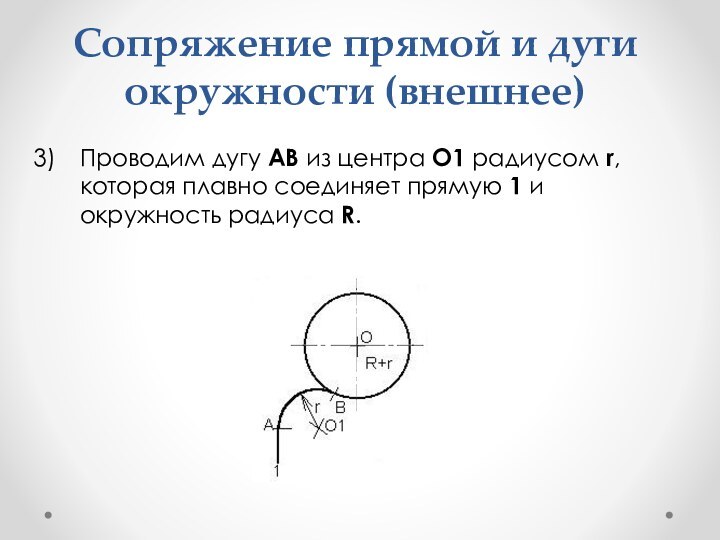
- 40. Сопряжение прямой и дуги окружности (внешнее)Проведем прямую
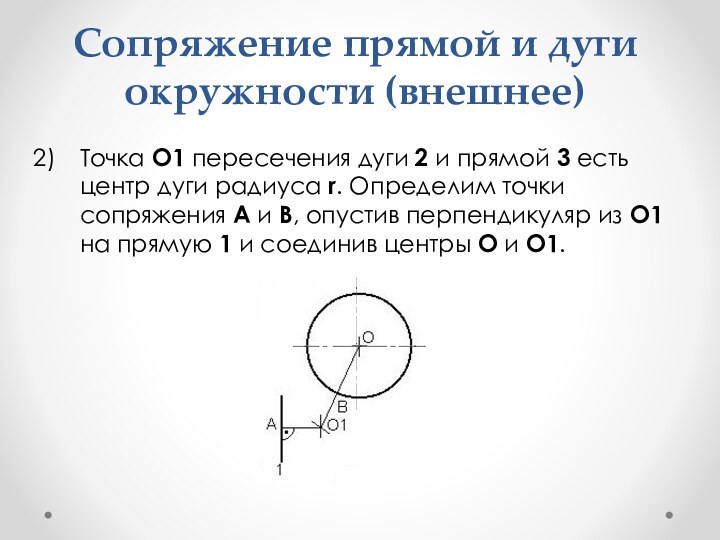
- 41. Сопряжение прямой и дуги окружности (внешнее)Точка О1
- 42. Сопряжение прямой и дуги окружности (внешнее)Проводим дугу
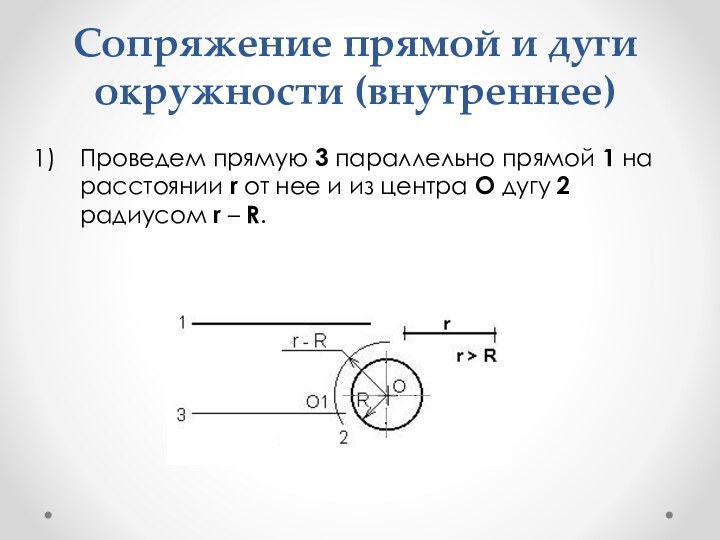
- 43. Сопряжение прямой и дуги окружности (внутреннее)Проведем прямую
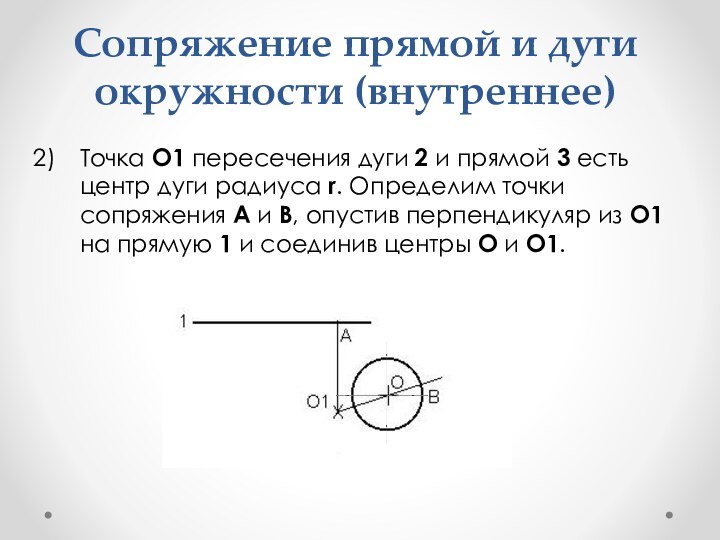
- 44. Сопряжение прямой и дуги окружности (внутреннее)Точка О1
- 45. Сопряжение прямой и дуги окружности (внутреннее)Проводим дугу
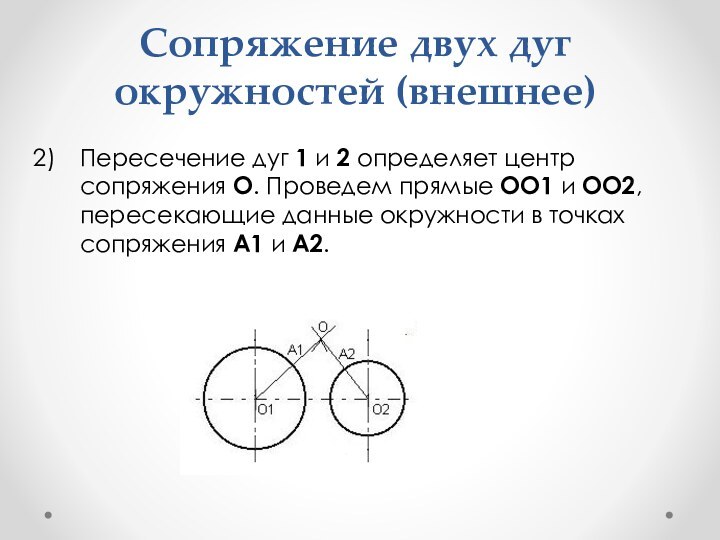
- 46. Сопряжение двух дуг окружностей (внешнее)Проведем радиусами R1+R
- 47. Сопряжение двух дуг окружностей (внешнее)Пересечение дуг 1
- 48. Сопряжение двух дуг окружностей (внешнее)Из центра О
- 49. Сопряжение двух дуг окружностей (внутреннее)Сопрягающая дуга касается
- 50. Сопряжение двух дуг окружностей (комбинированное)Одна из заданных
- 51. Скачать презентацию
- 52. Похожие презентации
Цели занятия:Формирование знаний, умений и навыков по геометрическим построениям и выполнению сопряжений.
Слайд 2
Цели занятия:
Формирование знаний, умений и навыков по геометрическим
построениям и выполнению сопряжений.
Слайд 3
Проведение перпендикуляров из заданной точки к произвольной прямой
На
прямой a откладываем две произвольные точки A, B.
Слайд 4
Проведение перпендикуляров из заданной точки к произвольной прямой
Из
точек A, B проводим дуги произвольного радиуса R, которые
пересекутся в точках C, D.
Слайд 5
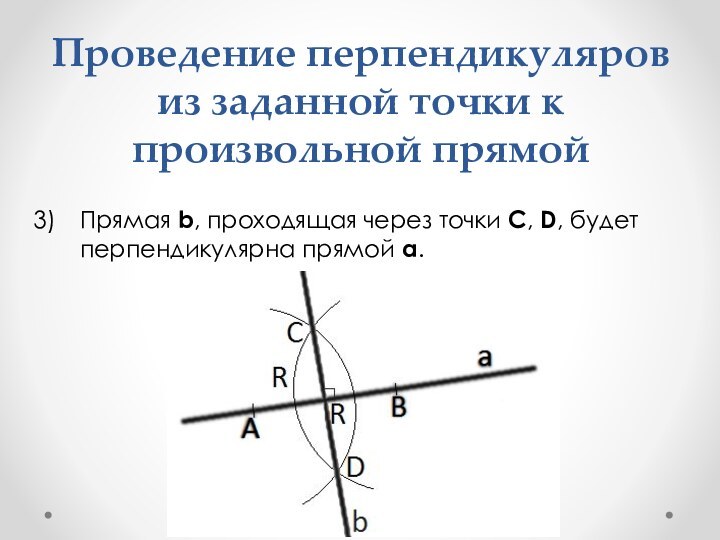
Проведение перпендикуляров из заданной точки к произвольной прямой
Прямая
b, проходящая через точки C, D, будет перпендикулярна прямой
a.
Слайд 6
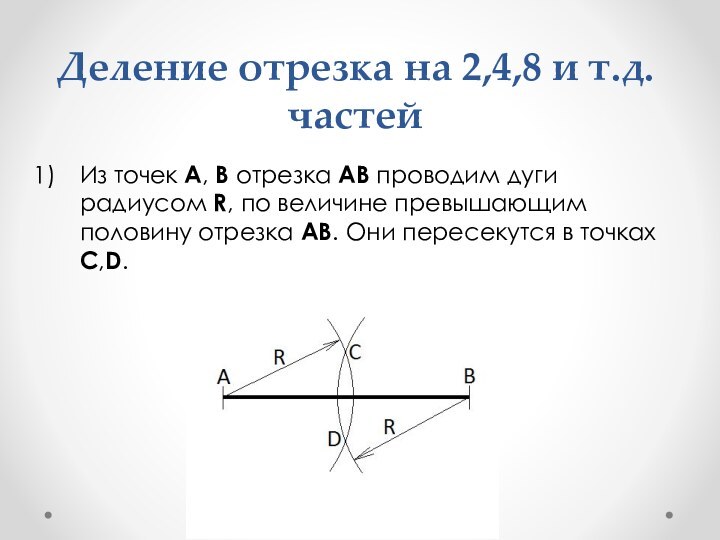
Деление отрезка на 2,4,8 и т.д. частей
Из точек
A, B отрезка AB проводим дуги радиусом R, по
величине превышающим половину отрезка AB. Они пересекутся в точках C,D.
Слайд 7
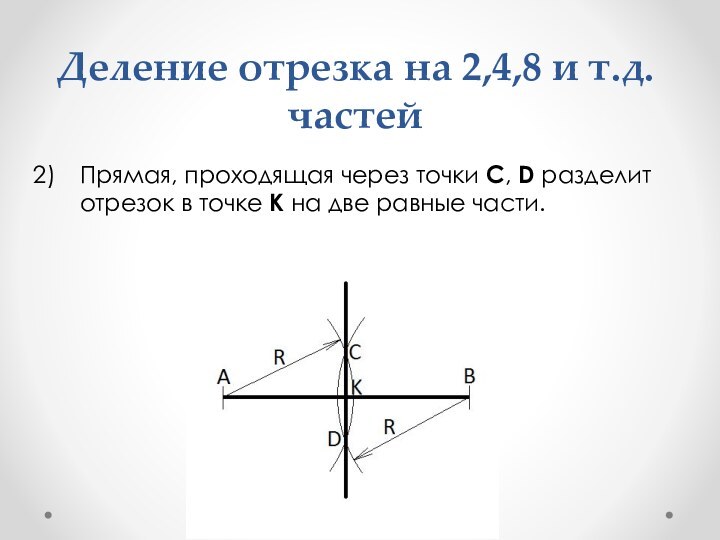
Деление отрезка на 2,4,8 и т.д. частей
Прямая, проходящая
через точки C, D разделит отрезок в точке K
на две равные части.
Слайд 8
Деление отрезка на n-ое количество данных частей
Под любым
острым углом к отрезку AB проводим вспомогательную прямую.
Слайд 9
Деление отрезка на n-ое количество данных частей
На прямой
из общей заданной прямой точки откладывают n равных участков
произвольной длины.
Слайд 10
Деление отрезка на n-ое количество данных частей
Из последней
точки проводим прямую до точки B и через точки
3, 2, 1 проводим прямые, параллельные отрезку 4B.Эти прямые отсекут на отрезке AB заданное число равных отрезков.
Слайд 11
Деление угла пополам
Из вершины А данного угла, как
из центра проводим дугу произвольного радиуса R, которая пересечет
стороны угла в точках C,B.
Слайд 13
Деление угла пополам
Из точки С, как из центра
тем же радиусом R проводим дугу до пересечения в
точке D.
Слайд 15
Деление прямого угла на 3 равные части
Из вершины
прямого угла А, как из центра, следует провести дугу
BC, произвольного радиуса R.
Слайд 16
Деление прямого угла на 3 равные части
Из точки
B, как из центра, проводим дугу, тем же радиусом
R, до пересечения с дугой BC в точке D.
Слайд 17
Деление прямого угла на 3 равные части
Из точки
C, как из центра, проводим дугу, тем же радиусом
R, до пересечения с дугой BC в точке E.
Слайд 18
Деление прямого угла на 3 равные части
Из точки
А проводим линии AD и AE, которые и делят
прямой угол BAC на три равных между собой угла BAE, EAD и DAC.
Слайд 19
Деление окружности на 3, 6, 12 равных частей
В
окружности радиуса R следует провести вертикальный диаметр.
Слайд 20
Деление окружности на 3, 6, 12 равных частей
Из
нижней точки пересечения диаметра с окружностью, как из центра
следует провести дугу радиусом R, равным радиусу окружности.
Слайд 21
Деление окружности на 3, 6, 12 равных частей
Аналогично,
из верхней точки пересечения диаметра с окружностью следует провести
дугу радиусом R. Окружность поделена на 6 частей.
Слайд 22
Деление окружности на 3, 6, 12 равных частей
Выполнив
аналогичные действия с горизонтальным диаметром, можно поделить окружность на
12 равных частей.
Слайд 23
Деление окружности на 7 равных частей
Сторона правильного семиугольника
приближенно равна 1/2 стороны правильного треугольника. Поэтому сначала следует
построить основание правильного треугольника.
Слайд 24
Деление окружности на 7 равных частей
Основание правильного треугольника
AB делится пополам в точке С вертикальным диаметром окружности.
Длинна отрезка z = AC является длиной стороны правильного семиугольника.
Слайд 25
Деление окружности на 7 равных частей
Радиусом дуги равным
z следует сделать на окружности засечки, как показано на
рисунке.
Слайд 26
Деление окружности на 7 равных частей
Из точки D,
последовательно следует соединить все точки пересечения дуг с окружностью.
В итоге получаем правильный семиугольник.
Слайд 27
Деление окружности на 4, 8 равных частей
Проводим в
окружности вертикальный и горизонтальный диаметры
Слайд 28
Деление окружности на 4, 8 равных частей
Из точек
пересечения диаметров с окружностью строим дуги с радиусом R,
равным радиусу окружности.
Слайд 29
Деление окружности на 4, 8 равных частей
Проводим прямые
через точки пересечения дуг. Точки, в которых прямые пересекут
окружность, поделят её на 4 части.
Слайд 30
Деление окружности на 5 равных частей
Для начала построим
точку О1. Она лежит на горизонтальной оси на расстоянии
полурадиуса от центра. Для нахождения середины отрезка используется метод засечек.
Слайд 31
Деление окружности на 5 равных частей
Начнем построение пятиугольника. Проведем
дугу радиусом R1 с центром в точке О1, проходящую
через точку 1. Получим точку А.
Слайд 32
Деление окружности на 5 равных частей
Теперь проведем дугу
радиусом R2 с центром в точке 1 и проходящую
через точку А. Мы получили точки 2 и 3.
Слайд 33
Деление окружности на 5 равных частей
Из точек 2
и 3 таким же радиусом R2 сделаем еще две
засечки на окружности - точки 4 и 5. Таким образом, мы получил пять точек, делящих окружность на 5 равных частей
Слайд 34
Деление окружности на 5 равных частей
Для наглядности соединим
полученные точки между собой - получим правильный пятиугольник.
Слайд 35
Сопряжения
Сопряжение – плавный переход одной линии в другую
линию или дугу окружности.
Точка сопряжения – точка, в которой
одна линия переходит в другую.Слайд 36 Внешним называется сопряжение, в котором сопрягающая дуга касается
заданных окружностей внешней стороной
Внутренним называется сопряжение, в котором сопрягающая
дуга касается заданных окружностей внутренней стороной.
Слайд 37
Сопряжение двух прямых.
Возьмем раствор циркуля, равный заданному радиусу
R=AB. Поочередно поставим ножку циркуля в две произвольные точки
на каждой из прямых. Проведем по дуге из каждой точки.
Слайд 38
Сопряжение двух прямых.
К ним проведем две касательные до
пересечения в точке О — центре сопряжения. Из центра
сопряжения опустим перпендикуляры к прямым. Полученные точки а и b будут точками сопряжения.
Слайд 39
Сопряжение двух прямых.
Поставив ножку циркуля в центр сопряжения
(О), раствором циркуля, равным заданному радиусу сопряжения (R=AB), проведем
дугу сопряжения.
Слайд 40
Сопряжение прямой и дуги окружности (внешнее)
Проведем прямую 3
параллельно прямой 1 на расстоянии r от нее и
из центра О дугу 2 радиусом R+r.
Слайд 41
Сопряжение прямой и дуги окружности (внешнее)
Точка О1 пересечения
дуги 2 и прямой 3 есть центр дуги радиуса
r. Определим точки сопряжения А и В, опустив перпендикуляр из О1 на прямую 1 и соединив центры О и О1.
Слайд 42
Сопряжение прямой и дуги окружности (внешнее)
Проводим дугу АВ
из центра О1 радиусом r, которая плавно соединяет прямую
1 и окружность радиуса R.
Слайд 43
Сопряжение прямой и дуги окружности (внутреннее)
Проведем прямую 3
параллельно прямой 1 на расстоянии r от нее и
из центра О дугу 2 радиусом r – R.
Слайд 44
Сопряжение прямой и дуги окружности (внутреннее)
Точка О1 пересечения
дуги 2 и прямой 3 есть центр дуги радиуса
r. Определим точки сопряжения А и В, опустив перпендикуляр из О1 на прямую 1 и соединив центры О и О1.
Слайд 45
Сопряжение прямой и дуги окружности (внутреннее)
Проводим дугу АВ
из центра О1 радиусом r, которая плавно соединяет прямую
1 и окружность радиуса R.
Слайд 46
Сопряжение двух дуг окружностей (внешнее)
Проведем радиусами R1+R и
R2+R две дуги 1 и 2, концентрические данным окружностям.
Слайд 47
Сопряжение двух дуг окружностей (внешнее)
Пересечение дуг 1 и
2 определяет центр сопряжения О. Проведем прямые ОО1 и
ОО2, пересекающие данные окружности в точках сопряжения А1 и А2.
Слайд 48
Сопряжение двух дуг окружностей (внешнее)
Из центра О радиусом
ОА1 проведем дугу А1А2, которая плавно соединяет данные окружности.
Слайд 49
Сопряжение двух дуг окружностей (внутреннее)
Сопрягающая дуга касается заданных
окружностей внутренней стороной. Центр О сопрягающей дуги определяется пересечением дуг вспомогательных
окружностей, радиусы которых равны разностям (R-R1) и (R-R2).
Слайд 50
Сопряжение двух дуг окружностей (комбинированное)
Одна из заданных окружностей
