- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Различия между статистической и клинической значимостью
Содержание
- 3. Типы данных
- 4. Производные (вторичные) данныеПроцентыПропорции или отношенияМетки, оценкиИнтенсивность
- 5. Основные принципы и методы статистического анализа
- 6. Цель биомедицинских исследований заключается в выявлении некоторых
- 7. Выявление закономерностей на выборке производится обычно путем решения задач, для решения которых существуют соответствующие статистические методы
- 8. Выявление закономерностей на выборке производится обычно путем решения задач, для решения которых существуют соответствующие статистические методы
- 9. Статистический анализ основан на допущении: то,
- 10. Распределение признакаРаспределением признака в выборке называется совокупность
- 11. Эмпирическое распределение признака
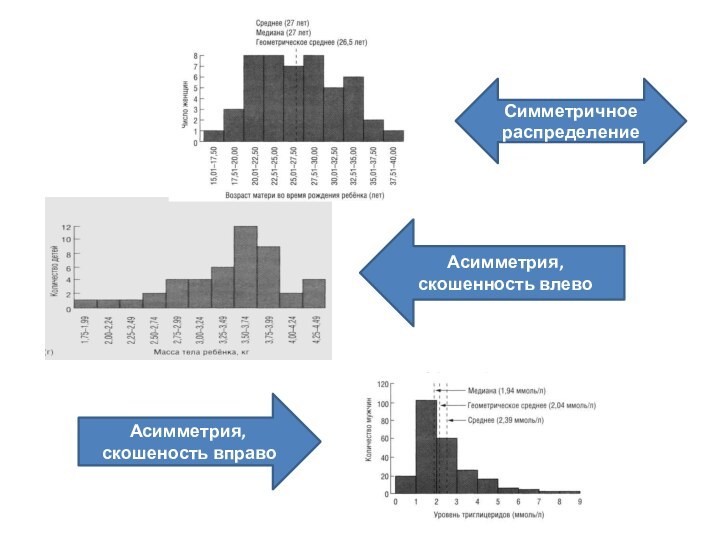
- 12. Асимметрия, скошенность влевоАсимметрия, скошеность вправоСимметричное распределение
- 13. Теоретическое распределениеТеоретическое распределение можно описать с помощью
- 14. Основные типы и виды распределений
- 15. Важно!Уметь отличать нормально распределенные данные от других
- 16. Важно! Если при расчетах среднего и стандартного
- 17. Нормальное (гауссовское) распределениеФункция плотности распределения вероятности:Определяется двумя
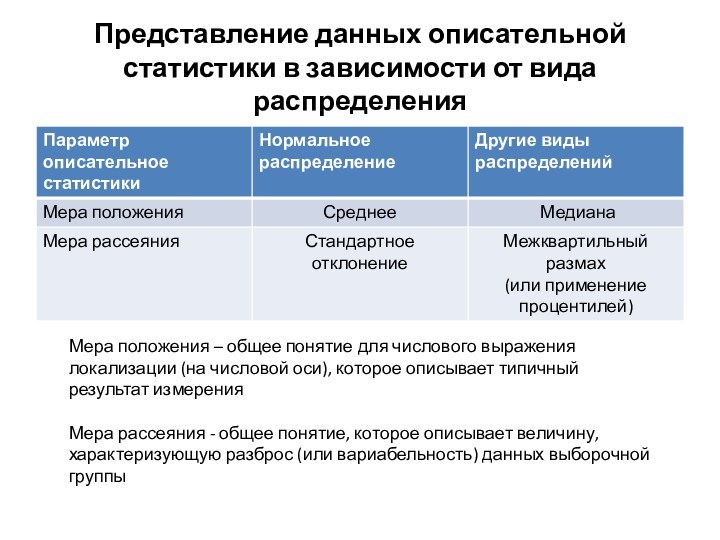
- 18. Представление данных описательной статистики в зависимости от
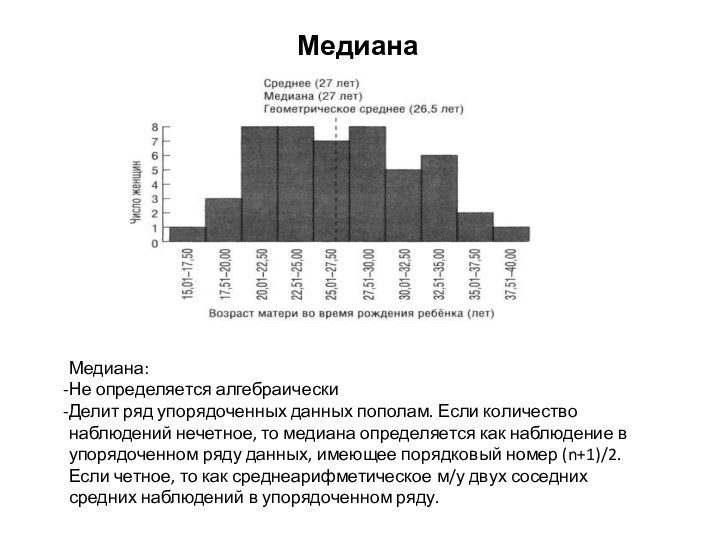
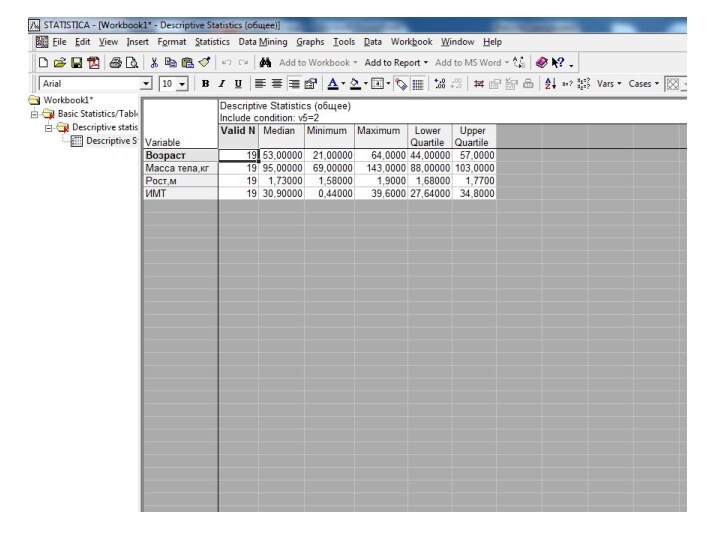
- 19. МедианаМедиана:Не определяется алгебраическиДелит ряд упорядоченных данных пополам.
- 20. ПроцентилиЧто такое процентили?Расположим наши данные упорядоченоВеличина Х,
- 21. Общее свойство медианы и перцентилейНе искажаются ассиметрией распределенияНе подвержены влиянию выбросовНе зависят отразмера выборки
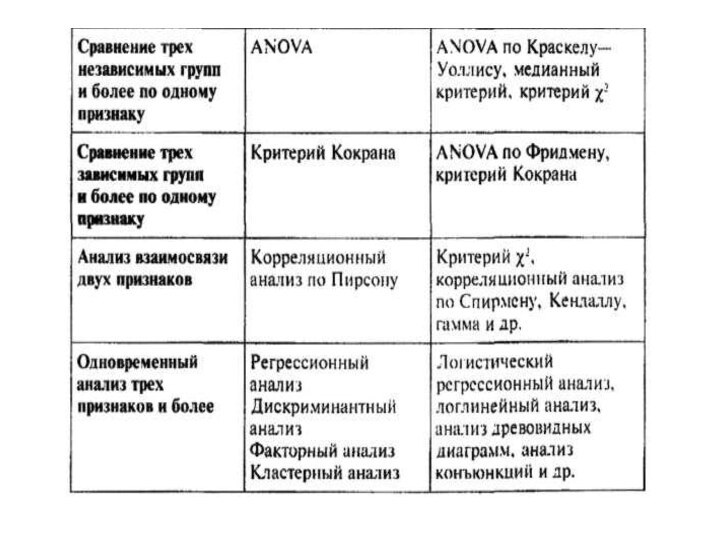
- 30. Классификация методов статистического анализа
- 39. От свойств выборки к свойствам популяцииПреимущество доверительных
- 40. Доверительный интервалдиапазон значений признака, рассчитанный для какого-либо параметра по выборке с определенной (доверительной) вероятностью
- 41. Предпочтительность обоснования использования доверительного интервала в медицинских
- 42. Представление данных исследованияПриводите числовые данные с разумной степенью точностиСредний возраст 22,456 лет 22,5р=0,00002 р
- 43. Представление данных исследованияУказывая число процентов, всегда добавляйте
- 44. Представление данных исследованияЕсли объем выборки меньше 100,
- 45. Представление категориальных данных исследованияУточняйте знаменатели в отношениях,
- 46. Представление категориальных данных исследованияИногда категориальные данные усредняют,
- 47. Представление непрерывных данных исследованияОбразец презентацииЧисленность титров антител
- 48. Скачать презентацию
- 49. Похожие презентации
Типы данных







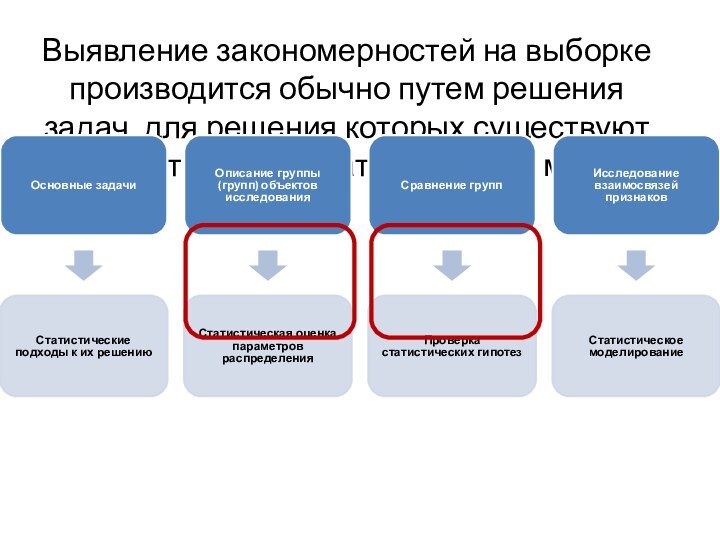










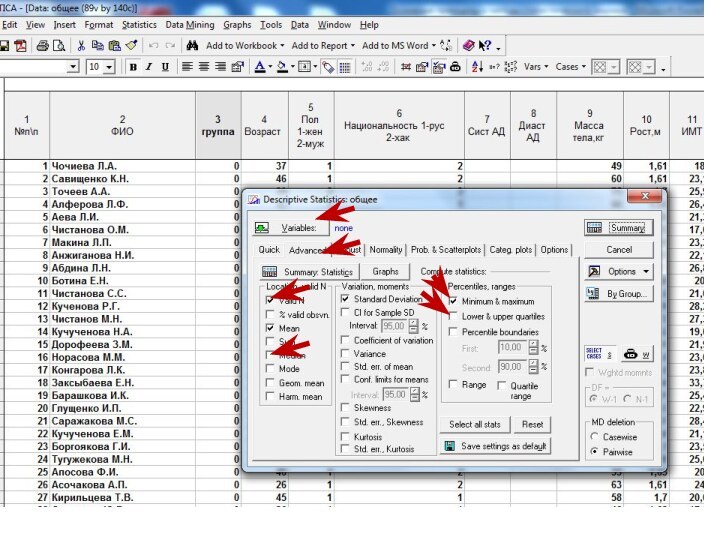
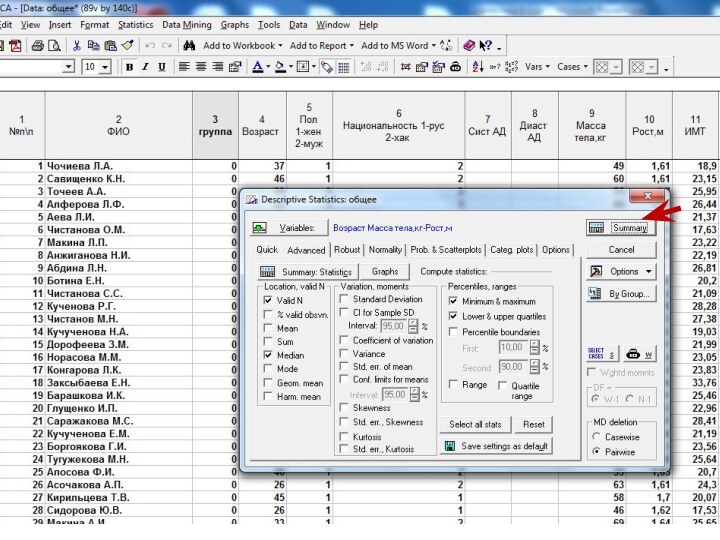
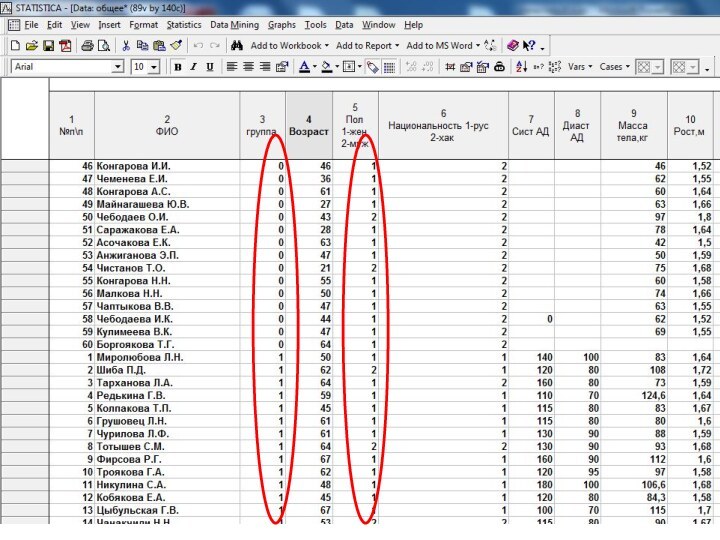

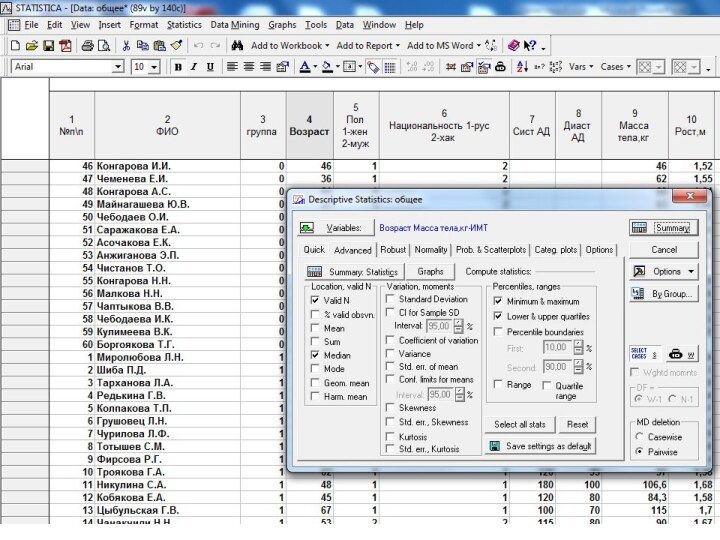















Слайд 7 Выявление закономерностей на выборке производится обычно путем решения
задач, для решения которых существуют соответствующие статистические методы
Слайд 8 Выявление закономерностей на выборке производится обычно путем решения
задач, для решения которых существуют соответствующие статистические методы
Слайд 9
Статистический анализ основан на допущении: то, что
верно для случайной выборки, верно и для генеральной совокупности
(популяции), из которой эта выборка получена
Слайд 10
Распределение признака
Распределением признака в выборке называется совокупность частот
наблюдений для каждого интервала значений признака в конкретной выборке
Распределение
признака в генеральной совокупности (популяции) называется совокупность частот наблюдений для каждого интервала значений признака в популяции
Слайд 13
Теоретическое распределение
Теоретическое распределение можно описать с помощью математической
модели
Распределение частот признака в различных интервалах описывается функцией плотности
распределения.Когда эмпирическое наблюдение аппроксимирует некоторое теоретическое распределение, то можно применить некоторые знания об этом распределении для того чтобы ответить на вопросы относительно полученных в исследовании данных (описание и сравнение данных, моделирование).
Слайд 15
Важно!
Уметь отличать нормально распределенные данные от других видов
распределения, так как от этого зависит выбор методов описания
и сравнения данныхПроверить нормально или нет распределены признаки возможно:
с помощью статистических программ (самый точный подход)
Построив гистограмму распределения эмпирических данных, рассчитав медиану и среднее выборочного распределения (приблизительная оценка)
Слайд 16
Важно!
Если при расчетах среднего и стандартного отклонения
(σ), значения σ превышают половину среднего значения, то распределение
в изучаемой выборке не являются нормально распределенными.Нормальное распределение признаков при биомедицинских исследованиях встречается примерно в 20-25% случаях!!!
Слайд 17
Нормальное (гауссовское) распределение
Функция плотности распределения вероятности:
Определяется двумя параметрами:
среднее (μ) и дисперсия (σ2)
Колоколообразна (унимодальна)
Симметрична относительно среднего
Среднее арифметическое
равно медианеСлайд 18 Представление данных описательной статистики в зависимости от вида
распределения
Мера положения – общее понятие для числового выражения локализации
(на числовой оси), которое описывает типичный результат измеренияМера рассеяния - общее понятие, которое описывает величину, характеризующую разброс (или вариабельность) данных выборочной группы
Слайд 19
Медиана
Медиана:
Не определяется алгебраически
Делит ряд упорядоченных данных пополам. Если
количество наблюдений нечетное, то медиана определяется как наблюдение в
упорядоченном ряду данных, имеющее порядковый номер (n+1)/2. Если четное, то как среднеарифметическое м/у двух соседних средних наблюдений в упорядоченном ряду.
Слайд 20
Процентили
Что такое процентили?
Расположим наши данные упорядочено
Величина Х, до
которой расположен 1% всех наблюдений, находящихся ниже Х, называется
1-ый процентильВеличины Х, которые делят упорядоченный набор значений на 10 равных групп – 10-й, 20-й, …, 90 процентили
Величины Х, которые делят упорядоченный набор на 4 равные группы, 25-й, 50-й, 75-й перцентили, называются квартили. 50-й процентиль – это медиана.
Слайд 21
Общее свойство медианы и перцентилей
Не искажаются ассиметрией распределения
Не
подвержены влиянию выбросов
Не зависят отразмера выборки
Слайд 39
От свойств выборки к свойствам популяции
Преимущество доверительных интервалов
на критериями значимости состоит в том, что доверительные интервалы
поднимают уровень интерпретации с качественных суждений о роли случая как первых (а иногда единственных) объяснительных шагов до количественно оценки выявленных биологических эффектовK.J.Rothman, 1986
Слайд 40
Доверительный интервал
диапазон значений признака, рассчитанный для какого-либо параметра
по выборке с определенной (доверительной) вероятностью
Слайд 41
Предпочтительность обоснования использования доверительного интервала в медицинских данных
Эффект
от приема лекарств был статистически значимым
Эффект от приема лекарств,
снижающих диастолическое давление, был статистически значимым (р<0.05)Среднее диастолическое давление в получавшей лечение группе снизилось со 100 до 92 мм.рт.ст. (р=0,02)
Препарат снизил диастолическое кровянное давление в среднем на 8 мм.рт.ст., со 100 до 92 мм.рт.ст. (95%ДИ 2-14 мм.рт.ст.)
Слайд 42
Представление данных исследования
Приводите числовые данные с разумной степенью
точности
Средний возраст 22,456 лет 22,5
р=0,00002 р
Слайд 43
Представление данных исследования
Указывая число процентов, всегда добавляйте числитель
и знаменатель соответствующей дроби
25% (650/2598)
33% (30 из 90 пациентов)
12
из 16 кроликов (75%) Если объем выборки больше 100, указывайте число процентов с точностью не более десятых
34,5%
Слайд 44
Представление данных исследования
Если объем выборки меньше 100, указывайте
целое число процентов
35%
Если Вы указываете процентное увеличение величины,
используйте формулу((конечное значение – начальное значение)/(начальное значение))*100
Слайд 45
Представление категориальных данных исследования
Уточняйте знаменатели в отношениях, долях
и процентных соотношениях
Приводите сводку категориальных данных в тексте тогда,
когда число категорий не так велико, чтобы оправдать использование рисунка.
Слайд 46
Представление категориальных данных исследования
Иногда категориальные данные усредняют, нужно
быть внимательными при интерпретации.
Это может быть оправданно при использовании
бальных шкалНе всегда приемлемо при описании тяжести болезни (или шкала тяжести болезни)
Слайд 47
Представление непрерывных данных исследования
Образец презентации
Численность титров антител варьировалась
в пределах от 25 до 347 нг/мл и их
среднее значение (стандартное отклонение (СО)) составляло 110нг/мл (43 нг/мл).Если распределение данных близко к нормальному, то они хорошо описываются с помощью среднего и СО
Численность титров антител варьировалась в пределах от 25 до 347 нг/мл с медианой (интерквартильным размахом), равной 110 нг/мл (от 61 до 159 нг/мл)
Если распределение данных отличается от нормального, то они хорошо описываются медианой и интерквартильным размахом.