Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Решение тригонометрических уравнений при помощи формулы понижения степени.

Содержание

2. Гипотеза На уроках математики мы прошли тригонометрические формулы,
3. Цель Исследовать решения тригонометрических уравнений с помощью формул понижения степени.
4. ЗадачиНайти материал по данной теме.Прорешать уравнения данным
5. Этапы работыэтап: Найти материал
6. Откуда появилось такое название? Причина, видимо, в том,
7. Эти формулы называют также формулами половинного аргумента,
8. Формулы
9. этап: Найти уравнения3cos2x−sin2x=02sin2x+3sinx−2=04cos2x + 16sin 2x -
10. 1 + cos x + sin x = 0cos
11. Cos23x + Cos25x + Cos24x = 3
12. Sin4x + cos4x =
13. этап: Поделиться с классом На одном из элективов
14. Изложили теоретический материал и повторили формулы.
15. Показали ряд примеров решения уравнений способом понижения степени.
16. Предложили классу решить самостоятельно несколько уравнений и помогали им справиться с заданиями.
17. Задали несколько уравнений на дом.
18. этап: сравнить другие способы решения Так же на элективах мы рассматривали другие методы решения тригонометрических уравнений.
19. этап: сделать вывод Способ хорош для решения некоторых
20. Скачать презентацию
21. Похожие презентации

Гипотеза На уроках математики мы прошли тригонометрические формулы, а так же рассмотрели методы решения тригонометрических уравнений, среди которых были уравнения содержащие sin и cos в больших степенях. А можно ли использовать формулы понижения степени для приведения таких

Главная
Разное
Решение тригонометрических уравнений при помощи формулы понижения степени.

Решение тригонометрических уравнений при помощи формулы понижения степени.Авторы: учащиеся 10 класса НОЦ

Гипотеза На уроках математики мы прошли тригонометрические формулы, а так же рассмотрели методы

Цель Исследовать решения тригонометрических уравнений с помощью формул понижения степени.

ЗадачиНайти материал по данной теме.Прорешать уравнения данным способом.Показать примеры решения уравнений данным

Откуда появилось такое название? Причина, видимо, в том, что в левой части обоих

Эти формулы называют также формулами половинного аргумента, поскольку они позволяют, зная значение

этап: Найти уравнения3cos2x−sin2x=02sin2x+3sinx−2=04cos2x + 16sin 2x - 11 = 02tg x +

1 + cos x + sin x = 0cos 2х = cos 6x.cos 4x

Cos23x + Cos25x + Cos24x = 3 + cos 6x + cos

этап: Поделиться с классом На одном из элективов мы рассказывали классу про способ

Изложили теоретический материал и повторили формулы.

Показали ряд примеров решения уравнений способом понижения степени.

Предложили классу решить самостоятельно несколько уравнений и помогали им справиться с заданиями.

этап: сравнить другие способы решения Так же на элективах мы рассматривали другие методы решения тригонометрических уравнений.

этап: сделать вывод Способ хорош для решения некоторых тригонометрических уравнений, особенно таких в

Список литературы:А.Г.Мордкович «Алгебра и начала математического анализа» учебник 10 класс профильный уровень;А.Г.Мордкович

Слайды презентации

Слайд 2 Гипотеза
На уроках математики мы прошли тригонометрические формулы, а

Гипотеза На уроках математики мы прошли тригонометрические формулы, а так же рассмотрели

так же рассмотрели методы решения тригонометрических уравнений, среди которых

были уравнения содержащие sin и cos в больших степенях. А можно ли использовать формулы понижения степени для приведения таких уравнений к более простому виду?

Слайд 3 Цель
Исследовать решения тригонометрических уравнений с помощью формул понижения

степени.

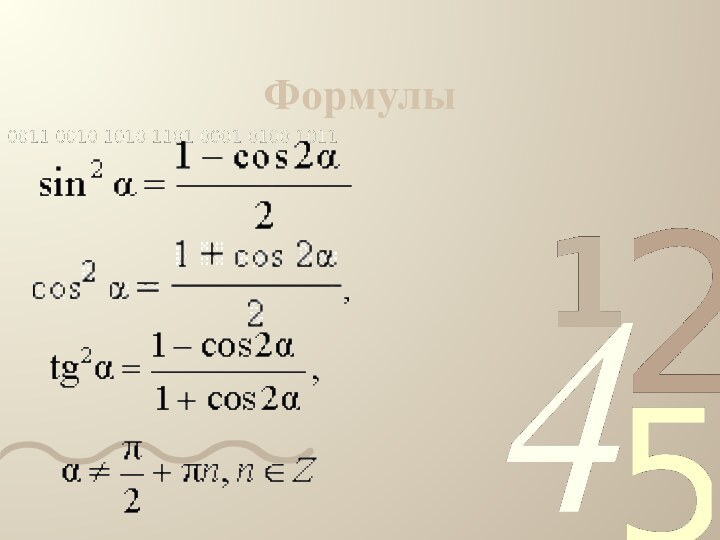
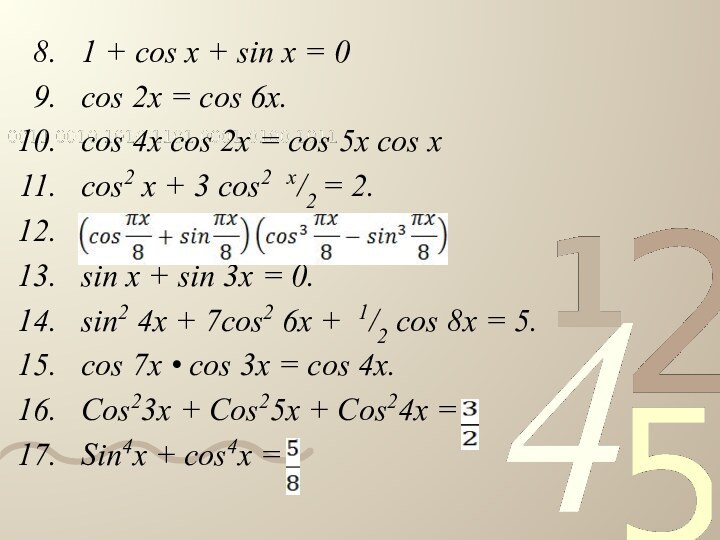
Слайд 4 Задачи
Найти материал по данной теме.
Прорешать уравнения данным способом.
Показать

ЗадачиНайти материал по данной теме.Прорешать уравнения данным способом.Показать примеры решения уравнений

примеры решения уравнений данным способом.
Посмотреть другие способы решения тригонометрических

уравнений.
Поделиться с классом.
Исследовать рациональность решения тригонометрических уравнений с помощью формул понижения степени.

Слайд 5 Этапы работы
этап: Найти материал

Слайд 6 Откуда появилось такое название?
Причина, видимо, в том, что

Откуда появилось такое название? Причина, видимо, в том, что в левой части

в левой части обоих тождеств содержится вторая степень cos

x или sin x, а в правой части – первая степень cos x (степень понизилась). Но при применении этих формул надо быть внимательным: степень понижается, зато аргумент удваивается.

Слайд 7 Эти формулы называют также формулами половинного аргумента, поскольку

Эти формулы называют также формулами половинного аргумента, поскольку они позволяют, зная

они позволяют, зная значение cos x, найти значение синуса

и косинуса половинного аргумента .

Слайд 8 Формулы

Слайд 9 этап: Найти уравнения
3cos2x−sin2x=0
2sin2x+3sinx−2=0
4cos2x + 16sin 2x - 11

= 0
2tg x + 3ctg x = 5
3 cos

2x = 7 sin x.
2sin2 x + cos2 x = 3/2 sin 2x
tg x + tg (π/4 + x ) = -2.

Слайд 10 1 + cos x + sin x = 0
cos 2х

1 + cos x + sin x = 0cos 2х = cos 6x.cos

= cos 6x.
cos 4x cos 2x = cos 5x

cos x
cos2 x + 3 cos2 x/2 = 2.
.
sin x + sin 3x = 0.
sin2 4x + 7cos2 6x + 1/2 cos 8x = 5.
cos 7x • cos 3x = cos 4x.
Cos23x + Cos25x + Cos24x =
Sin4x + cos4x =

Слайд 11 Cos23x + Cos25x + Cos24x =

3 +

cos 6x + cos 10x + cos 8x =

3
cos 6x + cos 10x + cos 8x = 0
cos 6x + cos 10x = 2 cos 8x cos 2x
2 cos 8x cos 2x + cos 8x = 0
cos 8x (2 cos 2x + 1) = 0
2 cos 2x = -1
cos 2x = -
2x = x =