- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Решение возвратных уравнений
Содержание
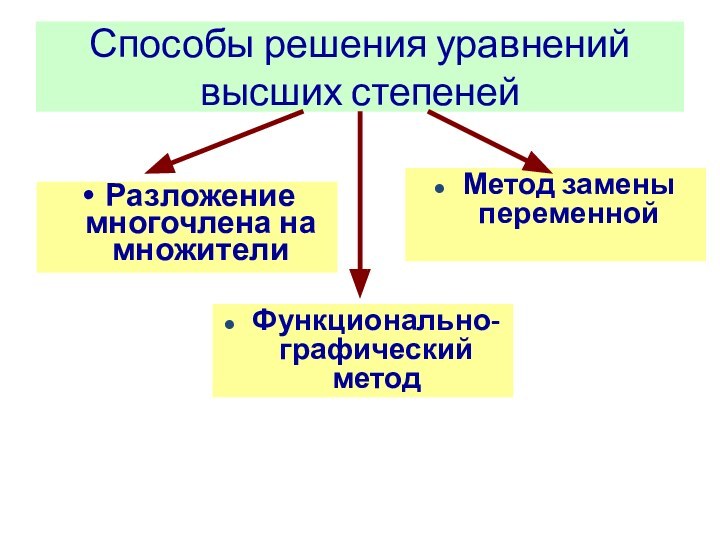
- 2. Способы решения уравнений высших степенейРазложение многочлена на множители Метод замены переменной Функционально-графический метод
- 4. Возвратные уравненияВозвратное уравнение – алгебраическое уравнениеа0хn +
- 5. Уравнения, у которых коэффициенты членов, равноудаленных от
- 6. Алгоритм решения уравнений
- 7. 6х4-35х3+62х2-35х+6=0 Т.к, конечно, х≠0,
- 10. х4 – 5х3 + 8х2 – 5х + 1 = 0
- 11. х4 – 5х3 + 8х2 – 5х + 1 = 0 х4-5х3 +6х2-5х+1=0
- 12. х4-5х3 +6х2-5х+1=0
- 13. х4 – 5х3 + 8х2 – 5х + 1 = 0
- 14. Х4+х3-4х2+х +1=0
- 15. 3х4 + 5х3 – 14х2 -10х + 12=0
- 16. 5х3 + 21х2+21х +5=0 симметрическое уравнение
- 17. Скачать презентацию
- 18. Похожие презентации
Способы решения уравнений высших степенейРазложение многочлена на множители Метод замены переменной Функционально-графический метод






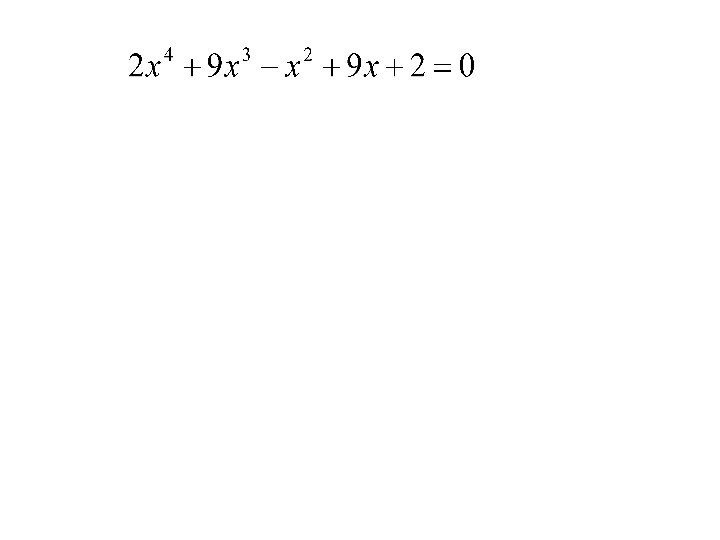

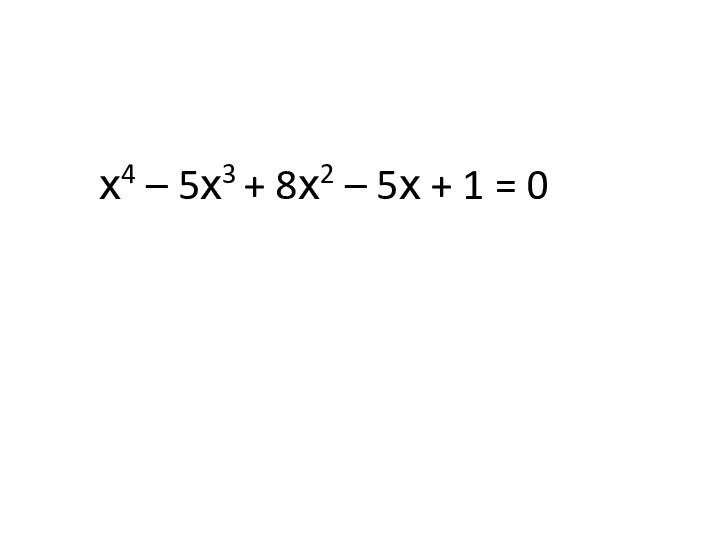
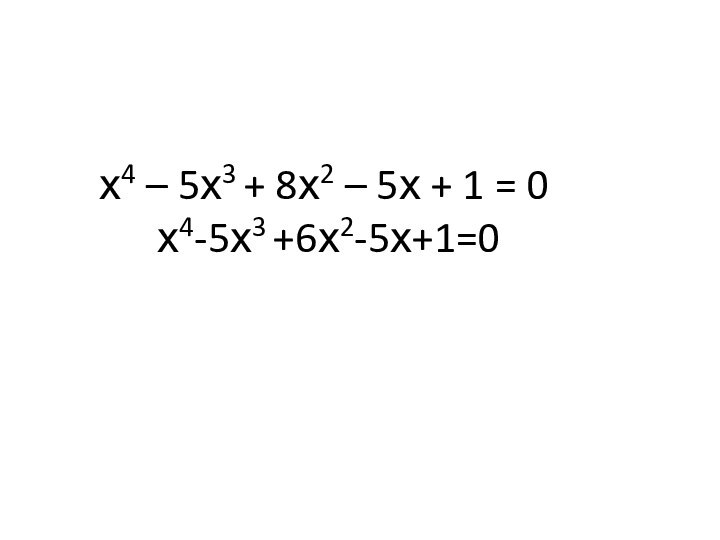






Слайд 4
Возвратные уравнения
Возвратное уравнение – алгебраическое уравнение
а0хn + a1xn
– 1 + … + an – 1x +an=0,
в котором ак = an – k,где k = 0, 1, 2 …n, причем, а ≠ 0.
Задачу нахождения корней возвратного уравнения сводят к задаче нахождения решений алгебраического уравнения меньшей степени. Термин возвратные уравнения был введён Л. Эйлером.
Слайд 5 Уравнения, у которых коэффициенты членов, равноудаленных от «начала»
и «конца» уравнения, равны между собой, называются симметричными.
6х4-35х3+62х2-35х+6=0 Симметричные уравнения четвертой степени.
1)Если m = 1, то это симметричное уравнение первого рода, имеющее вид
ax4 + bx3 + cx2 + bx + a = 0 и решающееся новой подстановкой y =
2) Если m = -1, то это симметричное уравнение второго рода, имеющее вид
ax4 + bx3 + cx2 - bx + a = 0 и решающееся новой подстановкой y =
Слайд 7
6х4-35х3+62х2-35х+6=0
Т.к, конечно, х≠0, то
разделим на х2:
6х2 - 35х + 62 -
35/х + 6/х2 = 0. Сгруппируем члены с одинаковыми коэффициентами:
6(х2 + 1/х2) - 35(х + 1/х) + 62 = 0.
Если х+1/х = у, то (х+1/х)2=у2; х2+1/х2= у2-2;
6(у2 - 2) - 35у + 62 = 0; 6у2 - 35у + 50=0; у1=5/2; у2=10/3;
х + 1/х =5/2 и х + 1/х =10/3
Решая эти уравнения, получим: х1=1/2; х2=2; х3=1/3; х4=3.





























