Презентация на тему Решение заданий №6 (трапеция)по материалам открытого банка задач ЕГЭ по математике 2016 годаhttp://mathege.ru/or/ege/main

стороны равны 20. Найдите синус острого угла трапеции.
Ответ: 0,8.
№

Решение.

острого угла трапеции равен 0,2. Найдите боковую сторону.
Решение.
АН =

Ответ: 10.

№ 45711

Тангенс острого угла равен 7/13. Найдите высоту трапеции.
№ 45839
Решение.

трапеции равна 27. Тангенс острого угла равен 0,9. Найдите

№ 45895

Решение.

Высота трапеции равна 11,4. Найдите тангенс острого угла.
Решение.
№

а ее периметр равен 20. Найдите площадь трапеции.
Решение.
№ 57155

2 и 12, большая боковая сторона составляет с основанием

Решение.

№ 57205

а ее площадь равна 40. Найдите периметр трапеции.
Решение.
№ 61353

Ее площадь равна 44. Найдите острый угол этой трапеции.

Решение.

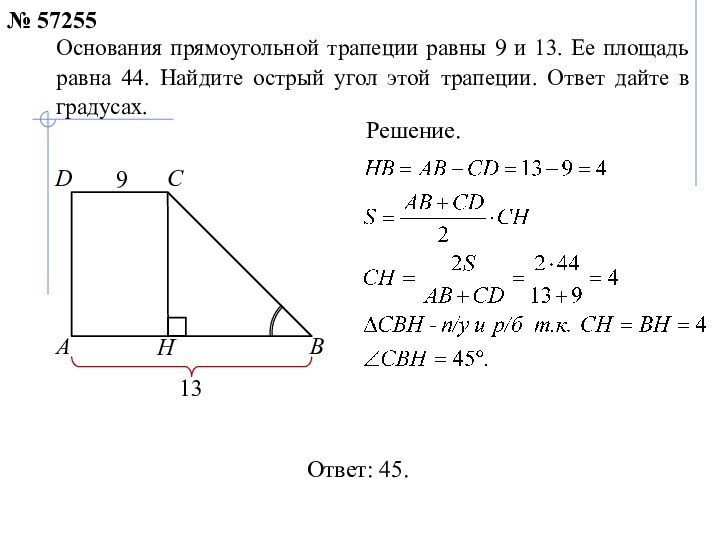
№ 57255

а ее площадь равна 96. Найдите боковую сторону трапеции.
Решение.
№

сторона равна 12. Площадь трапеции равна 114. Найдите острый

Решение.

№ 57355

а ее боковые стороны равны 5. Найдите площадь трапеции.
Решение.
№

сторона, равная 8, образует с одним из оснований трапеции

Решение.

№ 61453

больший из отрезков, на которые делит среднюю линию этой

Решение.

№ 508408

боковая сторона равна 11, угол между ними 60°. Найдите

Решение.

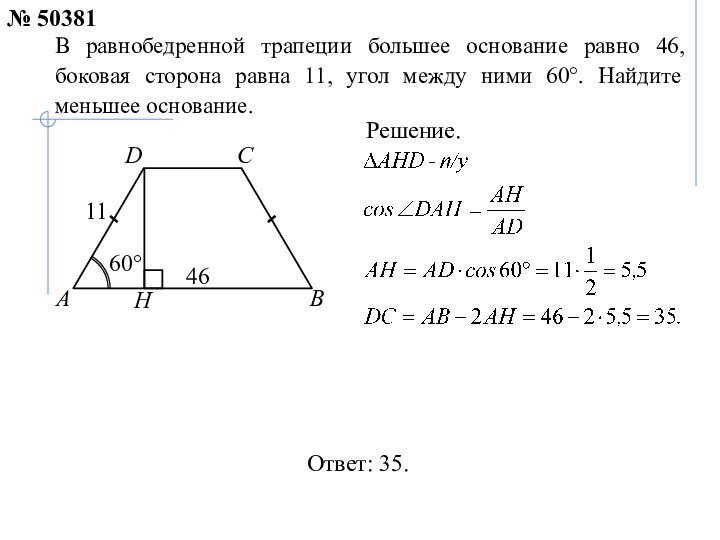
№ 50381

60°

47, острый угол равен 60°. Найдите ее периметр.
Решение.
№ 50431
60°

конец меньшего основания, равного 32, отсекает треугольник, периметр которого

Решение.

№ 50481

A

B

C

D

Е

32

большее основание равнобедренной трапеции, делит его на части, имеющие

Решение.

№ 50531

большее основание равнобедренной трапеции, делит его на части, имеющие

Решение.

№ 50531

один из углов равен 45°. Найдите высоту трапеции.
Решение.
№ 50581

отрезок, соединяющий середины диагоналей трапеции.
Решение.
№ 50879
A
B
C
D
Е
7
18
F
M
N

равна 49. Найдите ее среднюю линию.
Решение.
Если в равнобедренной трапеции

№ 50929

66, средняя линия равна 11. Найдите боковую сторону трапеции.
Решение.
1.

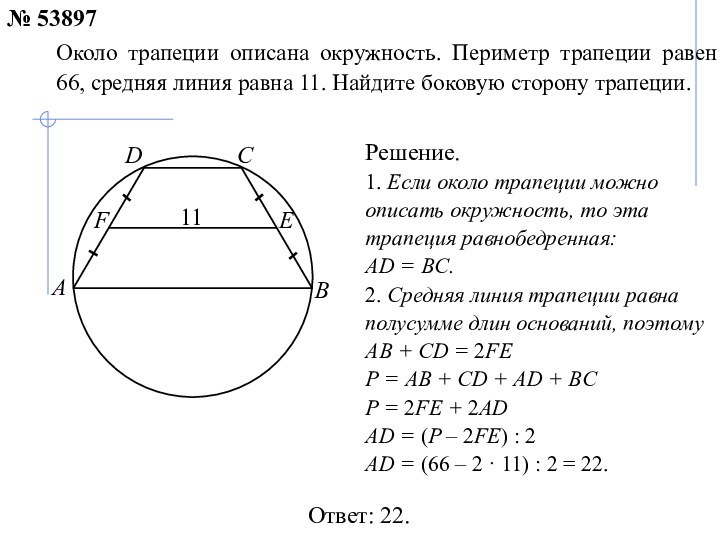
№ 53897

A

B

C

D

11

F

E

основанию, угол при основании равен 60°, большее основание равно

Решение.
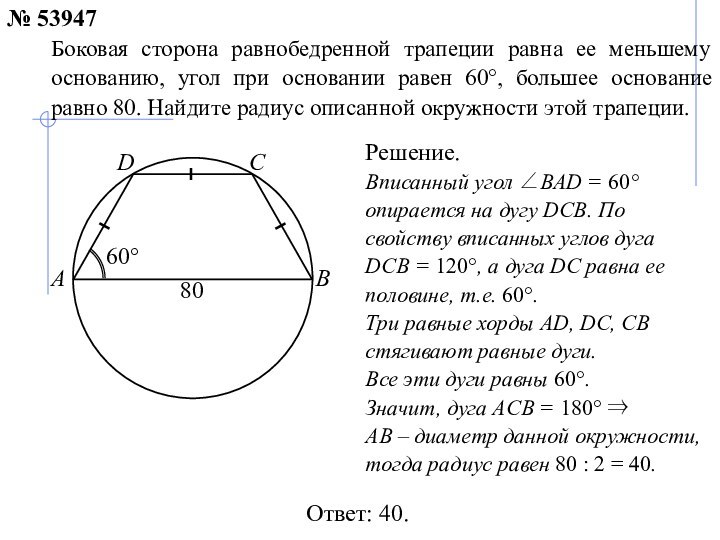
Вписанный угол ВАD = 60° опирается на дугу DCB. По свойству вписанных углов дуга
DCB = 120°, а дуга DC равна ее половине, т.е. 60°.
Три равные хорды AD, DC, CB стягивают равные дуги.
Все эти дуги равны 60°.
Значит, дуга AСB = 180° 
АВ – диаметр данной окружности, тогда радиус равен 80 : 2 = 40.

№ 53947

A

B

C

D

80

60°

Радиус описанной окружности равен 13. Центр окружности лежит внутри

Решение.
ЕН – высота трапеции, проходящая через центр окружности.
Проведем радиусы ОС и ОВ, рассмотрим ∆ЕОС и ∆ОВН – п/у
Тогда по т. Пифагора найдем
ОЕ2 = ОС2 – ЕС2 = 132 – 52 = 122
ОЕ = 12;
ОН2 = ОВ2 – НВ2 = 132 – 122 = 52
ОН = 5;
ЕН = ОЕ + ОН = 12 + 5 = 17.

№ 53963

A

B

C

D

5

12

13

13

Н

Е

О

28 и 4. Найдите среднюю линию трапеции.
Решение.
В четырехугольник можно

№ 54371

88. Найдите длину её средней линии.
Решение.
В четырехугольник можно вписать

№ 54421

100, ее большая боковая сторона равна 37. Найдите радиус

Решение.
В четырехугольник можно вписать окружность тогда и только тогда, если суммы его противоположных сторон равны, т.е.
AB + CD = AD + BC = ½ Р
AD + 37 = ½ · 100 = 50.
AD = 50 – 37 = 13
R = AD : 2 = 6,5.

№ 54449

A

B

C

D

37

12. Синус острого угла трапеции равен 0,8. Найдите боковую

Решение.