Слайд 2
8.1. Типы графов
Ориентированный граф
Неориентированный граф
Слайд 3
8.1. Ориентированный граф
Ориентированный граф G – пара (V,
E), где
V – конечное множество вершин графа G,
V
= {vi}, i = 1, 2, …, n, vi – вершина графа
E – множество ребер графа G; упорядоченные пары вершин из V,
E = {ej}, ei = (u, v), u V, v V,
ei – ребро графа; выходит из вершины u и входит в вершину v
Слайд 4
8.1. Ориентированный граф
Пример: V = {1, 2, 3,
4, 5, 6},
E = {(1,2), (2,2), (2,4), (2,5),
(4,1), (4,5), (5,4), (6,3)}
Слайд 5
8.2. Неориентированный граф
Неориентированный граф G – пара (V,
E), где
V – конечное множество вершин графа G,
V
= {vi}, i = 1, 2, …, n, vi – вершина графа
E – множество ребер графа G; неупорядоченные пары вершин из V,
E = {ej}, ei = (u, v), u V, v V, u v
ei – ребро графа; соединяет вершины u и v
Слайд 6
8.2. Неориентированный граф
Пример: V = {1, 2, 3,
4, 5, 6},
E = {(1,2), (1,5), (2,5), (3,6)}
Слайд 7
8.3. Определения
Если (u, v) – ребро графа G,
тогда вершина u графа – смежная с вершиной v:
u v
Степень вершины в неориентированном графе – число ребер, соединяющих ее с другими вершинами
Вершина со степенью 0 – изолированная
Слайд 8
8.3. Определения
В ориентированном графе: исходящая степень – количество
выходящих из вершины ребер, входящая степень – количество входящих
в вершину ребер
Степень вершины в ориентированном графе = исходящая степень + входящая степень
Слайд 9
8.3. Определения
Путь (маршрут) длины k от вершины u
к вершине v в графе G = (V, E)
– последовательность вершин такая, что u = v0, v = vk и (vi-1, vi) E
для i = 1, 2, …, k
Длина пути – количество составляющих его ребер
Слайд 10
8.3. Определения
Путь содержит вершины v0, v1, …, vk
и ребра (v0, v1), (v1, v2), …, (vk-1, vk)
Если имеется путь p из вершины u в вершину v, говорят, что вершина u достижима из вершины v по пути p
Пусть является простым, если все вершины пути – различны
Слайд 11
8.3. Определения
В ориентированном графе путь
vk> образует цикл, если v0 = vk; цикл простой,
если все вершины v0, v1, …, vk-1 различны
Петля – цикл с длиной 1
В неориентированном графе путь образует (простой) цикл, если k ≥ 3, v0 = vk и все вершины v0, v1, …, vk-1 различны
Граф без циклов – ациклический
Слайд 12
8.3. Определения
Взвешенный граф – граф, с каждым ребром
которого связан определенный вес, обычно определяемый весовой функцией w:
E R
Слайд 13
8.4. Представление графа
1. Набор списков смежных вершин
Для взвешенных
графов вес ребра (u, v) хранится вместе с вершиной
v в списке смежности u
Слайд 14
8.4. Представление графа
Пример – неориентированный граф
Слайд 15
8.4. Представление графа
Пример – ориентированный граф
Слайд 16
8.4. Представление графа
2. Матрица смежности
Слайд 17
8.4. Представление графа
Пример – неориентированный граф
Слайд 18
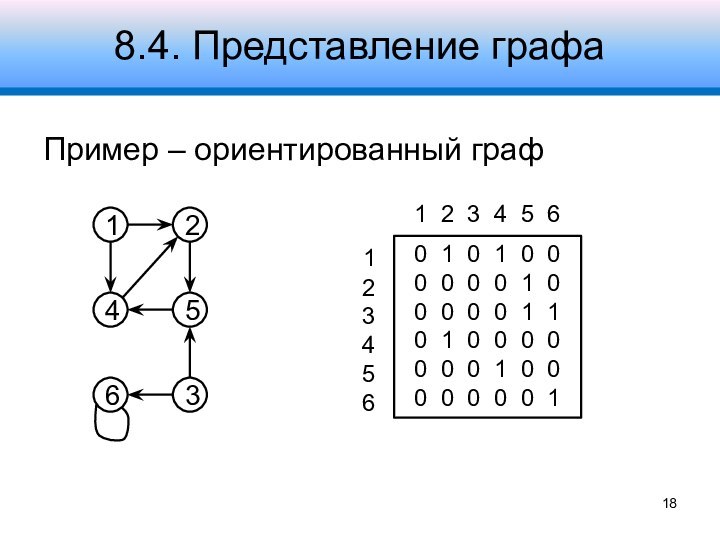
8.4. Представление графа
Пример – ориентированный граф
Слайд 19
8.5. Поиск в ширину
Один из простейших алгоритмов
обхода графа
Задан граф G = (V, E)
Выделена исходная вершина
s
Находятся все вершины, достижимые из s
Строится дерево поиска в ширину с корнем s
Слайд 20
8.5. Поиск в ширину
Окрашивание вершин графа:
белые –
еще не открытые вершины,
серые и черные – открытые вершины,
которые обрабатываются по-разному:
вершины, смежные с черной, серые или черные;
вершины, смежные с серой, могут быть белыми
Слайд 21
8.5. Поиск в ширину
Корень дерева – s
Сканируется
список смежности открытой вершины u : если открывается белая
вершина v, то вершина v и ребро (u, v) добавляются в дерево
u – предшественник (или родитель) v в дереве поиска вширь, v – потомок u
Слайд 22
8.5. Алгоритм поиска BFS(G, s)
Обозначения:
Adj[u] – список смежности
для вершины u
color[u] – цвет вершины u
pred[u] – предшественник
вершины u; если предшественника нет, pred[u] = NULL
d[u] – расстояние от s до вершины u
Q – очередь для работы с множеством серых вершин
Слайд 23
8.5. Алгоритм поиска BFS(G, s)
Инициализация:
Для каждой вершины u
V[G], кроме s {
color[u] = белый
d[u] =
pred[u]
= NULL
}
color[s] = серый
d[s] = 0
pred[s] = NULL
Записать s в очередь Q
Слайд 24
8.5. Алгоритм поиска BFS(G, s)
while Q не пуста
{
u = очередная вершина из Q
для каждой v
Adj[u]
if color[v] = белый {
color[v] = серый
d[v] = d[u] + 1
pred[v] = u
Записать v в Q
}
color[u] = черный
}
Слайд 27
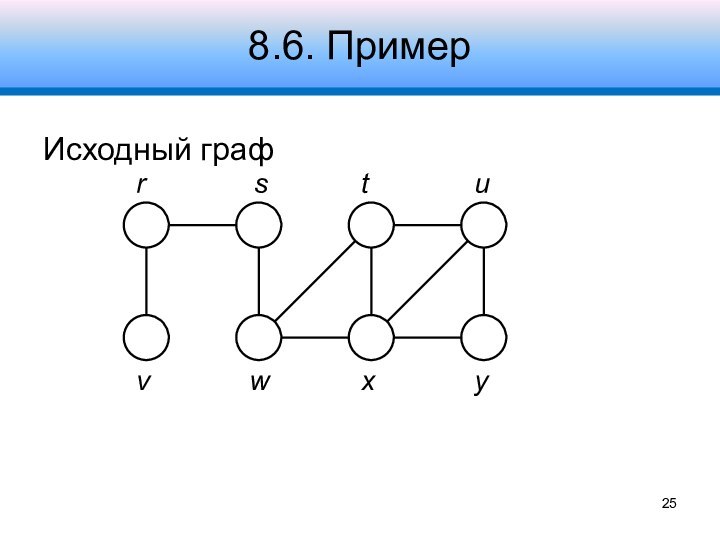
8.6. Пример
1-я итерация цикла while
Слайд 28
8.6. Пример
2-я итерация цикла while
1
2
2
Слайд 29
8.6. Пример
3-я итерация цикла while
2
2
2
Слайд 30
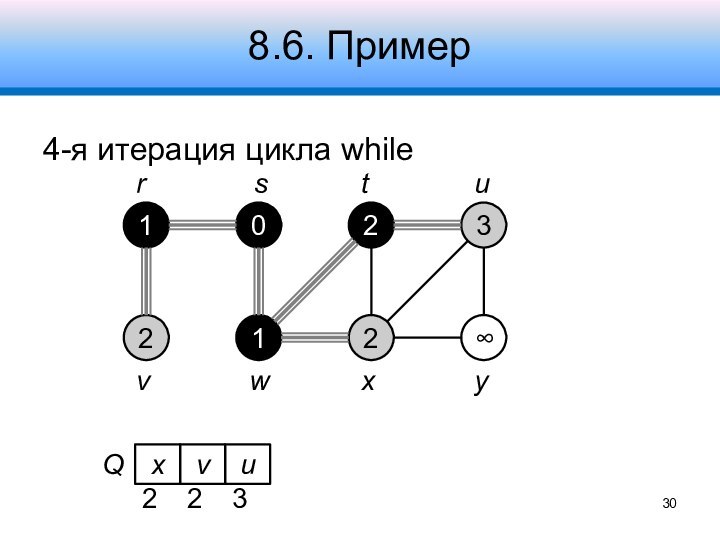
8.6. Пример
4-я итерация цикла while
2
2
3
Слайд 31
8.6. Пример
5-я итерация цикла while
2
3
3
Слайд 32
8.6. Пример
6-я итерация цикла while
3
3
Слайд 33
8.6. Пример
7-я итерация цикла while
3
Слайд 34
8.6. Пример
8-я итерация цикла while
Слайд 36
8.7. Анализ алгоритма
Общее время операций с очередью –
Ο(V)
Сумма длин всех списков смежности – (E)
Общее время сканирования списков –
Ο(E)
Накладные расходы на инициализацию – Ο(V)
Общее время работы алгоритма BFS –
Ο(V + E)




















![Сеть 8.5. Алгоритм поиска BFS(G, s)Обозначения:Adj[u] – список смежности для вершины ucolor[u] –](/img/tmb/14/1365760/57793edb76cbbcf96fe27e297286cff3-720x.jpg)
![Сеть 8.5. Алгоритм поиска BFS(G, s)Инициализация:Для каждой вершины u V[G], кроме s](/img/tmb/14/1365760/3bc2f27b734bf45950b15bc037d05c27-720x.jpg)