Слайд 2
Понятие множества
Под множеством понимается совокупность некоторых объектов. Объекты,
которые образуют множество, называются элементами или точками, этого множества.
Множества обозначаются прописными буквами, а их элементы – строчными.
- принадлежит
- не принадлежит
- подмножество
Ø - пустое множество
Слайд 3
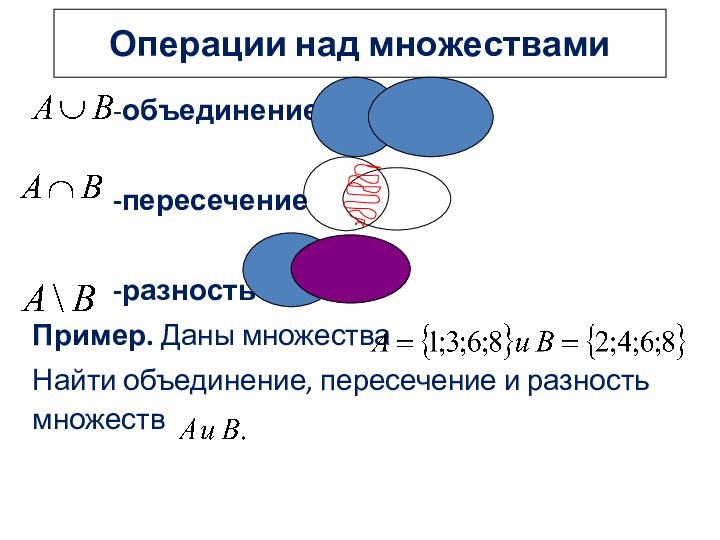
Операции над множествами
-объединение
-пересечение
-разность
Пример. Даны множества
Найти объединение, пересечение и разность множеств
Слайд 4
Последовательность. Предел последовательности.
Определение 1. Если по некоторому закону
каждому натуральному числу
поставлено в соответствие вполне определенное число , то говорят, что дана числовая последовательность :
словами, числовая последовательность эта функция натурального аргумента
называются членами последовательности, а число общим членом.
Пример.
Слайд 5
Определение 2. Число A называется пределом числовой последовательности
, если для любого сколь
угодно малого положительного числа , найдется такой номер N , зависящий от , что для всех членов последовательности с номерами справедливо
Предел числовой последовательности обозначается
или
Последовательность, имеющая предел, называется
сходящейся, а в противном случае - расходящейся.
Слайд 6
Функция. Способы задания функции.
Определение 3. Если каждому элементу
х из множества X по некоторому правилу
соответствует единственный элемент у из множества Y , то говорят, что на множестве X задана функция переменной х . При этом множество X называется областью
определения функции, а множество Y –
областью значений функции.
x- называется независимой переменной или
аргументом, у - зависимой переменно, буква f – обозначает закон соответствия.
Слайд 7
Существует несколько способов задания функции.
Аналитический способ, если
функция задана формулой вида
.
Табличный способ, если функция задана в виде таблицы.
Графический способ, если функция изображена в виде в виде графика-множества точек плоскости, абсциссой которых есть значения аргумента , о ординаты - соответствующие им значения функции .
Словесный способ, если функция описана правилом ее составления, например функция Дирихле: если рационально; и
если нерационально.
Слайд 8
Функция может быть задана программой, вычисляющей ее значения
с помощью компьютера.
Основные свойства функций.
1. Четность и нечетность.
Функция
называется четной, если для любых значений
из любой области определения и нечетной, если
Функция, не являющаяся ни четной, ни нечетной, называется функцией общего вида.
График четной функции симметричен относительно оси ординат.
График нечетной функции симметричен относительно начала координат.
Слайд 9
2. Монотонность. Функция
называется возрастающей (убывающей) на
промежутке X, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.
Функции возрастающие или убывающие
называются монотонными.
3. Ограниченность. Функция называется ограниченной на промежутке X, если существует такое положительное число
что для любого
В противном случае функция называется
неограниченной.
Слайд 10
4. Периодичность. Функция
называется периодической с периодом
если для любых из области определения
функции
Слайд 11
Основные элементарные функции
1) Степенная функция:
,
где
Ее область определения и множество значений зависят от α .
Например:
а)
б)
в)
Слайд 12
2. Показательная функция:
где
3) Логарифмическая функция:
где
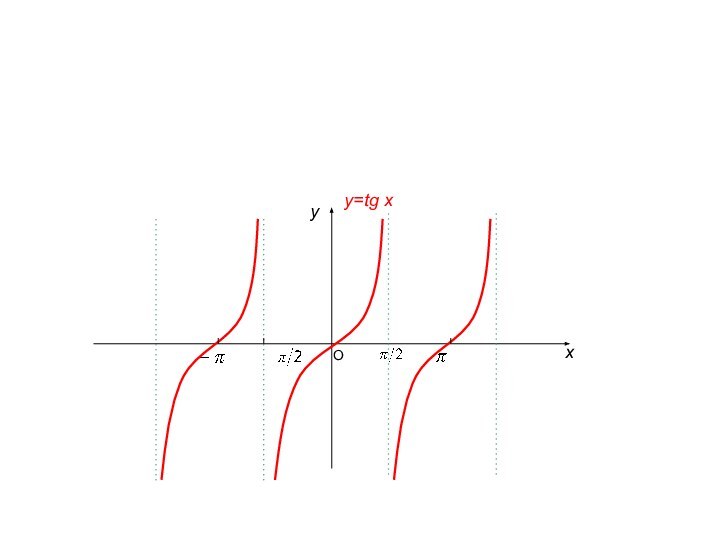
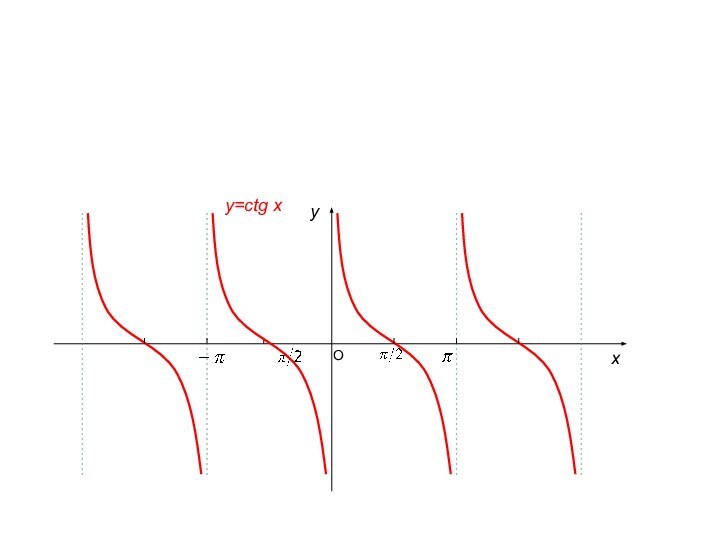
4) Тригонометрические функции:
а)
б)
в)
г)
Слайд 13
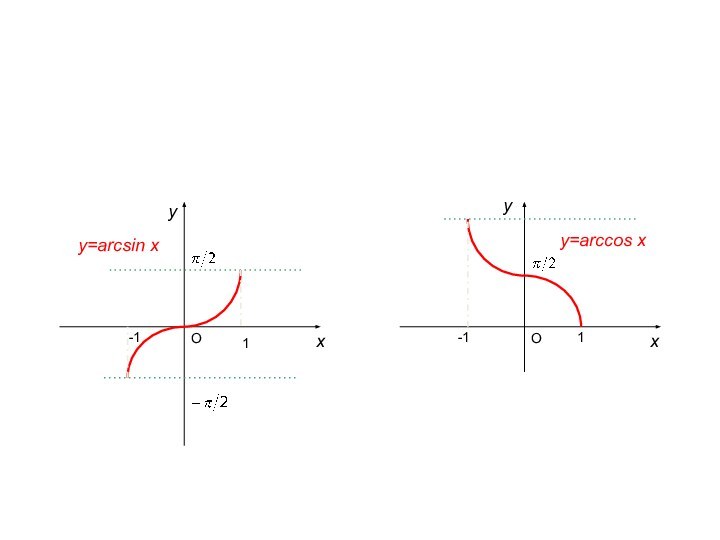
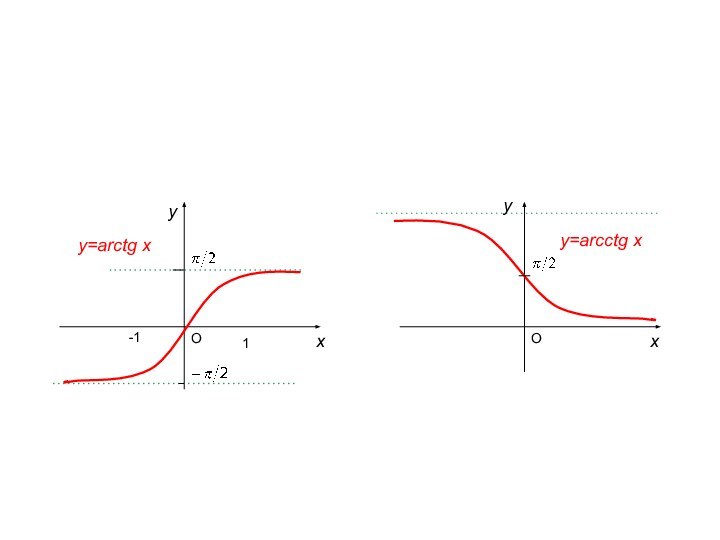
5) Обратные тригонометрические функции:
а)
,
Слайд 14
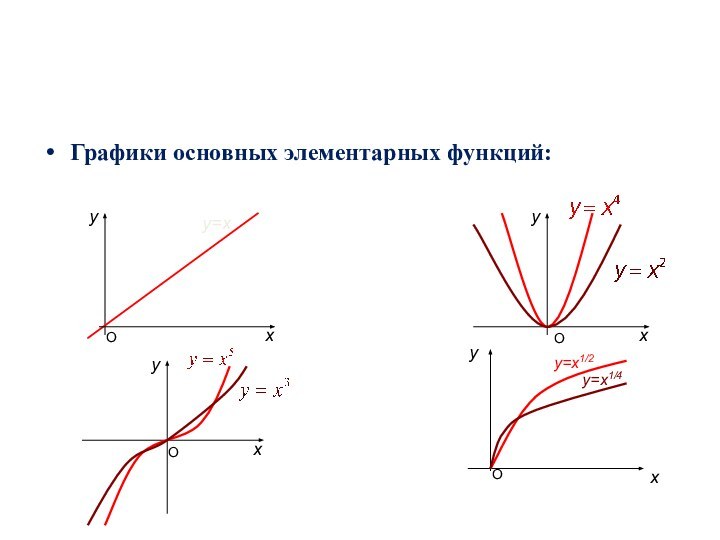
Графики основных элементарных функций:
у=х
у
х
О
у
х
О
у
у
х
х
О
О
у=х1/2
у=х1/4
Слайд 15
Графики основных элементарных функций:
у=х1/3
у=х1/5
у
у
у
у
х
х
х
х
у=
О
О
О
О
у=
1
у=ax (0а1)
у=ax
(а>1)
Слайд 16
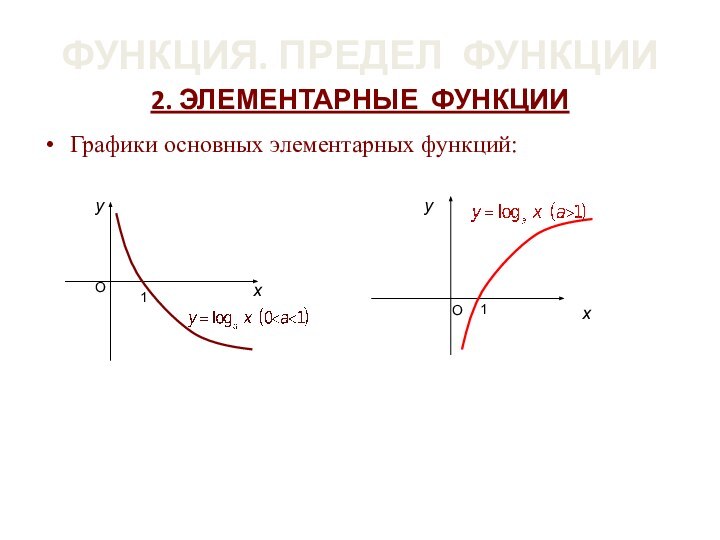
ФУНКЦИЯ. ПРЕДЕЛ ФУНКЦИИ
2. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
Графики основных элементарных
функций:
х
х
у
у
О
О
1
1
Слайд 17
1
-1
у
х
О
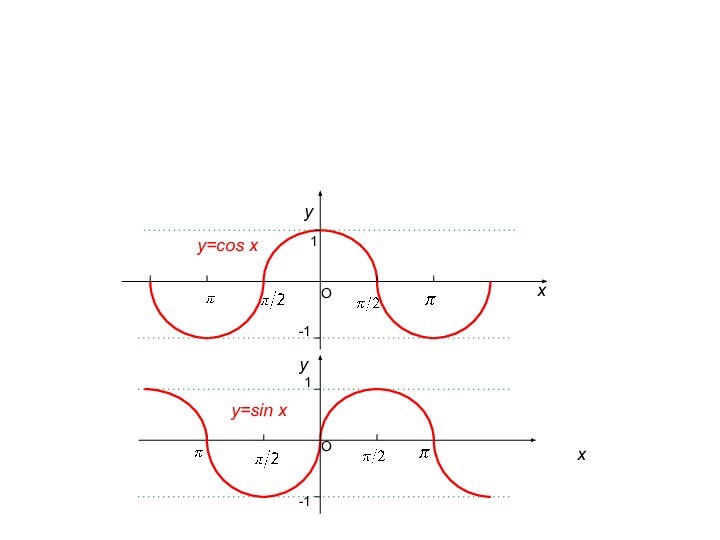
y=соs x
х
О
1
-1
y=sin x
у
Слайд 20
1
-1
у
х
х
у
О
О
-1
1
у=arcsin x
у=arccos x