Презентация на тему Случайные величины и их характеристики

оперировать не понятием случайного события, для которого существуют только

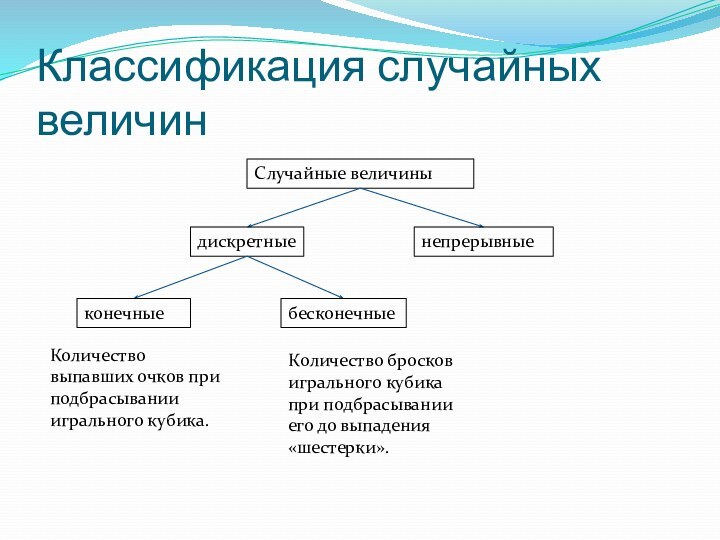
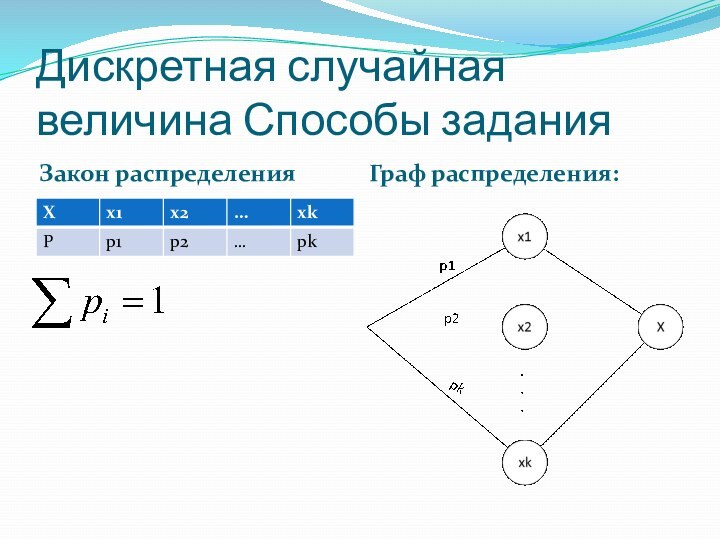
две возможности: оно может произойти или не произойти в результате опыта, а понятием так называемой случайной величины.
Величина называется случайной, если при проведенном испытании может принимать различные значения, причем заранее не известно, какие именно.
Например, при подбрасывании игрального кубика может выпасть любая грань с числом точек от 1 до 6.

представляет собой конечное или счетное множество, она называется дискретной

случайной величиной.
Например, количество выпавших очков при подбрасывании игральной кости.
Если эти значения заполняют целиком некоторый интервал — непрерывной случайной величиной.
Например, время прихода студента на лекцию.

игрального кубика.
Количество бросков
игрального кубика при подбрасывании его до

выпадения «шестерки».

определяется своими значениями х1, х2... и их вероятностями p1,

p2….
Если случайная величина непрерывна, то эта величина X определяется областью своих значений и функцией распределения F(x), выражающей вероятность того, что X принимает какое-либо значение (безразлично какое именно), меньшее, чем х, т. е. F(х)=Р(Х<х). Производная этой функции F'(x) называется функцией плотности вероятности или дифференциальной функцией распределения и обозначается f(х).

отклонение

(историческое).
Математическое ожидание – это среднее значение случайной величины с

учетом вероятностей.

для которого вероятность максимальна

Медиана – это такое значение случайной

величины, для которого процесс почти равновозможно закончится до него и после него, т.е.

ожидания, является дисперсия — математическое ожидание квадрата отклонения от

среднего:

отклонения случайной величины от математического ожидания и вычисляется как

выпавших шестерок}. Построить закон распределения этой случайной величины и

найти все характеристики.