Презентация на тему Спектры сигналов. Преобразование Фурье

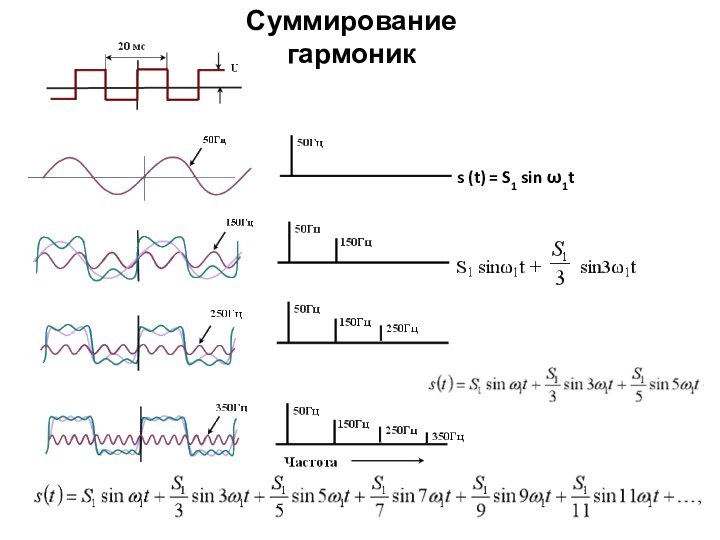
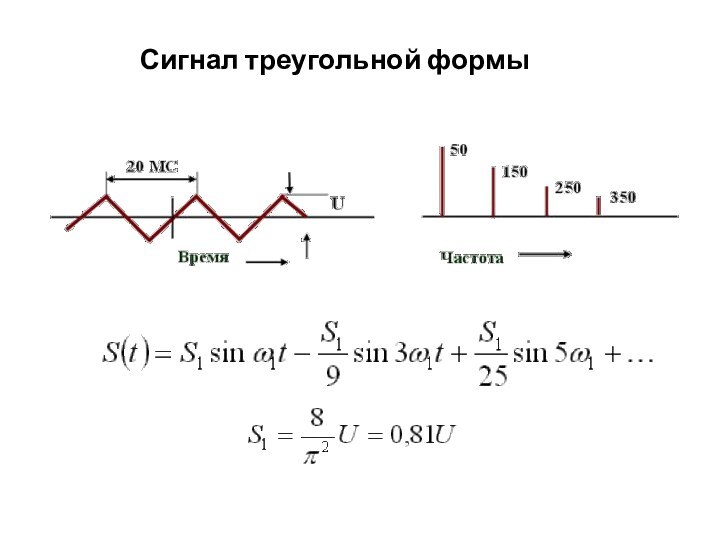
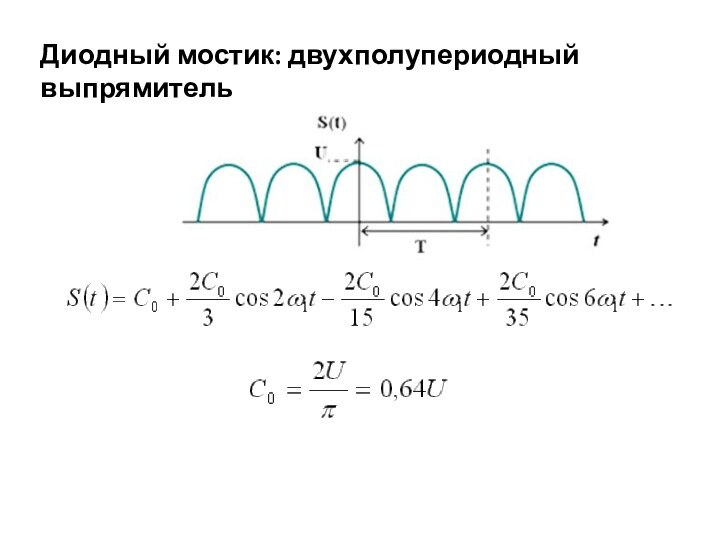
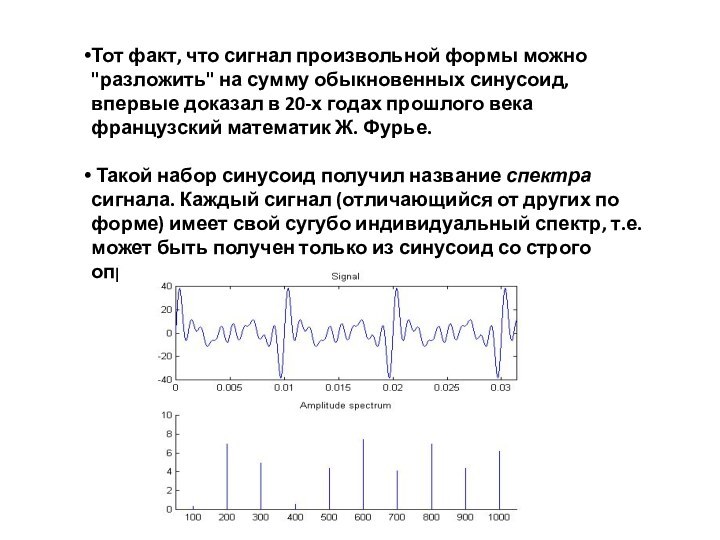
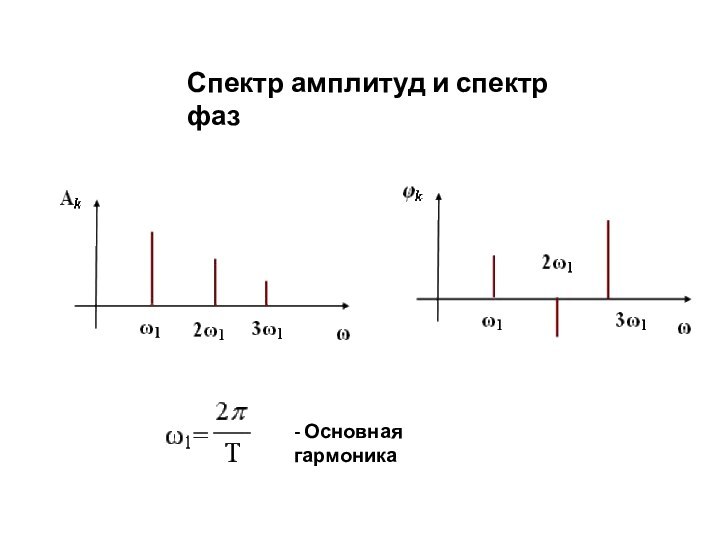
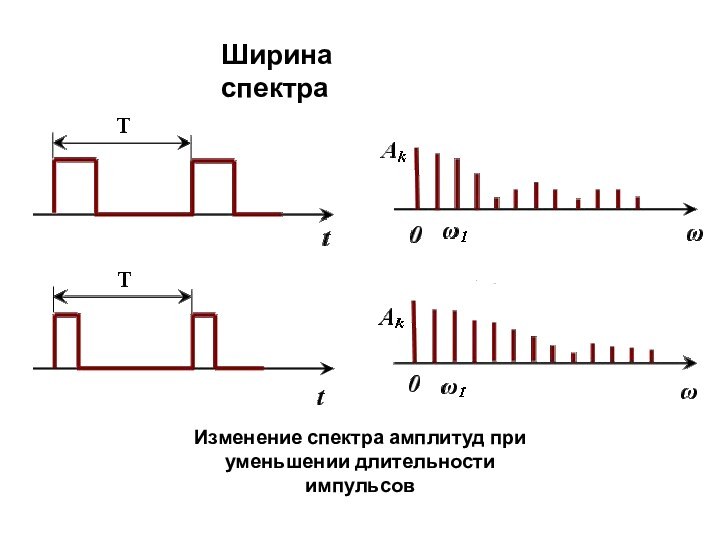
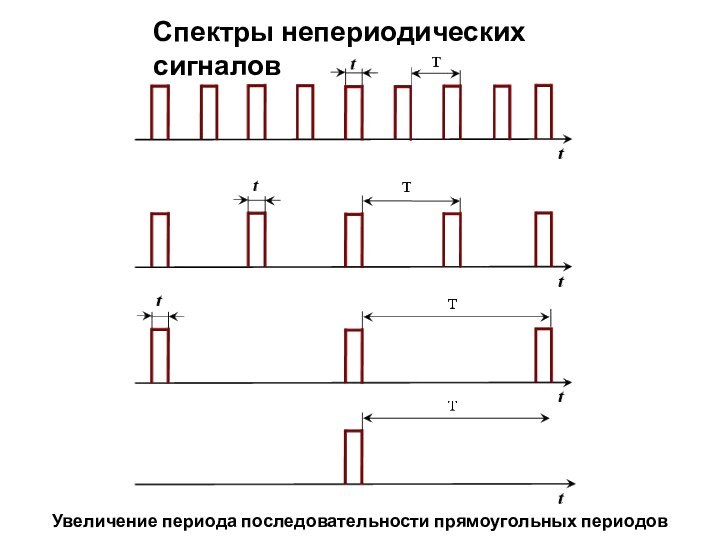
периодический сигнал
Другой пример периодического сигнала – последовательность прямоугольных импульсов

Каким образом последовательность
прямоугольных импульсов
можно представить через гармонические сигналы?

синусоид, так и из косинусоид

Используем известное тригонометрическое соотношение

Выражение показывает, что любой периодический сигнал состоит из гармоник.

в результате суммирования бесконечного числа гармоник с частотами F,

2F, 3F, 4F, …, и специально подобранными амплитудами и фазами

x(t) = A0 + A1sin(2Ft + 1) + A2sin(22Ft + 2) + A3sin(23Ft + 3) + … (и т.д.) ИЛИ

на сумму обыкновенных синусоид, впервые доказал в 20-х годах

прошлого века французский математик Ж. Фурье.

Такой набор синусоид получил название спектра сигнала. Каждый сигнал (отличающийся от других по форме) имеет свой сугубо индивидуальный спектр, т.е. может быть получен только из синусоид со строго определенными частотами и амплитудами.

чем больше пауза между импульсами, тем шире во всех

этих случаях спектр сигнала, т.е. тем медленнее убывают амплитуды гармоник с ростом их номера.

ширина полосы пропускания устройства не должна быть уже ширины спектра сигнала

образом, спектр непериодического сигнала является в общем случае не

дискретным

мощность сигнала равна сумме квадратов коэффициентов Фурье (гармоник сигнала)

в виде



то сама функция может быть представлена с

помощью интеграла Фурье

- это собственная функция устойчивой системы
Если

на входе


То на выходе:

с преобразованием Фурье входа
следующим соотношением:


Поскольку вход и выход можно

описать соотношением

то можно сформулировать свойство свертки: преобразование Фурье свертки двух функций является произведением их преобразований Фурье, т.е.