- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Средние величины
Содержание
- 2. Средние величиныкаждая средняя величина характеризует совокупность по
- 3. Средние величины связаны с законом больших чиселПри
- 4. Важнейшим условием научного использования средних величин в
- 5. Средние величиныВ совокупности с качественно однородными признаками,
- 6. Системные средниесовокупность с качественно разнородными признаками разбивается
- 7. Системные средние (примеры):характеристики государства, единой народнохозяйственной системы:
- 8. Исходное соотношение средней
- 9. Общие принципы применения средних величин:Средняя должна определяться
- 10. Свойство средних величин: сумма индивидуальных значений признака
- 11. Основные понятия:Признак, по которому находится средняя называется
- 12. Виды среднихСтепенныеСтруктурныеАрифметическаяГармоническаяГеометрическаяМодаКвадратическаяМедиана
- 13. Степенные средниев зависимости от представления исходных данных,
- 14. Степенные средние Простая (невзвешенная) средняя считается по
- 15. Виды степенных среднихЕсли рассчитать все виды средних
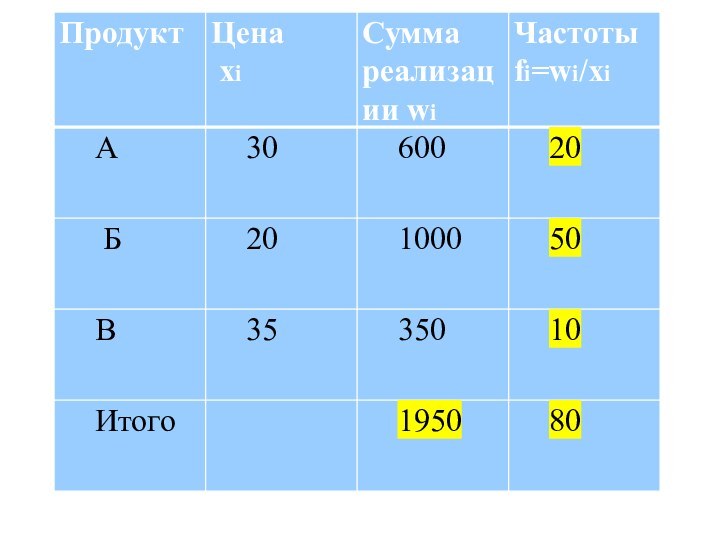
- 17. Для определения ср.цены :х---=∑wi/Σfi=1950 /80=24,3 руб.Если использовать
- 18. ЗАДАНИЕ 1.ИЗУЧИТЬ СВОЙСТВА СРЕДНЕЙ АРИФМЕТИЧЕСКОЙ, ПОЯСНИТЬ НА ПРИМЕРАХ.
- 19. Средняя арифметическая обладает рядом свойств:От уменьшения или
- 20. Пример
- 21. Средний возраст Простая средняяВзвешеннаясредняя
- 22. При расчете средней по интервальному вариационному ряду
- 23. Гармоническая простая2 машины прошли один и тот
- 24. Гармоническая взвешеннаяАвтомобиль прошел первые 210 км со скоростью
- 25. РЕШЕНИЕ: xi – скорость на отрезках пути,fi
- 26. При расчете средней по интервальному вариационному ряду
- 28. Средний возраст рабочих фирмы будет равен:Хср = (25*7+35*13+45*48+55*32+65*6)/106 = 47 лет
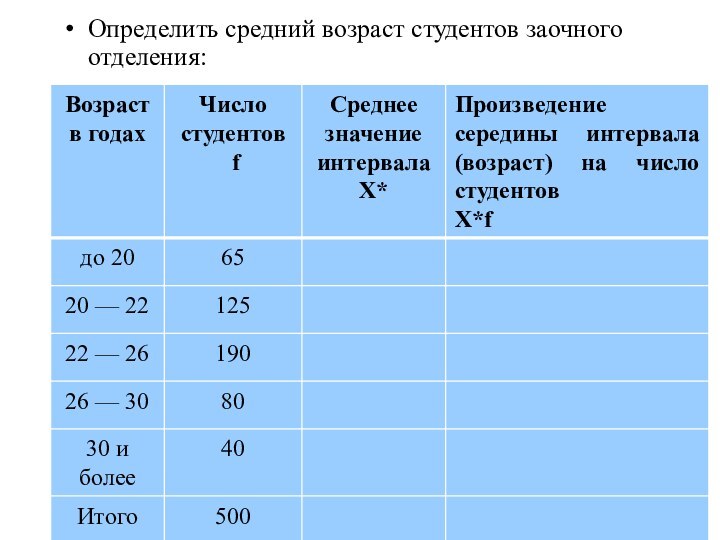
- 29. Определить средний возраст студентов заочного отделения:
- 31. средний возраст студентов заочного отделения:
- 32. Структурные средние применяются для изучения внутреннего строения
- 33. Структурные средние Мода наиболее часто повторяющееся значения
- 34. МОДАРаспределение проданной женской обуви по размерам характеризуется следующим образом:
- 35. Модальный интервал величины стажа 6-8 лет, а мода продолжительности стажа: Мо=6+2(35-20) / (35-20)+(35-11) = 6.77 года
- 36. Структурные средние Медиана величина признака, которая делит
- 37. медианаВ дискретном ряду распределения медиана находится непосредственно по накопленной частоте, соответствующей номеру медианы .
- 38. Дискретный ряд - это такой вариационный ряд, в
- 39. Для варьирующего ряда ( т.е. построенного в
- 40. В таблице показан расход электроэнергии в январе жильцами девяти квартир:
- 42. Скачать презентацию
- 43. Похожие презентации
Средние величиныкаждая средняя величина характеризует совокупность по одному изучаемому признаку. если совокупность характеризуется несколькими признаками, то необходима система средних величин, которая может описать изучаемое явление в целом.
Слайд 2
Средние величины
каждая средняя величина характеризует совокупность по одному
изучаемому признаку.
система средних величин, которая может описать изучаемое явление в целом.
Слайд 3
Средние величины связаны с законом больших чисел
При осреднении
случайные отклонения индивидуальных величин в силу действия закона больших
чисел взаимопогашаются и в средней выявляется основная тенденция развития, необходимость, закономерностьСредняя величина является равнодействующей всех факторов, оказывающих влияние на изучаемое явление, т.е, при расчете средних величин взаимопогашаются влияние случайных (индивидуальных) факторов и, таким образом, возможно определение закономерности, присущей исследуемому явлению.
Слайд 4 Важнейшим условием научного использования средних величин в статистическом
анализе общественных явлений является однородность совокупности, для которой исчисляется
средняя
Слайд 5
Средние величины
В совокупности с качественно однородными признаками, средняя
величина выступает как типическая средняя (обобщает качественно однородные значения признака
в данной совокупности)В совокупности с качественно разнородными признаками средние величины обобщают качественно разнородные значения признаков или системных пространственных совокупностей (международное сообщество, континент, государство, регион, район и т.д.) или динамических совокупностей, протяженных во времени (век, десятилетие, год, сезон и т.д.). Такие средние величины называют системными средними.
Слайд 6
Системные средние
совокупность с качественно разнородными признаками разбивается на
группы, содержащие только однородные элементы;
рассчитываются сначала средние по группам
(групповые средние) – выражают наиболее типичную величину явления в каждой группе;рассчитывается для всех элементов общая средняя величина, характеризующая явление в целом: как средняя из групповых средних, взвешенных по числу элементов совокупности, включенных в каждую группу.
Слайд 7
Системные средние (примеры):
характеристики государства, единой народнохозяйственной системы: средний
национальный (или реальный) доход на душу населения, средняя урожайность
зерновых по стране, среднее потребление продуктов питания на душу населения, средние показатели рождаемости населения по всем регионам страны, средние температуры за определенный период и т.д
Слайд 9
Общие принципы применения средних величин:
Средняя должна определяться для
совокупностей, состоящих из качественно однородных единиц.
Средняя должна исчисляться для
совокупности, состоящей из достаточно большого числа единиц.Средняя должна рассчитываться для совокупности, единицы которой находятся в нормальном, естественном состоянии.
Средняя должна вычисляться с учетом экономического содержания исследуемого показателя.
Слайд 10 Свойство средних величин: сумма индивидуальных значений признака равна
сумме средних величин
Индивидуальная выработка у 5 операционистов коммерческого банка
за день составила 136, 140, 154, 158 и 162 операции (Σ=750). Определить среднее число операций за день, выполненных одним операционистом.Хср.=(136+140+154+158 +162)/5=150
Σ Х ср=150+150+150+150+150 = 750
Слайд 11
Основные понятия:
Признак, по которому находится средняя называется осредняемым
признаком (х---).
Величина осредняемого признака у каждой единице совокупности наз.
индивидуальным его значением (вариантами) – х1,х2…Частоты – абсолютные числа, показывающие столько раз в совокупности встречается данное значение признака (f). Сумма всех частот должна быть равна численности единиц всей совокупности
Слайд 12
Виды средних
Степенные
Структурные
Арифметическая
Гармоническая
Геометрическая
Мода
Квадратическая
Медиана
Слайд 13
Степенные средние
в зависимости от представления исходных данных, могут
быть простыми и взвешенными:
если вариант Х встречается один раз, расчеты проводят по
средней простой, а если вариант повторяется некоторое число раз, то есть имеет разные частоты , то расчет проводят по средней взвешеннойПри расчете средних в качестве весов могут использоваться не только абсолютные, но и относительные величины (частость- отношение частоты к общему количеству исследуемых элементов, т.е. объему совокупности):
di = fi / Σ fi
Слайд 14
Степенные средние
Простая
(невзвешенная)
средняя
считается
по несгруппированным
данным
где Xi - варианта (значение) осредняемого признака;
m - показатель степени средней;n - число вариант (число единиц совокупности).
Взвешенная средняя считается по сгруппированным данным
где Xi - варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта;
m - показатель степени средней;
fi - частота, показывающая, сколько раз встречается i-e значение осредняемого признака (вес)
Слайд 15
Виды степенных средних
Если рассчитать все виды средних для
одних и тех же исходных данных, то значения их
окажутся неодинаковыми. Здесь действует правило мажорантности средних: с увеличением показателя степени m увеличивается и соответствующая средняя величина:
Слайд 17
Для определения ср.цены :
х---=∑wi/Σfi=1950 /80=24,3 руб.
Если использовать не
взвешенное ср.арифметич., то получим средний, который не отражает объема
реализации, т.е.нереальная:х---=30+20+35\3=28,3 руб.
Слайд 19
Средняя арифметическая обладает рядом свойств:
От уменьшения или увеличения
частот каждого значения признака х в n раз величина средней арифметической не
изменится.Если все частоты разделить или умножить на какое-либо число, то величина средней не изменится.
2. Общий множитель индивидуальных значений признака может быть вынесен за знак средней:
3. Средняя суммы (разности) двух или нескольких величин равна сумме (разности) их средних:
4. Если х = с, где с - постоянная величина, то
5. Сумма отклонений значений признака Х от средней арифметической х равна нулю:
Слайд 22 При расчете средней по интервальному вариационному ряду необходимо
найти середину интервалов как полусумму верхней и нижней границ
(значения xi) и количество единиц совокупности в каждой группе fiВ случае открытых интервалов значение нижнего или верхнего интервала определяется по величине интервалов, примыкающих к ним.
Средние, вычисляемые из интервальных рядов являются приближенными.
Слайд 23
Гармоническая простая
2 машины прошли один и тот же
путь.
1-я со скор. 60км\ч, 2-я со скор.80км.\ч.
Средняя скорость
их составит:х---= 2 / (1/60+1/80) =
2 / (60+80)/4800=68.6 км.ч.
Слайд 24
Гармоническая взвешенная
Автомобиль прошел первые 210 км со скоростью 70 км/ч,
а оставшиеся 150 км со скоростью 75 км/ч. Определить среднюю скорость
автомобиля на протяжении всего пути в 360 км.
Слайд 25
РЕШЕНИЕ:
xi – скорость на отрезках пути,
fi –
отрезки пути ,
Σ fi - весь путь,
Σfi/xi
- время затраченное на весь путь Тогда средняя скорость может быть найдена как частное от деления всего пути на общие затраты времени:
Слайд 26 При расчете средней по интервальному вариационному ряду необходимо
сначала найти середину интервалов. Это и будут значения xi, а
количество единиц совокупности в каждой группе fi
Слайд 32
Структурные средние
применяются для изучения внутреннего строения рядов
распределения значений признака, а также для оценки средней величины
(степенного типа), если по имеющимся статистическим данным ее расчет не может быть выполнен.
Слайд 33
Структурные средние
Мода
наиболее часто повторяющееся значения признака
где ХMo - нижнее значение модального интервала;
mMo -
число наблюдений или объем взвешивающего признака в модальном интервале (в абсолютном либо относительном выражении);m Mo-1 - то же для интервала, предшествующего модальному;
m Mo+1 - то же для интервала, следующего за модальным;
h - величина интервала изменения признака в группах
Слайд 35
Модальный интервал величины стажа 6-8 лет,
а мода
продолжительности стажа:
Мо=6+2(35-20) / (35-20)+(35-11) = 6.77 года
Слайд 36
Структурные средние
Медиана
величина признака, которая делит упорядоченную
последовательность его значений на две равные по численности части
где XMe - нижняя граница медианного интервала;
hMe - его величина;
m2- половина от общего числа наблюдений или половина объема того показателя, который используется в качестве взвешивающего в формулах расчета средней величины;
SMe-1 - сумма наблюдений (или объема взвешивающего признака), накопленная до начала медианного интервала;
mMe - число наблюдений или объем взвешивающего признака в медианном интервале
Слайд 37
медиана
В дискретном ряду распределения медиана находится непосредственно по
накопленной частоте, соответствующей номеру медианы .
Слайд 38 Дискретный ряд - это такой вариационный ряд, в основу
построения которого положены признаки с прерывным изменением (дискретные признаки):
тарифный разряд, количество детей в семье, число работников на предприятии и т.д.Эти признаки могут принимать только конечное число определенных значений.
Слайд 39 Для варьирующего ряда ( т.е. построенного в порядке
возрастания, или убывания индивидуальных величин) с нечетным числом членов
медианой является варианта, расположенная в центре ряда.Если число членов четное – медиана = сред.арифмет.из двух смежных вариант.
