Слайд 2
Современный этап развития общества характеризуется широким внедрением статистики
в различные области науки, техники, народного хозяйства. Трудно назвать
область, где статистика не могла бы найти себе применения. Это в полной мере относится к медицине и здравоохранению.
Термин «статистика» (от лат. status – состояние, положение) впервые был применен при описании состояния государства в середине XVIII века. Как общественная наука статистика возникла в Англии в XVIII веке, хотя примитивные подсчеты производились уже в глубокой древности
Слайд 3
В настоящее время слово «статистика употребляется в трех
значениях.
Во-первых, под статистикой понимают общественную науку, которая изучает
количественную сторону общественных и массовых явлений в неразрывной связи с их качественной стороной.
Во-вторых, статистика включает в себя сбор цифровых, статистических данных, характеризующих то или другое общественное явление или процесс.
В-третьих, статистика – это сами цифры, характеризующие эти явления и процессы.
Слайд 4
Следовательно, статистическими данными являются те цифры, которые характеризуют
массовые явления, процессы, состояния.
Изучение статистических методов способствует развитию у
студентов и врачей критических взглядов, дедуктивных и индуктивных способностей
(дедукция – метод анализа, при котором из общих положений логический выводятся частные; индукция – метод анализа от частного к общему). Статистический анализ позволяет обосновать ту или иную тактику врача в предупреждении и лечении заболеваний.
Слайд 5
Статистика – это общественная наука, изучающая количественную сторону
общественных и массовых явлений в неразрывной связи с их
качественной стороной.
Статистика включает в себя сбор цифровых, статистических данных характеризующих то или другое общественное явление или процесс.
Характерной особенностью статистики является применение ее для изучения массовых, а не единичных явлений. По единичным наблюдениям невозможно выявить, вскрыть общие, типичные особенности изучаемого процесса. В массе же наблюдений статистика устанавливает наиболее общие закономерности, характерная для всей группы исследуемого явления.
Слайд 6
В медицинской статистике различают два основных раздела: статистику
здоровья населения и статистику здравоохранения. Статистика здоровья изучает здоровья
общества в целом и отдельных его групп и устанавливает зависимость здоровья от различных факторов социальной среды. Статистика здравоохранения анализирует данные о сети медицинских и санитарных учреждений, их деятельности и кадрах, оценивает эффективность различных мероприятий по профилактике и лечению болезней.
Слайд 7
Задачами
медицинской статистики являются:
- выявление особенностей состояния
здоровья населения и факторов, определяющих его;
- изучение данных о
сети, деятельности и кадрах лечебно-профилактических учреждений, а также данных о результатах лечебно-оздоровительных мероприятий;
- применение методов санитарной статистики в экспериментальных, клинических, гигиенических и лабораторных исследованиях.
Слайд 8
Работники здравоохранения должны уметь интерпретировать результаты лабораторных исследований,
клинических наблюдений и измерений, чтобы использовать их при рекомендациях
по профилактике и лечению различных заболеваний.
В то же время именно медицинские работники поставляют основную массу данных медицинской статистики, поэтому им необходимо знать, как эти данные могут и должны использоваться, чтобы не допускать неточности в регистрации демографических и медицинских событий.
Слайд 9
Статистика в медицине используется также для определения различных
норм (санитарно-гигиенического характера), расчет доз лекарственных препаратов, определения стандартов
физического развития, оценки эффективности примененных методов профилактики или лечения тех или иных заболеваний и т.д.
Статистический анализ позволяет обосновать ту или иную тактику врача в предупреждении или лечении заболеваний. Кроме того, огромный поток информации требует краткости изложения.
Статистика выполняет также информативную роль в медицине, является средством лучшего понимания других дисциплин.
Слайд 10
Изучение того или иного явления с применением статистического
метода требует от врача прежде всего умелого подхода к
выбору объекта исследования, так называемой статистической совокупности.
Статистической совокупностью называют группу, состоящую из множества относительно однородных элементов, взятых вместе в известных границах времени и пространства.
Статистическая совокупность и ее групповые свойства
Слайд 11
Статистическая совокупность состоит из отдельных единичных наблюдений. Численность
единиц наблюдения в совокупности определяет объем исследования и обозначается
буквой «n».
Каждый первичный элемент, составляющий статистическую совокупность и наделенный признаками сходства, принято называть единицей наблюдения (счетной единицей).
Слайд 12
Каждая единица наблюдения имеет несколько признаков, общих для
всех единиц, т.е. признаков сходства, позволяющих объединить все элементы
в единый объект наблюдения. Помимо признаков сходства каждая единица наблюдения обладает и множеством других признаков, часть из которых может стать предметом изучения, но учитываются только те из них, которые необходимы для достижения поставленной цели и решения конкретных задач исследования.
Эти признаки учитывают (регистрируют) и поэтому их называют учитываемыми.
Слайд 13
Признаки, по которым различаются элементы статистической совокупности, называют
учетными признаками
Т.О. учетными признаками, общими для сестринского персонала, -
признакам сходства – будут являться:
- профессия (медицинская сестра);
- место работы (конкретное лечебно-профилактическое учреждение).
Учетными признаками, по которым они различаются, являются:
- стаж работы по специальности или в данном медицинском учреждении;
- возраст и т.д.
Слайд 14
Такие учитываемые признаки как пол, возраст, место жительства,
сроки заболевания и госпитализации, результаты клинических исследований, исходы лечения
и другие позволяют всесторонне изучить не только каждый элемент совокупности (единицу наблюдения), но и всю совокупность в целом.
Слайд 15
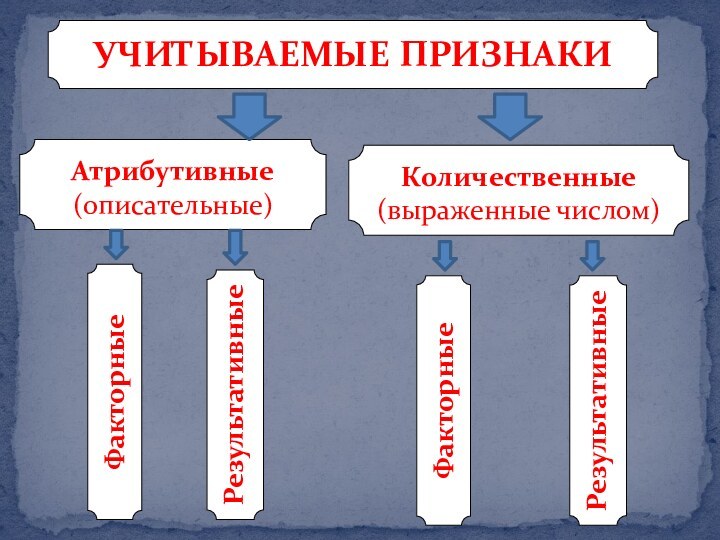
УЧИТЫВАЕМЫЕ ПРИЗНАКИ
Атрибутивные
(описательные)
Количественные
(выраженные числом)
Факторные
Результативные
Факторные
Результативные
Слайд 16
По характеру учетные признаки делятся на: атрибутивные (описательного
характера, выраженные словесно) и
количественные (выраженные числом).
К атрибутивным
признакам относятся: пол, профессия, нозологическая форма болезни, исход лечения, место жительства и пр.
К количественным признаком относятся: рост, масса тела, число дней лечения и т.д.
Каждая величина количественного признака называется вариантой и обозначается буквой «V».
Слайд 17
Факторными называются такие признаки, под влиянием которых изменяются
другие, зависящие от них результативные признаки.
С изменением величины
факторного признака происходит соответствующее возрастание или снижение числовых значений результативного признака.
Так, например, с увеличением возраста ребенка увеличивается его рост
(возраст - факторный признак,
рост – результативный признак).
Слайд 18
К факторным признакам следует отнести методы профилактики, пол,
возраст, профессию, доход и др.
К результативным – заболевание
(диагноз), его исход (выздоровление, смерть, инвалидность), массу тела, рост и др.
Слайд 19
Генеральная совокупность объектов
Выборка
(реально обследуемое множество
объектов из
генеральной совокупности
Статистическая совокупность носит название генеральной, если в ней
изучаются все составляющие элементы.
Выборочная совокупность это часть генеральной совокупности, отобранная специальным методом и предназначенная для характеристики генеральной совокупности
Слайд 20
Выборочный метод является основным при изучении статистической совокупности,
однако он должен дать такую информацию, которая позволила бы
судить о состоянии генеральной совокупности,
т.е. выборка должна быть достаточно представительной (репрезентативной). Репрезентативность обеспечивается определенными правилами выборки и расчетами.
Слайд 21
Для обеспечения репрезентативности выборочной совокупности к ней предъявляют
два основных требования:
а) она должна обладать основными характерными
чертами генеральной совокупности, т.е. быть максимально на нее похожей;
б) она должна быть достаточной по объему
(числу наблюдений), чтобы более точно выразить особенности генеральной совокупности.
Статистика располагает специальными формулами или же готовыми таблицами, по которым можно определить необходимое число наблюдений в выборочной совокупности.
Слайд 22
Основными величинами, которыми оперирует статистика, являются абсолютные и
относительные величины, отражающие качественную структуру статистической совокупности и характеризующие
распределение признаков (первое свойство статистической совокупности).
Абсолютные и относительные величины
Слайд 23
Абсолютные величины используют очень широко. Они несут важную
информацию о размере того или иного явления: количестве больных,
родившихся, числе коек в стационаре и т.д.
Однако при рассмотрении абсолютных величин чаще всего можно сделать только некоторые предварительные выводы и для дальнейшего анализа возникает необходимость в преобразовании этих величин в производные величины: относительные и средние.
Слайд 24
В городе «А» выявлено В 2010 г. 75
больных ревматоидным артритом (РА), а в городе «Б» за
этот период обнаружено 85 подобных случаев заболеваний. Можно ли сказать, что в городе «Б» выше уровень заболеваемости данной патологией?
Город «А» 25,0 %ооо
Город «Б»
Слайд 25
Относительные величины
(статистические коэффициенты), получаемые из соотношения
двух сравниваемых чисел, для удобства сопоставления обычно умножаются на
какое-либо круглое число (100, 1000, 10000, 100000), которые называются базой или основанием. Соответственно этому относительные величины могут быть выражены в -
(%), «промилле» (‰), «продецимилле» (‰о), «просантимилле» (%ооо) и т.д.
Слайд 26
Общая заболеваемость, рождаемость, смертность, младенческая смертность всегда выражается
в промилле (‰),
а заболеваемость с временной нетрудоспособностью рассчитывается
на 100 работающих, летальность, частота осложнений выражаются в %.
Слайд 27
Различают следующие виды относительных величин: интенсивные, экстенсивные показатели,
показатели соотношения и наглядности.
Интенсивные показатели характеризуют частоту (интенсивность, уровень,
распространенность) явления в среде, в которой оно происходит и с которой непосредственно органический связано, за определенный промежуток времени, чаще всего за год.
Экстенсивные показатели характеризуют распределения явления или среды на его составные части, его внутреннюю структуру или отношение частей к целому (удельный вес).
Слайд 28
Интенсивный показатель =Абсолютный размер явления * 1000
Абсолютный размер среды
При вычислении интенсивных показателей необходимо знание двух статистических совокупностей, одна из которых представляет среду, а вторая – явление. Среда продуцирует это явление. Средой может быть численность населения, количество работающих, новорожденных и т.д.
Слайд 29
Экстенсивный показатель =Часть явления *
1000
Явление в целом
В качестве примеров экстенсивных показателей применяемых в медицине и здравоохранении, можно назвать структуру заболеваемости населения; распределение госпитализированных больных по отдельным нозологическим формам и т.д.
Слайд 30
Пример: в 2010 г. в городе «Н» зарегистрировано
500 случаев заболеваний костно-мышечной системы, в том числе 75
случаев ревматоидного артрита (РА), 315 случаев остеоартроза, 130 системного поражения соединительной ткани,97 анкилозирующего спондилоартрита и т.д.
Экстенсивный показатель =
75 (РА – часть явления) 100 % = 15,0 %.
500 (БКМС – явление в целом)
Доля РА среди БКМС составляет 15%.
Слайд 31
Показатель соотношения характеризует отношение между двумя самостоятельными совокупностями
(в этом его сходство с интенсивным показателем), причем независимые
совокупности не только связаны друг с другом, но и не продуцируют одн
а другую (в этом отличие показателя соотношения от интенсивного коэффициента). Показателями соотношения являются показатели обеспеченности населения врачами, медсестрами, койками рассчитанные на 1000, 10000 населения. Их широко используют при планировании здравоохранения.