- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Сводка и группировкастатистическихданных
Содержание
- 2. 1. Понятие о статистической сводке. Программа и
- 3. Дальнейшая задача статистики: первичные
- 4. Статистическая сводка научно-организованная обработка материалов наблюдения, включающая
- 5. Различают простую и сложную сводкуПри простой сводке
- 6. Содержание сводки:Сводка состоит из следующих этапов: Выбор
- 7. План статистической сводкиСодержит указания о последовательности и
- 8. 2. Группировка как основа сводки. Задачи и
- 9. Основание группировкиПризнак, лежащий в основе группировки, называется
- 10. С помощью метода группировки решаются следующие задачи:выделение
- 11. Виды группировкиВ зависимости от решаемых задач различают типологические, структурные и аналитические группировки
- 12. Типологическая группировка Это разделение исследуемой совокупности на
- 13. Распределение предприятий и организаций РФ по
- 14. Структурная группировка Это группировка, в которой происходит
- 15. Распределение населения РФ по величине среднедушевых денежных
- 16. А.В.Сиденко Сводка и группировка
- 17. Аналитическая группировка позволяет выявить взаимосвязи между
- 18. Зависимость заработной платы от стажа Таблица 3
- 19. А.В.Сиденко Сводка и группировка
- 20. В зависимости от степени сложности массового явления
- 21. От группировок следует отличать классификацию. это систематизированное
- 22. Отличительные черты классификации:в ее основу кладется качественный
- 23. 3. Определение количества выделяемых групп Важнейшим
- 24. Если в основании группировки лежит количественный
- 25. Интервал группировки - это количественное значение, которое
- 26. Группировки с равными интервалами применяются в
- 27. Размер равного интервала Для группировок с
- 29. где: R – разность между максимальным и
- 30. Оптимальное количество групп определяется по формуле Стерджеса:
- 31. Пример 1Если изучаемая совокупность состоит из 50
- 32. Получаем следующее соотношение:Источник: результаты расчетов по формуле Стерджеса Таблица 4Определение количества групп по формуле Стерджеса
- 33. Интервалы групп могут быть открытые (указана одна
- 34. Ряды распределения Статистический ряд распределения представляет собой
- 35. Виды рядов распределенияВ зависимости от признака, положенного в основу образования ряда распределения, различают:
- 36. Атрибутивныминазывают ряды распределения, построенные по качественным признакам.
- 37. Вариационныминазываются ряды распределения, построенные по количественному признаку
- 38. Вариационный ряд распределения состоит из двух элементов:
- 39. Сумма всех частот равна численности всей совокупностиЧастости
- 40. В зависимости от характера вариации признака вариационные
- 41. Пример 2имеются результаты обследования 20 семей, в
- 42. Таблица 5Источник: рассчитано по примеру 2.Распределение 20 семей по количеству детей
- 43. Микроперепись населения России в 1994 г.Таблица 6Источник:
- 44. Полигон распределения
- 45. Распределение 30 рабочих бригад по размеру месячной заработной платыИсточник: Числа условныеТаблица 7
- 46. Гистограмма
- 47. Для графического изображения интервального вариационного ряда применяется
- 48. Гистограмма
- 49. В ряде случаев для графического изображения интервальных
- 50. Кумулята
- 51. Рассмотрим, как подсчитываются параметры кумуляты на примере
- 52. Накопленная частота последнего интервала должна быть равна
- 53. На практике приходится пользоваться уже имеющимися группировками,
- 54. 5. Вторичная группировкаВторичная группировка – это образование
- 55. Первый способ Второй способсостоит в укрупнении первоначальных
- 56. Имеется группировка сотрудников двух управлений
- 57. Приведенные данные не позволяют сравнить распределение работников
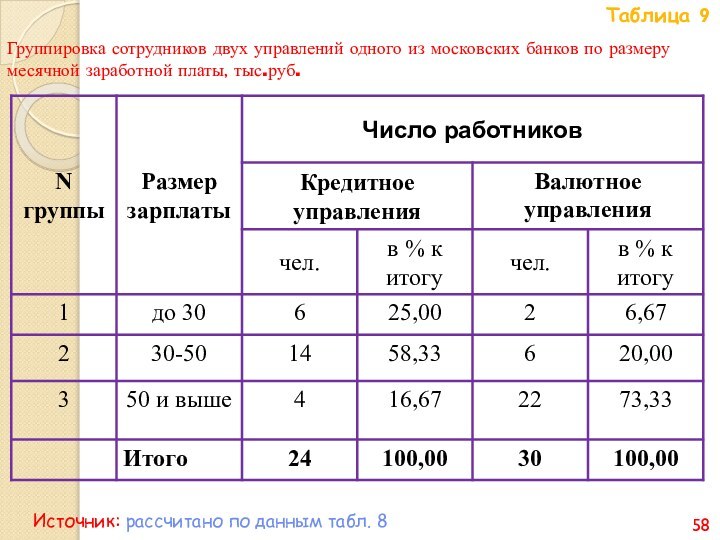
- 58. Таблица 9Группировка сотрудников двух управлений одного из
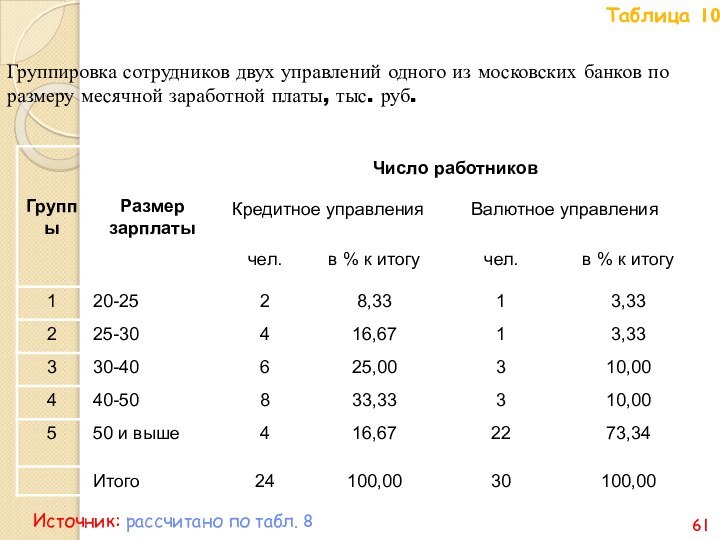
- 59. При вторичной группировке методом долевой перегруппировки устанавливаем
- 60. По валютному управлению производим перегруппировку следующим образом.
- 61. Скачать презентацию
- 62. Похожие презентации




















































Слайд 2 1. Понятие о статистической сводке. Программа и план
сводки
исследования. В результате проведения статистического наблюдения получают первичную информацию, характеризующую отдельные единицы изучаемой совокупностиСлайд 3 Дальнейшая задача статистики: первичные данные
систематизируются и с помощью обобщающих показателей дается сводная характеристика
всей совокупности
Слайд 4
Статистическая сводка
научно-организованная обработка материалов наблюдения, включающая подсчет
групповых и общих итогов, систематизацию, группировку данных, составление таблиц
Слайд 5
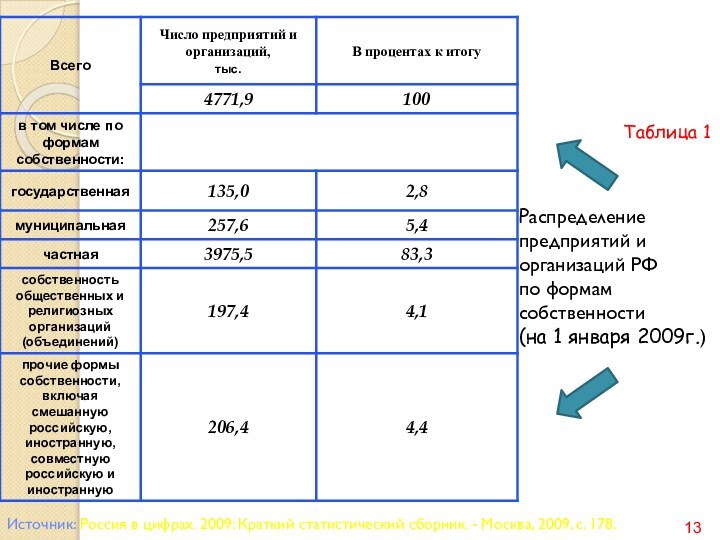
Различают простую и сложную сводку
При простой сводке производится
подсчет только общих итогов по изучаемой совокупности
При сложной сводке
производится: группировка единиц наблюдения; подсчет итогов по каждой группе и по всей совокупности; представление результатов группировки в виде статистических таблиц
Слайд 6
Содержание сводки:
Сводка состоит из следующих этапов:
Выбор группировочного
признака
Определение порядка формирования групп
Разработка системы статистических показателей
для характеристики отдельных групп и совокупности в целомРазработка макетов статистических таблиц для представления результатов сводки
Слайд 7
План статистической сводки
Содержит указания о последовательности и сроках
выполнения отдельных частей сводки, ее исполнителях, о порядке изложения
и представления результатовСлайд 8 2. Группировка как основа сводки. Задачи и виды
группировок
Группировка представляет собой метод, при котором вся исследуемая совокупность
разделяется на группы по какому-то существенному признаку
Слайд 9
Основание группировки
Признак, лежащий в основе группировки, называется группировочным
или основанием группировки
В зависимости от вида группировочных признаков различают
группировки по количественным и качественным (атрибутивным) признакам
Слайд 10
С помощью метода группировки решаются следующие задачи:
выделение социально-экономических
типов явлений
изучение структуры явления и структурных сдвигов, происходящих в
немвыявление связей и зависимостей между отдельными признаками явлений
Слайд 11
Виды группировки
В зависимости от решаемых задач различают типологические,
структурные и аналитические группировки
Слайд 12
Типологическая группировка
Это разделение исследуемой совокупности на однородные
группы, социально-экономические типы. Примером типологической группировки может служить группировка
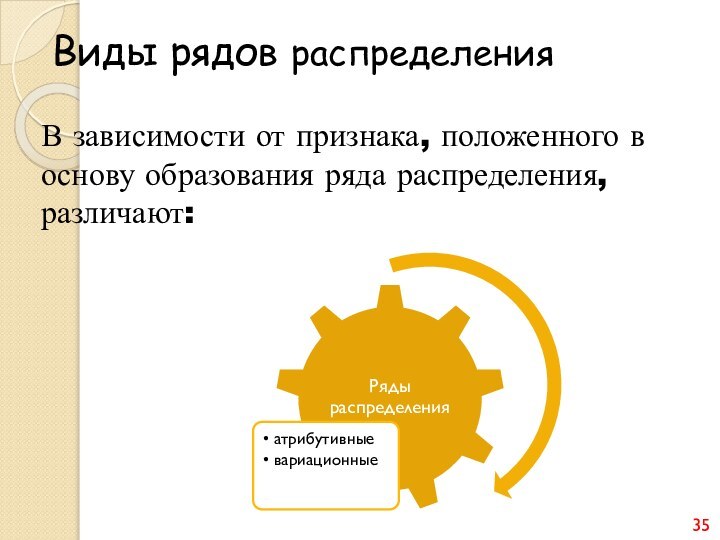
предприятий России по формам собственности в 2006 г.:Слайд 13 Распределение предприятий и организаций РФ по формам собственности (на
1 января 2009г.)
Источник: Россия в цифрах. 2009: Краткий статистический
сборник. - Москва, 2009, с. 178. Таблица 1
Слайд 14
Структурная группировка
Это группировка, в которой происходит разделение
однородной совокупности на группы, характеризующие ее структуру по какому-то
варьирующему признаку.Примером структурной группировки может служить группировка населения России по размеру среднедушевого денежного дохода в 2007 г.:
Слайд 15 Распределение населения РФ по величине среднедушевых денежных доходов
в 2007 году
(в процентах к итогу)
Источник: Россия в
цифрах. 2008: Краткий статистический сборник. - Москва, 2008, с. 125Таблица 2
Слайд 17
Аналитическая группировка
позволяет выявить взаимосвязи между изучаемыми
явлениями и их признаками. Примером аналитической группировки может служить
– зависимость средней заработной зарплаты от стажа работы:Слайд 20 В зависимости от степени сложности массового явления и
задач анализа группировки могут производиться по одному или нескольким
признакамГруппировка по одному признаку называется простой. Группировка по двум и более признакам называется сложной (комбинационной)
Слайд 21
От группировок следует отличать классификацию.
это систематизированное распределение
явлений и объектов на определенные группы, классы, разряды с
учетом их сходства и различияКлассификация –
Слайд 22
Отличительные черты классификации:
в ее основу кладется качественный признак
классификации
стандартны. Они устанавливаются органами государственной и международной статистики
классификации устойчивы.
Они остаются неизменными в течение длительного времени
Слайд 23
3. Определение количества выделяемых групп
Важнейшим вопросом
является определение количества выделяемых групп.
Если в основании
группировки лежит атрибутивный признак, то количество выделяемых групп определяется самим этим признаком. Например, производя группировку студентов, посещающих бассейн, по полу, выделяют две группы: мужчин и женщинСлайд 24 Если в основании группировки лежит количественный признак,
то производят специальные расчеты для определения количества групп и
величин интервалов группировки
Слайд 25
Интервал группировки -
это количественное значение, которое определяется
как разность между максимальным и минимальным значениями признака в
каждой группеИнтервалы группировки могут быть:
Равные
Неравные
Слайд 26
Группировки с равными интервалами
применяются в тех
случаях, когда вариация признака проявляется в сравнительно узких границах
и распределение является практически равномерным
Слайд 27
Размер равного интервала
Для группировок с
равными интервалами величина интервала h определяется как отношение разности
между максимальным и минимальным значениями признака к количеству выделяемых групп:
Слайд 29
где:
R – разность между максимальным и минимальным
значениями признака (размах вариации)
Xmax – максимальное значение признака в
совокупностиXmin – минимальное значение признака в совокупности
n – количество выделяемых групп
Слайд 30
Оптимальное количество групп определяется по формуле Стерджеса:
n = 1 + 3,322lgN,
где:
n –
количество образуемых групп;N – число единиц совокупности
Слайд 31
Пример 1
Если изучаемая совокупность состоит из 50 единиц,
то число образуемых групп равно 7
n = 1 + 3,322lg50 = 7Расчеты по формуле Стерджеса
Слайд 32
Получаем следующее соотношение:
Источник: результаты расчетов по формуле Стерджеса
Таблица 4
Определение количества групп по формуле Стерджеса
Слайд 33 Интервалы групп могут быть открытые (указана одна из
границ) и закрытые (указаны и верхняя и нижняя граница
интервала). Величина открытого интервала приравнивается к величине смежного с ним интервалаПосле определения группировочного признака, количества групп и интервалов группировки данные сводки и группировки представляются в виде рядов распределения и оформляются в виде таблиц
Слайд 34
Ряды распределения
Статистический ряд распределения представляет собой упорядоченное
распределение единиц изучаемой совокупности на группы по определенному варьирующему
признаку
Слайд 35
Виды рядов распределения
В зависимости от признака, положенного в
основу образования ряда распределения, различают:
Слайд 36
Атрибутивными
называют ряды распределения, построенные по качественным признакам. Примерами
атрибутивного распределения может служить распределение населения по полу, национальности,
месту проживания
Слайд 37
Вариационными
называются ряды распределения, построенные по количественному признаку (в
порядке возрастания или убывания признака)
пример:
Распределение студентов по возрасту, росту
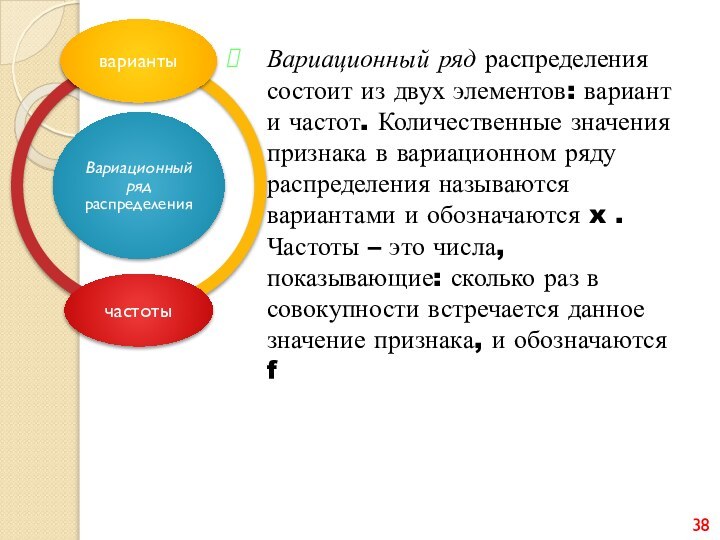
Слайд 38 Вариационный ряд распределения состоит из двух элементов: вариант
и частот. Количественные значения признака в вариационном ряду распределения
называются вариантами и обозначаются x . Частоты – это числа, показывающие: сколько раз в совокупности встречается данное значение признака, и обозначаются f
Слайд 39
Сумма всех частот равна численности всей совокупности
Частости –
это
частоты, выраженные в процентах к итогу или в долях.
Сумма всех частостей, выраженных в процентах, равна 100 %, в долях – 1Слайд 40 В зависимости от характера вариации признака вариационные ряды
распределения подразделяются на дискретные и интервальные
Если варианты признаков представлены
в виде целых чисел (например, число детей в семье), то такой вариационный ряд называется дискретнымКогда значения признака выражены в виде интервалов, это интервальный ряд
Вариационные ряды распределения представляют в виде таблицы, состоящей из двух колонок. В первой колонке приводятся отдельные значения варьирующего признака, т.е. варианты. Во второй – числа, показывающие, сколько раз в совокупности встречается данная варианта, т.е. частоты
Слайд 41
Пример 2
имеются результаты обследования 20 семей, в которых
выяснялось количество детей:
0 1 2 3 1 2 3
4 1 0 1 2 1 1 0 3 1 2 1 4 Поскольку значения признака представлены в виде целых чисел, построим дискретный ряд распределения
Слайд 43
Микроперепись населения России в 1994 г.
Таблица 6
Источник: статистической
информации - краткий статистический сборник
"Россия в цифрах",
Госкомстат, М., 1998.Для графического изображения дискретного вариационного ряда применяется полигон распределения
В качестве интервального вариационного ряда рассмотрим распределение 30 рабочих бригад по размеру зарплаты (см. пример 3)
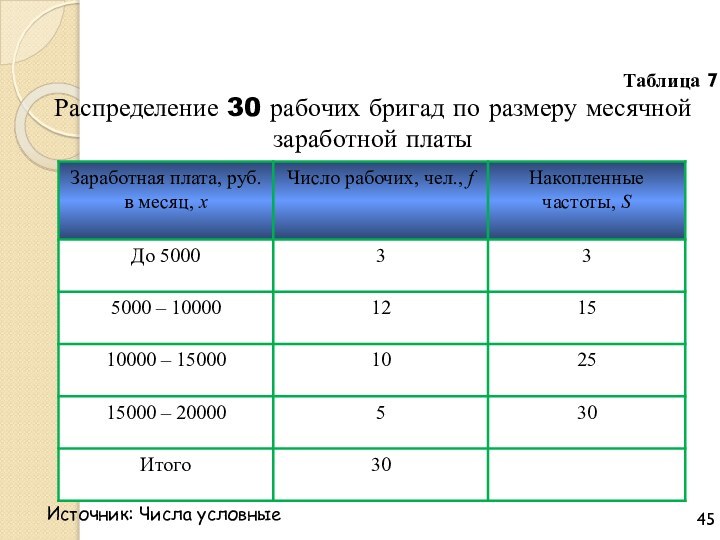
Слайд 45 Распределение 30 рабочих бригад по размеру месячной заработной
платы
Источник: Числа условные
Таблица 7
Слайд 47
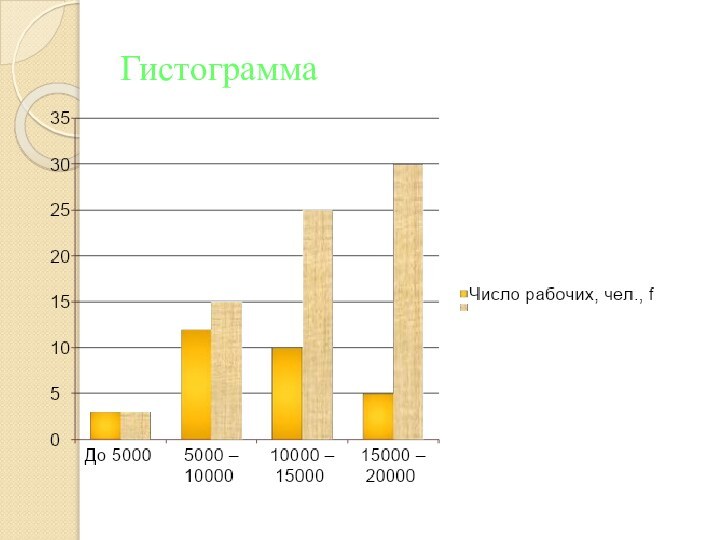
Для графического изображения интервального вариационного ряда применяется гистограмма
Любую
гистограмму можно преобразовать в полигон распределения. Для этого достаточно
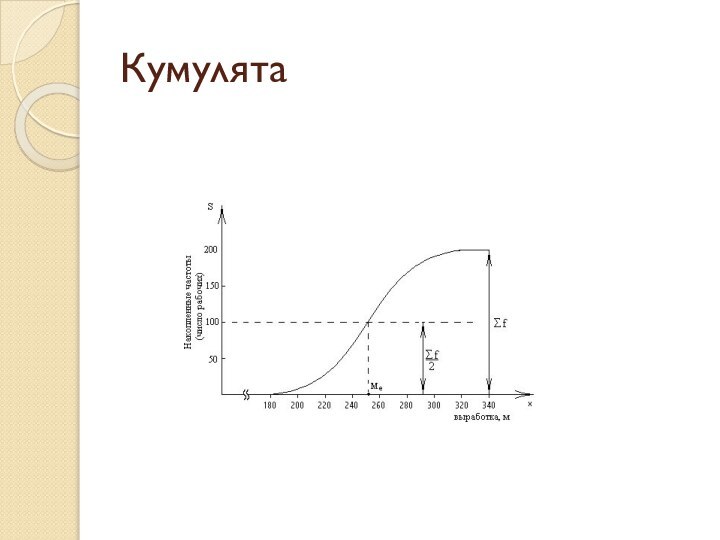
последовательно соединить середины верхних оснований образованных прямоугольниковСлайд 49 В ряде случаев для графического изображения интервальных вариационных
рядов применяется кумулята. Для ее построения сначала необходимо рассчитать
накопленные частоты. Они определяются путем последовательного суммирования частот предшествующих интервалов и обозначаются S. Накопленные частоты показывают, сколько единиц совокупности имеют значение признака не больше, чем рассматриваемое. Рассчитаем частоты для примера 3Слайд 51 Рассмотрим, как подсчитываются параметры кумуляты на примере таблицы
7 о распределении 30 рабочих по размеру заработной платы.
Для
первого интервала накопленная частота равна 3 (так как предшествующего интервала нет, 3 + 0 = 3), для второго интервала – 15 (3 + 12 = 15), для третьего – 25 (3 + 12 + 10 = 25 или 15 + 10 = 25), для последнего интервала накопленная частота равна 30 (3 + 12 + 10 + 5 = 30 или 25 + 5 = 30) Слайд 52 Накопленная частота последнего интервала должна быть равна сумме
частот, т.е. численности единиц совокупности. При построении кумуляты нижней
границе первого интервала присваивается накопленная частота, равная 0, и вся накопленная частота интервала присваивается его верхней границе. Для построения кумуляты на оси абцисс откладывают отрезки, соответствующие интервалам значений признака, на оси ординат – накопленные частотаСлайд 53 На практике приходится пользоваться уже имеющимися группировками, которые
могут быть несопоставимы из-за неодинаковых границ интервалов или различного
количества выделяемых групп. Для приведения таких группировок к сопоставимому виду используется метод вторичной группировки
Слайд 54
5. Вторичная группировка
Вторичная группировка – это образование новых
групп на основе ранее произведенной группировки. Применяют два способа
образования новых групп на основе ранее произведенной группировки
Слайд 55
Первый способ
Второй способ
состоит в укрупнении первоначальных интервалов.
Это наиболее простой и распространенный способ
называется методом долевой перегруппировки
и состоит в том, что за каждой группой закрепляется определенная доля единиц совокупности. Рассмотрим два способа на примереСлайд 56 Имеется группировка сотрудников двух управлений одного
из московских банков по размеру месячной заработной платы тыс.
руб.Источник: условные данные
Таблица 8
Слайд 57 Приведенные данные не позволяют сравнить распределение работников по
размеру месячной заработной платы, так как величины интервалов различны,
поэтому необходимо привести эти ряды распределения к сопоставимому виду.Произведем вторичную группировку, образовав группы с новыми укрупненными интервалами








![Автоматизация звука [Ш].](/img/tmb/6/521344/44660bcd5a7278376160aec37c8cc869-210x.jpg)