- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Тема 2. Парная линейная регрессионная модель
Содержание
- 2. Две переменные X и Y
- 3. Функциональная зависимость
- 4. Независимость
- 5. Статистическая зависимостьЕсли при изменении X меняется закон
- 6. Статистическая зависимостьЗдесь будет красивый рисунок (когда-нибудь)
- 7. Статистическая зависимостьСтатистическая зависимость называется корреляционной, если при
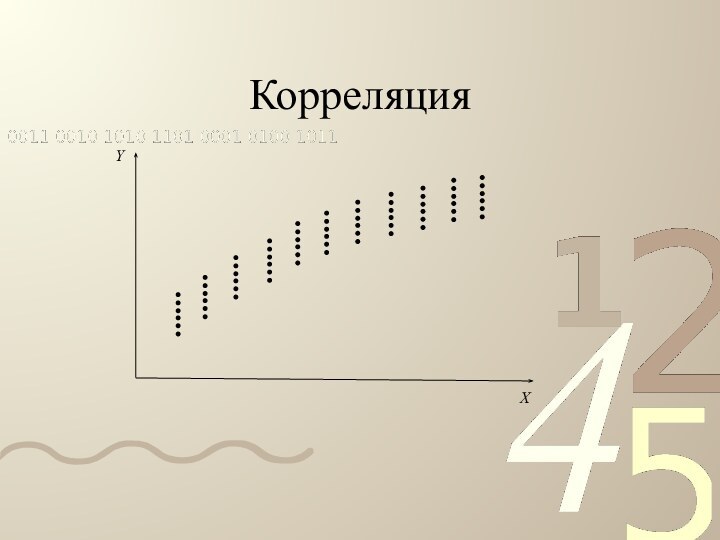
- 8. Корреляция
- 9. Корреляция
- 10. Гетероскедастичность
- 11. Гетероскедастичность
- 12. Корреляция и гетероскедастичность
- 13. Корреляция и гетероскедастичность
- 14. Корреляционная зависимостьЕсли каждому значению величины X соответствует
- 15. Случайная составляющаяОтклонение переменной Y от математического ожидания
- 16. Регрессионное уравнениеУравнениеназывается уравнением регрессии переменной Y на переменную X
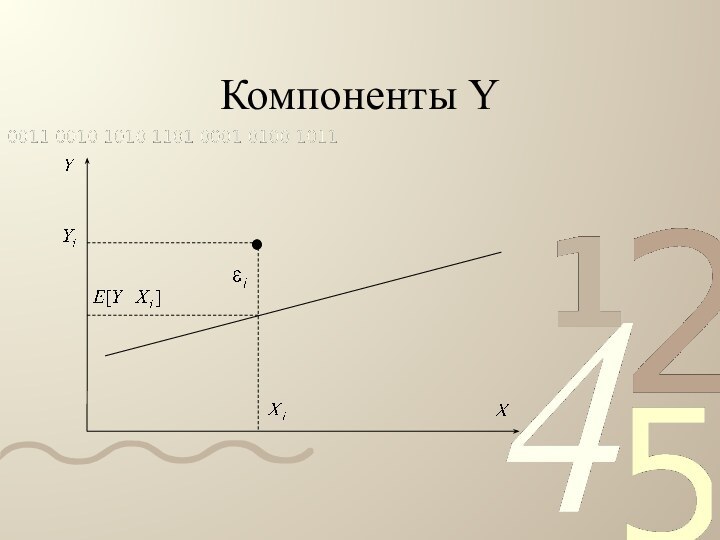
- 17. Компоненты Y
- 18. Экономический смысл невключение объясняющих переменных в уравнение.
- 19. Экономический смысл (продолжение)Неправильная функциональная спецификация. Функциональное
- 20. Способы определения регрессионной функции f(X) параметрический –
- 21. Выбор вида f(X)экономическая теорияопыт, интуиция исследователяэмпирический анализ данных
- 22. Эмпирический анализ данныхВ парном случае материал наблюдений представляет собой набор пар чисел: .
- 23. На плоскости каждому такому наблюдению соответствует точка:Полученный
- 24. Линейная Y=+X+.
- 25. Квадратичная
- 26. Показательная
- 27. Степенная
- 28. Гиперболическая
- 29. X и Y независимы
- 30. Парная линейная регрессионная модель Y=+X+.
- 31. Выбор коэффициентов регрессионной прямойИз всех возможных прямых
- 32. Выбор коэффициентов регрессионной прямойβ – коэффициент наклона (slope),α – свободный коэффициент (intercept)
- 33. Истинная линия регрессии, определяемая коэффициентами α и β
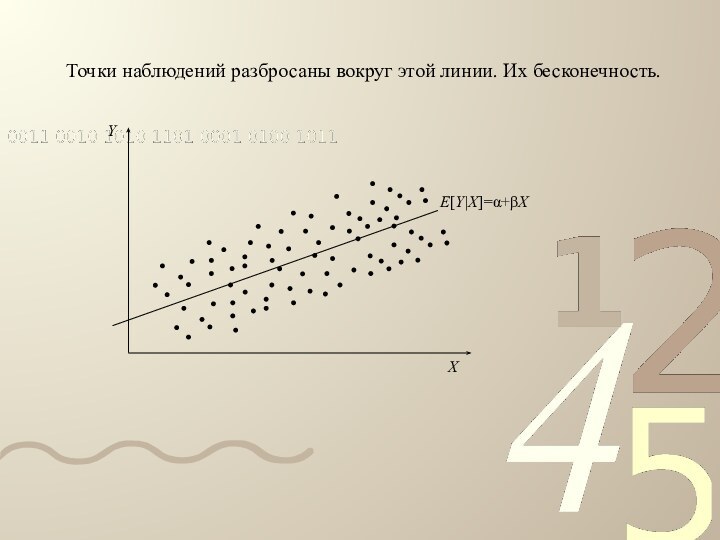
- 34. Точки наблюдений разбросаны вокруг этой линии. Их бесконечность.
- 35. В выборку попадает только их часть
- 36. В выборку попадает только их часть
- 37. И что мы наблюдаем Всего мы наблюдаем N точек
- 38. Линия, которую мы проводим
- 39. Линия, которую мы проводимПроводим прямую через центр
- 40. Реальные и прогнозные значения
- 41. Разницу между реальным и прогнозным значением назовем остатком
- 42. Рассмотрение остатков на графике
- 43. Истинная и оцененная линия регрессииМы надеемся, что
- 44. Грусть печальМетод наименьших квадратов не всегда состоятельный
- 45. Как найти «наилучшую» прямую аналитически?Выберем меру близости
- 46. Мера близости одной точки к прямой – остаток.
- 47. Интегральная мера близости
- 48. Интегральная мера близостипочему бы не минимизировать просто сумму остатков?
- 49. Для какой прямой сумма остатков равна 0?
- 50. для такой
- 51. и для такой
- 52. Метод наименьших квадратовСреди всех возможных прямых выбираем ту, для которой сумма квадратов остатков минимальна
- 53. Минимизация или
- 54. Система нормальных уравнений
- 55. МНК-коэффициенты ПЛРМ- коэффициент наклона- свободный коэффициент
- 56. Другие формы записи коэффициента наклона
- 57. ЗамечанияЛиния регрессии проходит через точку Мы предполагаем,
- 58. Теснота линейной корреляционной связиВ качестве меры близости
- 59. Вспомним теоретический коэффициент корреляции
- 60. Связь между коэффициентом корреляции и коэффициентом наклонаЗнак коэффициента наклона линии регрессии и коэффициента корреляции совпадают
- 61. Положительная корреляцияС ростом переменной X переменная Y в среднем растет (имеет тенденцию к росту)
- 62. Отрицательная корреляцияС ростом переменной X переменная Y в среднем убывает (имеет тенденцию к уменьшению)
- 63. Свойства коэффициента корреляции
- 64. Свойства коэффициента корреляции (продолжение)переменные не связаны линейной
- 65. Уравнение одно, коэффициенты корреляции разные
- 66. Скачать презентацию
- 67. Похожие презентации
Две переменные X и Y































































Слайд 7
Статистическая зависимость
Статистическая зависимость называется корреляционной, если при изменении
X меняется математическое ожидание случайной величины Y.
Если при
изменении переменной X меняется дисперсия переменной Y, такую зависимость называют гетероскедастичностью.Корреляция и гетерокедастичность могут наблюдаться одновременно
Слайд 14
Корреляционная зависимость
Если каждому значению величины X соответствует свое
значение
то говорят, что существует
регрессионная функция
Линию, которую описывает регрессионная функция, называется линия регрессии
Слайд 15
Случайная составляющая
Отклонение переменной Y от математического ожидания для
соответствующего значения переменной X называется ошибкой и обозначается
Слайд 18
Экономический смысл
невключение объясняющих переменных в уравнение. На
самом деле на переменную Y влияет не только переменная
X, но и ряд других переменных, которые не учтены в нашей модели по следующим причинам:мы знаем, что другая переменная влияет, но не модем ее учесть, потому как не знаем, как измерить (психологический фактор, например);
существуют факторы, которые мы знаем, как измерить, но влияние их на Y так слабо, что их не стоит учитывать;
существенные переменные, но из-за отсутствия опыта или знаний мы их таковыми не считаем.
Слайд 19
Экономический смысл (продолжение)
Неправильная функциональная спецификация. Функциональное соотношение
между Y и Х может быть определено неправильно. Например,
мы предположили линейную зависимость, а она может быть более сложной.Ошибки наблюдений (занижение реального уровня доходов). В этом случае наблюдаемые значения не будут соответствовать точному соотношению, и существующее расхождение будет вносить свой вклад в остаточный член.





























