Презентация на тему Угловая скорость и угловое ускорение

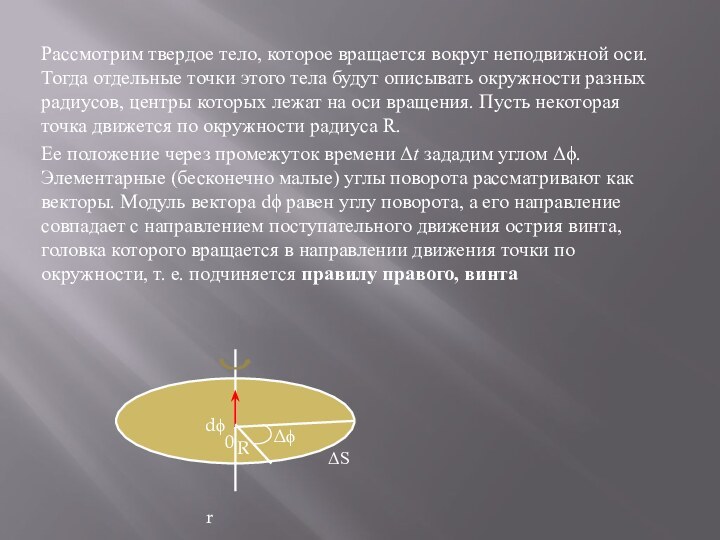
Тогда отдельные точки этого тела будут описывать окружности разных

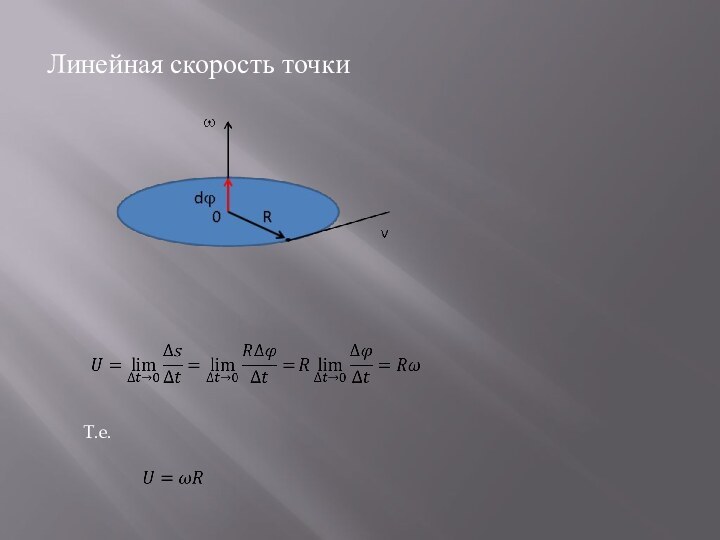
радиусов, центры которых лежат на оси вращения. Пусть некоторая точка движется по окружности радиуса R.
Ее положение через промежуток времени t зададим углом . Элементарные (бесконечно малые) углы поворота рассматривают как векторы. Мо­дуль вектора d равен углу поворота, а его направление совпадает с направле­нием поступательного движения острия винта, головка которого вращается в на­правлении движения точки по окружности, т. е. подчиняется правилу правого, винта

d

0



r

R

S

угла поворота тела по времени:

характеризовать перио­дом вращения Т — временем, за которое точка

совершает один полный оборот, т. е. поворачивается на угол 2. Так как промежутку времени t=T соответствует =2, то = 2/Т, откуда

T=2/

его движении по окружности, в единицу времени
n=1/T=/(2)
откуда
=2n

скорости по времени:

ускорения направлен вдоль оси вращения в сторону вектора элементарного

приращения угловой ско­рости.

по дуге окружности радиуса R, линейная ско­рость v, тангенциальное

ускорение а, нор­мальное ускорение аn) и угловыми величи­нами (угол поворота , угловая скорость (о, угловое ускорение ) выражается сле­дующими формулами:

s=R

v=R

а=R

0 — начальная угловая скорость.