- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теорема о пропорциональных отрезках.
Содержание
- 4. И тогда.Отрезки, образовавшиеся на одной стороне угла, пропорциональны соответствующим отрезкам, образовавшимся на другой стороне угла.
- 5. Вставьте пропущенные слова.Если … прямые пересекают стороны
- 6. Если параллельные прямые пересекают стороны угла, то,…
- 7. Верно лиЕсли перпендикулярные прямые пересекают стороны угла,
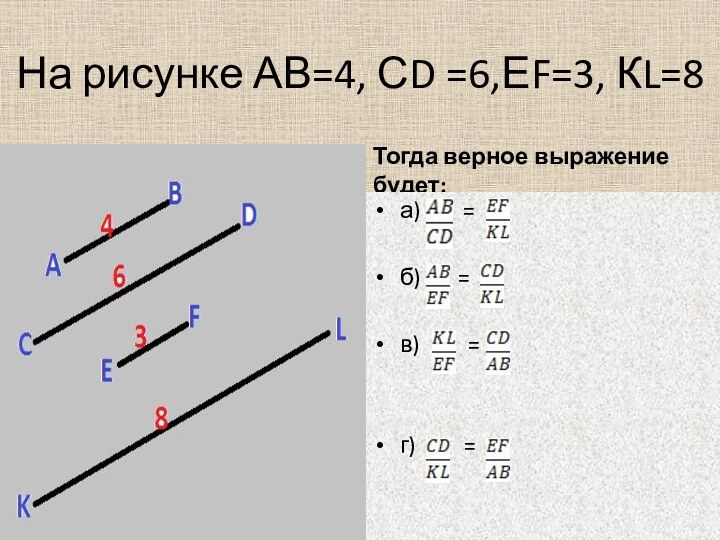
- 8. На рисунке АВ=4, СD =6,ЕF=3, КL=8Тогда верное
- 10. Решите следующие номера.№ 379, №388, № 398,
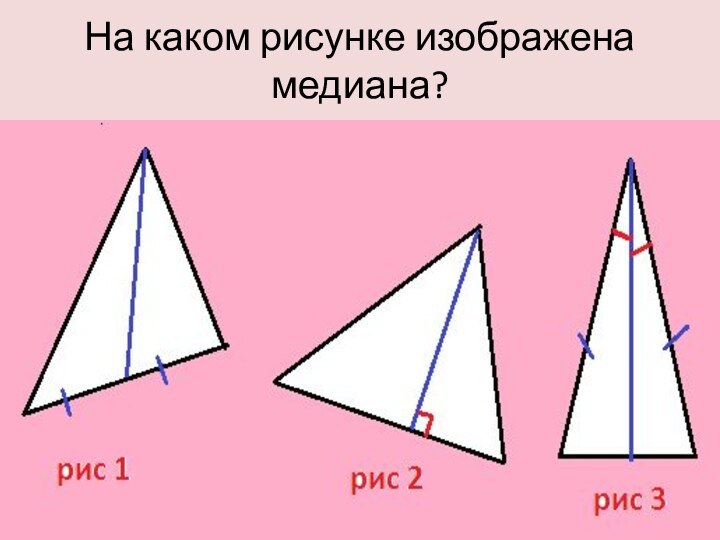
- 11. На каком рисунке изображена медиана?
- 12. Давайте вспомним, что же называется медианой?Определение: Медиана
- 13. Выполните следующие задания.1. Постройте треугольник АВС;2. Проведите
- 14. 7. Измерьте расстояние от другой вершины до
- 15. Делаем выводТри медианы треугольника пересекаются в одной
- 16. Основное свойство.Три медианы треугольника пересекаются в одной
- 17. Вставьте пропущенные слова.Три медианы треугольника пересекаются в
- 18. Верно лиТри медианы треугольника пересекаются в двух
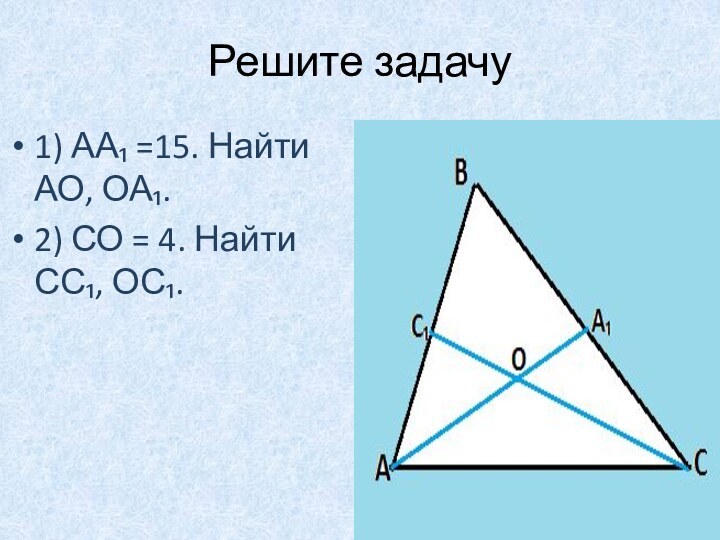
- 19. Решите задачу1) АА₁ =15. Найти АО, ОА₁.2) СО = 4. Найти СС₁, ОС₁.
- 20. Три медианы треугольника пересекаются в одной точке,
- 21. Решите задачи.№383, №390, №400
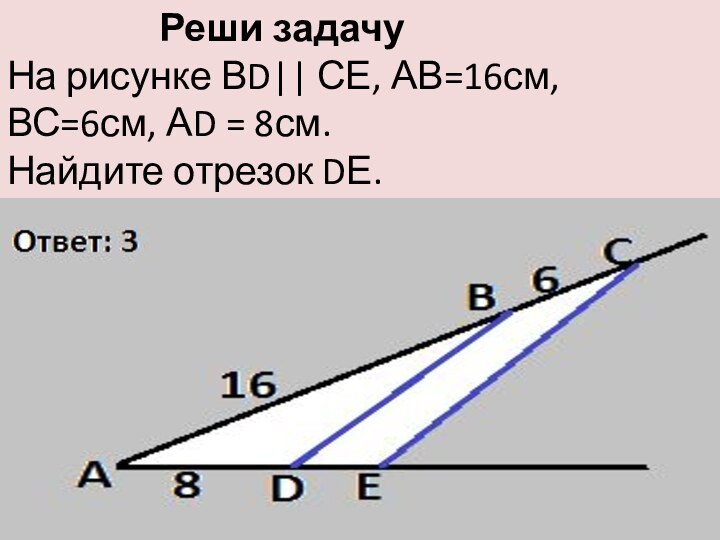
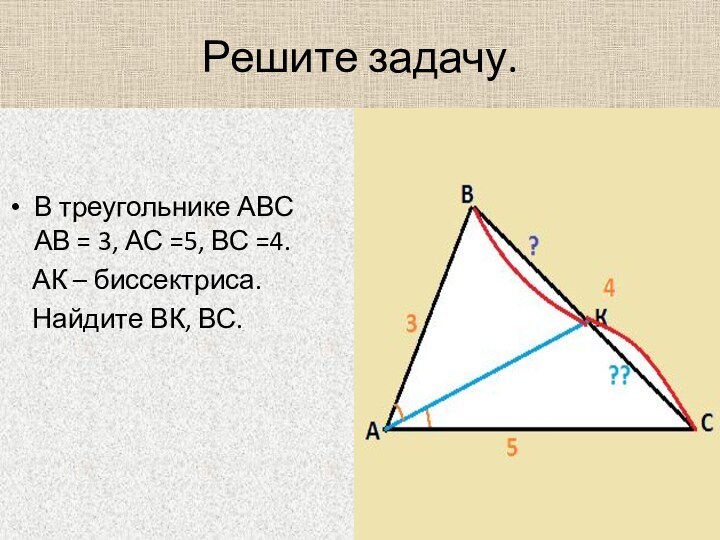
- 22. Решите задачу.В треугольнике АВС
- 23. Свойство биссектрисы треугольника.Биссектриса треугольника делит сторону на
- 24. ВЕРНО ЛИ:АК прилежит к ВС
- 25. Вставь пропуски:… треугольника делит сторону на отрезки
- 26. Теорема: Биссектриса треугольника делит сторону на отрезки
- 27. Решите задачи.№385,№401,№404,№405,№407,№409
- 28. Скачать презентацию
- 29. Похожие презентации
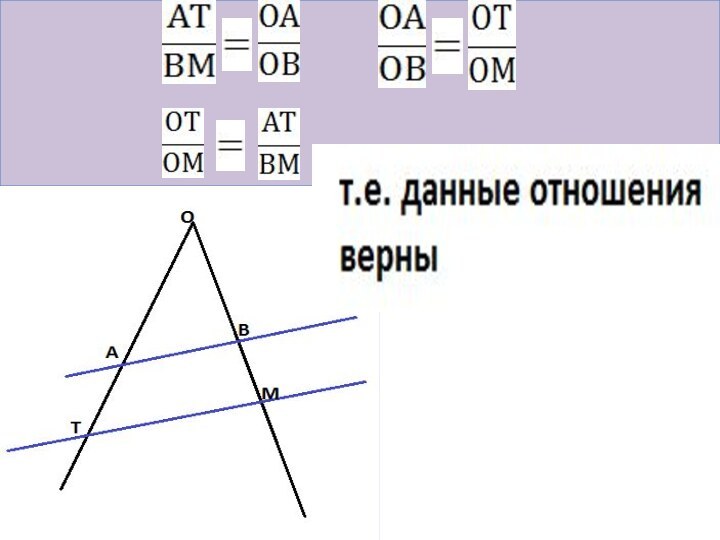
Итак. Что необходимо? 1)Угол. 2)Прямые













Слайд 4
И тогда.
Отрезки, образовавшиеся на одной стороне угла, пропорциональны
соответствующим отрезкам, образовавшимся на другой стороне угла.
Слайд 5
Вставьте пропущенные слова.
Если … прямые пересекают стороны угла,
то отрезки, образовавшиеся на одной стороне угла, пропорциональны соответствующим
отрезкам, образовавшимся на другой стороне угла.Если … прямые … стороны угла, то отрезки, образовавшиеся на одной стороне угла, пропорциональны соответствующим отрезкам, образовавшимся на другой стороне угла.
Слайд 6
Если параллельные прямые пересекают стороны угла, то,… образовавшиеся
на одной стороне угла, … соответствующим отрезкам, образовавшимся на
другой стороне угла.Если параллельные прямые пересекают стороны угла, то отрезки, … на одной стороне угла, пропорциональны соответствующим …, образовавшимся на другой стороне … .
Слайд 7
Верно ли
Если перпендикулярные прямые пересекают стороны угла, то
отрезки, образовавшиеся на одной стороне угла, пропорциональны соответствующим отрезкам,
образовавшимся на другой стороне угла.Если параллельные прямые пересекают стороны угла, то отрезки, образовавшиеся на одной стороне угла, равны соответствующим отрезкам, образовавшимся на другой стороне угла.
Слайд 12
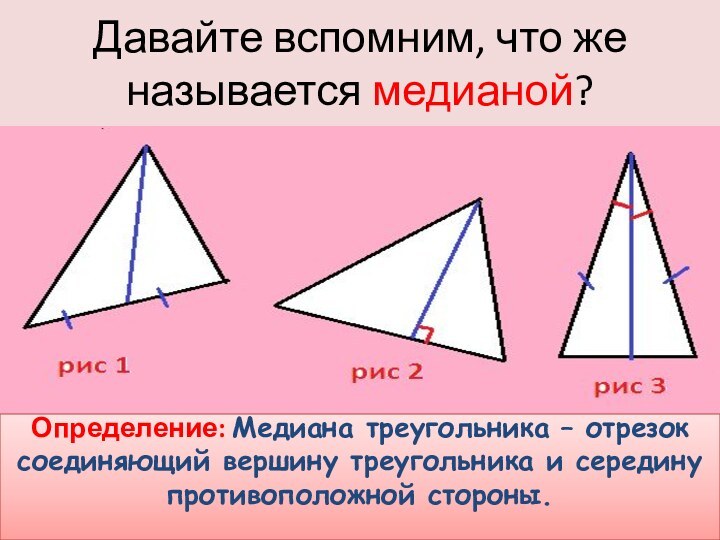
Давайте вспомним, что же называется медианой?
Определение: Медиана треугольника
– отрезок соединяющий вершину треугольника и середину противоположной стороны.
Слайд 13
Выполните следующие задания.
1. Постройте треугольник АВС;
2. Проведите любые
две медианы;
3. Точку пересечения обозначьте за О;
4. Измерьте расстояние
от вершины до т.О, запишите ответ a = … ;5. Измерьте оставшуюся часть отрезка, запишите ответ b = …;
6. Найдите отношение
Слайд 14 7. Измерьте расстояние от другой вершины до т.О,
запишите ответ c = … ;
8. Измерьте оставшуюся часть
отрезка, запишите ответ d = …;9. Найдите отношение
10. Что вы скажите про полученные отношения;
11. Как вы думаете в каком отношении т.О разделила медианы?
Слайд 15
Делаем вывод
Три медианы треугольника пересекаются в одной точке,
которая делит каждую из них в отношении 2:1, считая
от вершины треугольника.Точка в которой пересекаются медианы называется центроидом или
центром тяжести треугольника.
Слайд 16
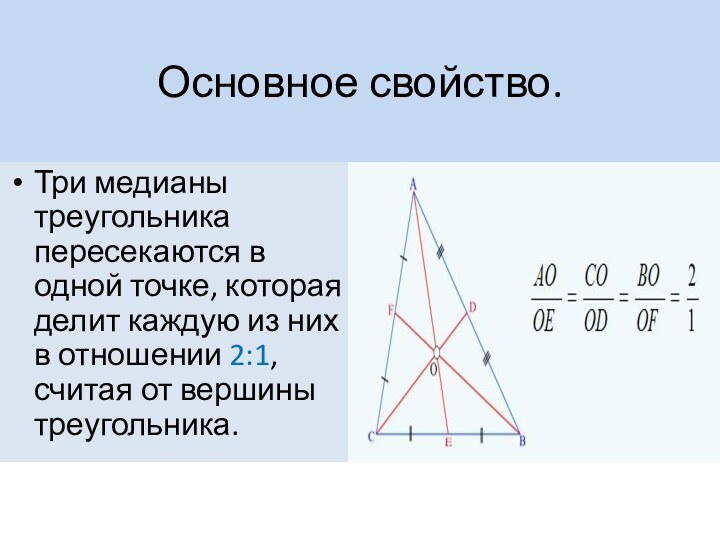
Основное свойство.
Три медианы треугольника пересекаются в одной точке,
которая делит каждую из них в отношении 2:1, считая
от вершины треугольника.
Слайд 17
Вставьте пропущенные слова.
Три медианы треугольника пересекаются в …
точке, которая делит каждую из них в отношении 2:1,
считая от вершины треугольника.Три медианы треугольника пересекаются в одной точке, которая … каждую из них в отношении 2:1, считая от вершины треугольника.
Три медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от … треугольника.
Три медианы треугольника пересекаются в одной точке, которая делит каждую из них в … , считая от вершины треугольника.
Слайд 18
Верно ли
Три медианы треугольника пересекаются в двух точках,
которая делит каждую из них в отношении 2:1, считая
от вершины треугольника.Три медианы треугольника пересекаются в одной точке, которая делит две из них в отношении 2:1, считая от вершины треугольника.
Три медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 1:2, считая от вершины треугольника.
Три медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины треугольника.
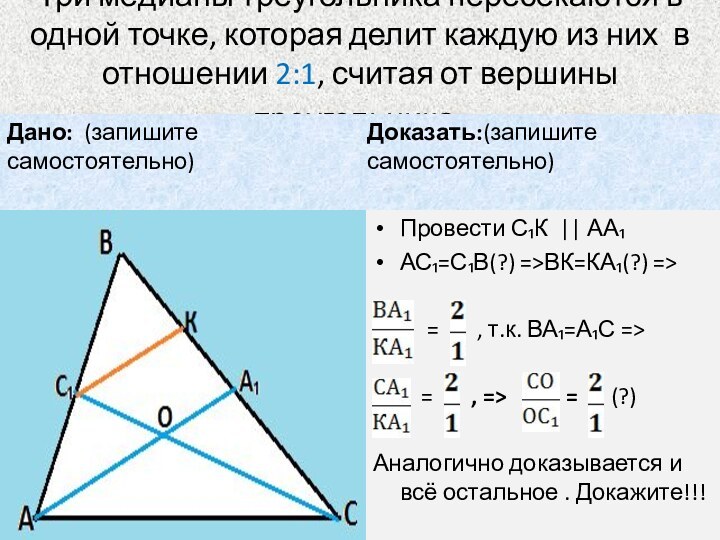
Слайд 20 Три медианы треугольника пересекаются в одной точке, которая
делит каждую из них в отношении 2:1, считая от
вершины треугольника.Дано: (запишите самостоятельно)
Доказать:(запишите самостоятельно)
Провести С₁К || АА₁
АС₁=С₁В(?) =>ВК=КА₁(?) =>
= , т.к. ВА₁=А₁С =>
= , => = (?)
Аналогично доказывается и всё остальное . Докажите!!!
Слайд 23
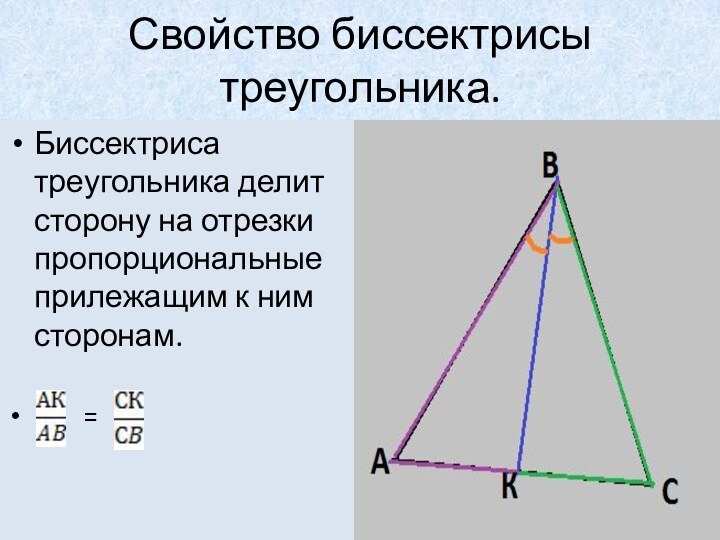
Свойство биссектрисы треугольника.
Биссектриса треугольника делит сторону на отрезки
пропорциональные прилежащим к ним сторонам.
=
Слайд 24
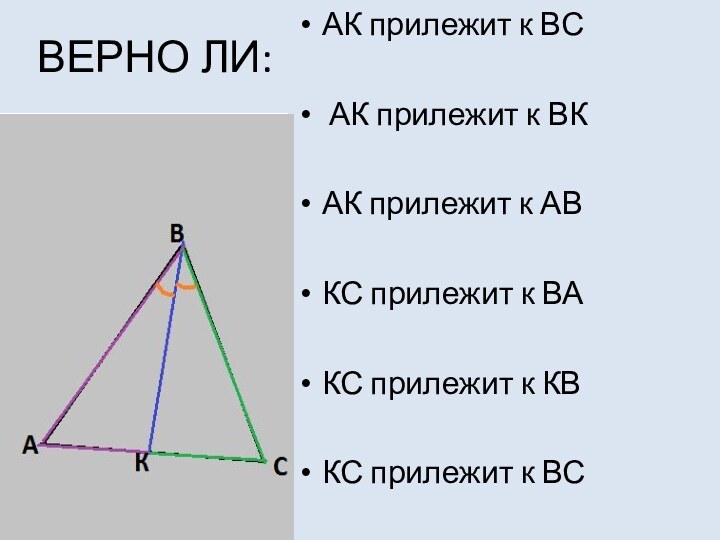
ВЕРНО ЛИ:
АК прилежит к ВС
АК
прилежит к ВК
АК прилежит к АВ
КС прилежит к ВА
КС
прилежит к КВКС прилежит к ВС
Слайд 25
Вставь пропуски:
… треугольника делит сторону на отрезки пропорциональные
прилежащим к ним сторонам.
Биссектриса треугольника делит сторону на отрезки
пропорциональные … к ним сторонам.Биссектриса треугольника делит сторону на отрезки … прилежащим к ним сторонам.
Биссектриса треугольника … сторону на отрезки пропорциональные прилежащим к ним сторонам.
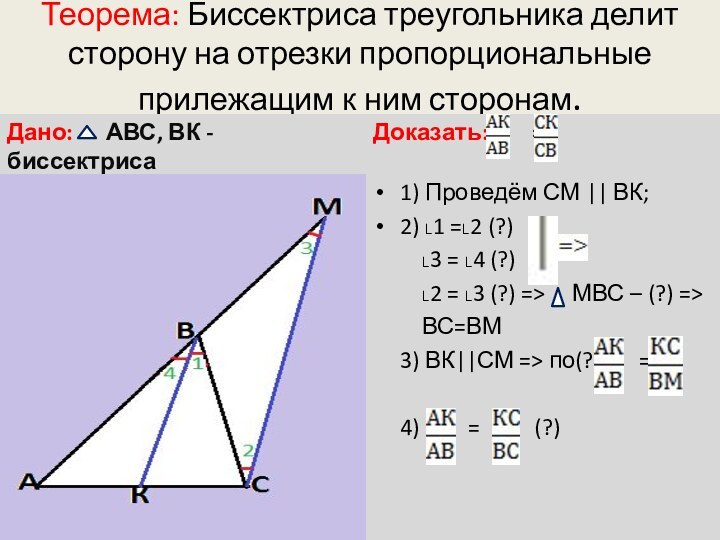
Слайд 26 Теорема: Биссектриса треугольника делит сторону на отрезки пропорциональные
прилежащим к ним сторонам.
Дано: АВС, ВК -
биссектрисаДоказать: =
1) Проведём СМ || ВК;
2) ˪1 =˪2 (?)
˪3 = ˪4 (?)
˪2 = ˪3 (?) => МВС – (?) =>
ВС=ВМ
3) ВК||СМ => по(?) =
4) = (?)





























