- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теорема Виета
Содержание
- 2. Проверка домашней работы №590
- 3. Ответьте на вопросыКак формулируется теорема Виета дляприведенного
- 4. Ответьте на вопросыКак Вы думаете, применима ли теорема Виета для неприведенного квадратного уравнения?
- 5. Решите уравнениеСвязаны ли корни уравнения с его коэффициентами?
- 6. Ответьте на вопросыМожем ли мы данное уравнение сделать приведенным?Как?Поделим уравнение на старший коэффициент.
- 7. Ответьте на вопросыПосле деления на старший коэффициент
- 8. Теорема Виета для неприведенного квадратного уравненияПусть квадратное
- 9. В геометрии мы сталкивались с тем, что
- 10. Давайте составим обратное утверждение для теоремы Виетауравнение
- 11. С помощью теоремы Виета проверим, правильно ли мы нашли корни.
- 12. Решение задач№580 (д,ж)Найдите сумму и произведение корней
- 13. Решение задач№580 (д,ж)Найдите сумму и произведение корней
- 14. Решение задач№581 (а)Решите уравнение и выполните проверку
- 15. №583 (а)Найдите подбором корни уравнения:Дискриминант D=81-4*20 –
- 16. Решите самостоятельно№594 (а)Не решая уравнение, выясните, имеет
- 17. Скачать презентацию
- 18. Похожие презентации
















Слайд 3
Ответьте на вопросы
Как формулируется теорема Виета для
приведенного квадратного
уравнения?
взятому с противоположным знаком, а произведение корней равно свободному члену
Слайд 4
Ответьте на вопросы
Как Вы думаете, применима ли теорема
Виета
для неприведенного квадратного уравнения?
Слайд 6
Ответьте на вопросы
Можем ли мы данное уравнение сделать
приведенным?
Как?
Поделим уравнение на старший коэффициент.
Слайд 7
Ответьте на вопросы
После деления на старший коэффициент корни
уравнения изменятся?
Как называются уравнения, имеющие одни и те же
корни?Подсказка: для ответа на вопрос обратитесь к учебнику (сведения за 7 класс, раздел «Уравнения», пункт 9)
Можем ли мы теперь применить теорему Виета?
Слайд 8
Теорема Виета для неприведенного квадратного уравнения
Пусть квадратное уравнение
имеет корни
Равносильное ему приведенное квадратное уравнение имеет вид:
Тогда
по теореме Виета:
Слайд 9 В геометрии мы сталкивались с тем, что для
некоторых утверждений будет верно и обратное утверждение.
Вспомните, как составляются
обратные утверждения.Если данное утверждение сформулировано в виде условного предложения ''если А, то В'', то обратным называется утверждение ''если В, то А'', то есть такое, у которого условием является заключение первого утверждения, а заключением - его же условие.
Слайд 10
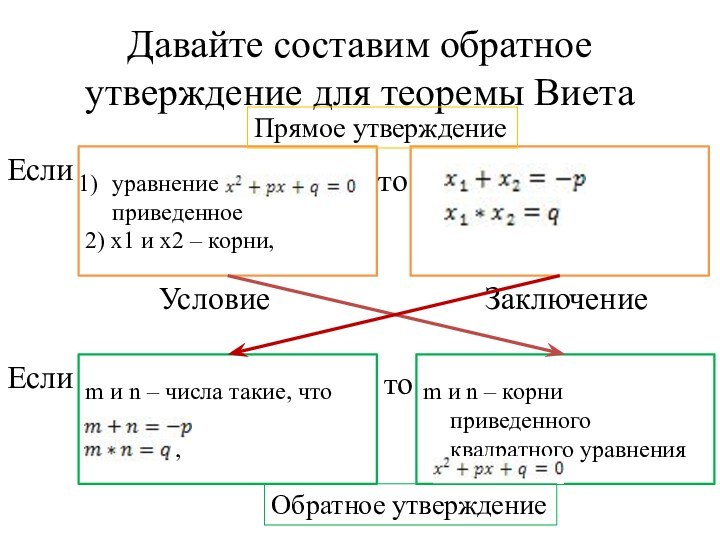
Давайте составим обратное утверждение для теоремы Виета
уравнение
приведенное
2)
x1 и x2 – корни,
Если
то
Условие
Заключение
m и n –
числа такие, что,
m и n – корни приведенного квадратного уравнения
Если
то
Обратное утверждение
Прямое утверждение
Слайд 12
Решение задач
№580 (д,ж)
Найдите сумму и произведение корней уравнения:
д)
По
теореме Виета для неприведенного квадратного уравнения:
Ответ: 4,5; -5
Слайд 13
Решение задач
№580 (д,ж)
Найдите сумму и произведение корней уравнения:
ж)
По
теореме Виета для неприведенного квадратного уравнения:
Ответ: -1; 0
Слайд 14
Решение задач
№581 (а)
Решите уравнение и выполните проверку по
теореме, обратной теореме Виета:
Найдем дискриминант:
По формуле корней квадратного уравнения
получаем:Покажем, что корни найдены правильно. В данном уравнении
коэффициент p равен -2, а свободный член q равен -9. Тогда:
Значит, по теореме, обратной теореме Виета, эти числа являются
корнями данного квадратного уравнения.
Ответ:
Слайд 15
№583 (а)
Найдите подбором корни уравнения:
Дискриминант D=81-4*20 – положительное
число. Пусть m и n –
корни уравнения. Тогда
Если
m и n – целые числа, то они являются делителями числа 20. Нужно учесть, что сумма этих чисел равна 9.
10*2
10+2=12
не подходит
-10*(-2)
-10-2=-12
не подходит
-5*(-4)
-5-4=-9
не подходит
5*4
5+4=9
подходит
Ответ: 5; 4