- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Цифровое моделирование.3
Содержание
- 2. Задачи, решаемые с помощью ЦМР.1Готовая цифровая модель
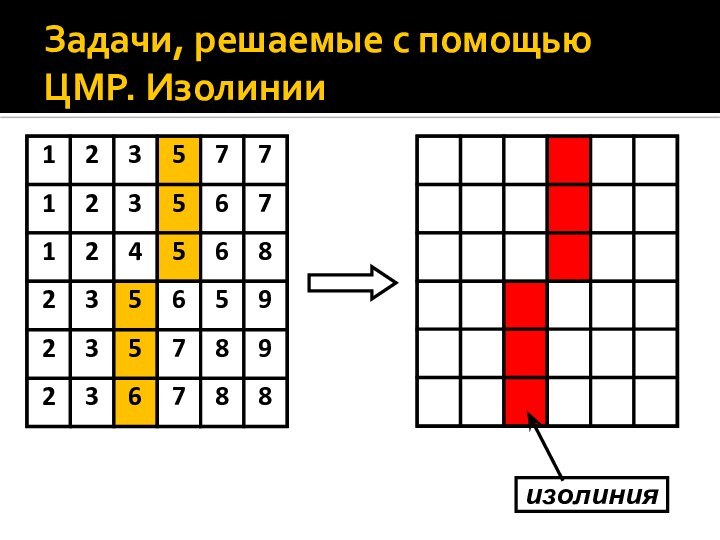
- 3. Задачи, решаемые с помощью ЦМР. Изолинии3
- 4. Задачи, решаемые с помощью ЦМР. Расчёт показателей рельефа
- 5. Задачи, решаемые с помощью ЦМР. Расчёт показателей
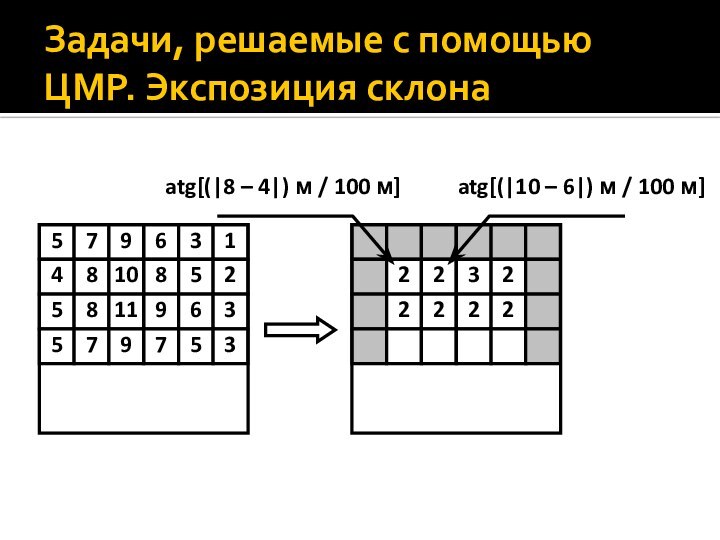
- 6. Задачи, решаемые с помощью ЦМР. Экспозиция склона
- 7. Задачи, решаемые с помощью ЦМР.5К другим задачам,
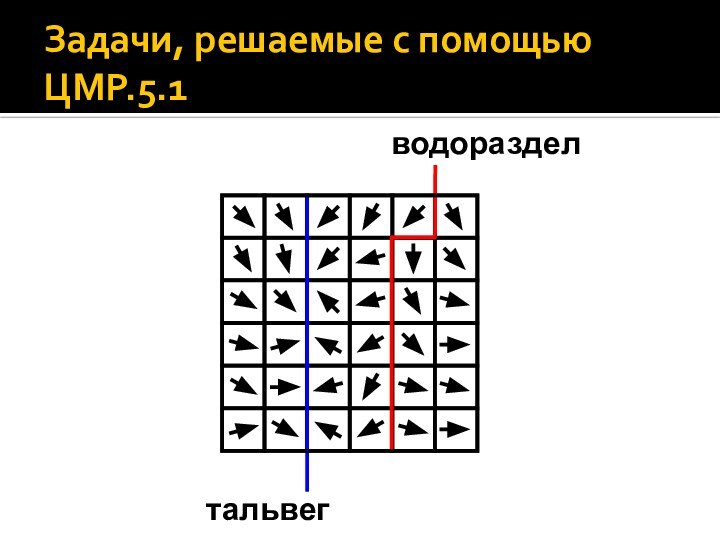
- 8. Задачи, решаемые с помощью ЦМР.5.1
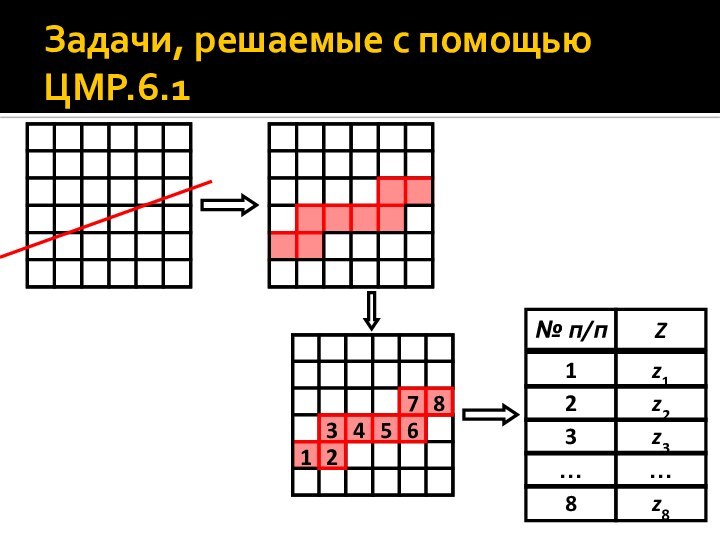
- 9. Задачи, решаемые с помощью ЦМР.6Следующий круг задач
- 10. Задачи, решаемые с помощью ЦМР.6.1
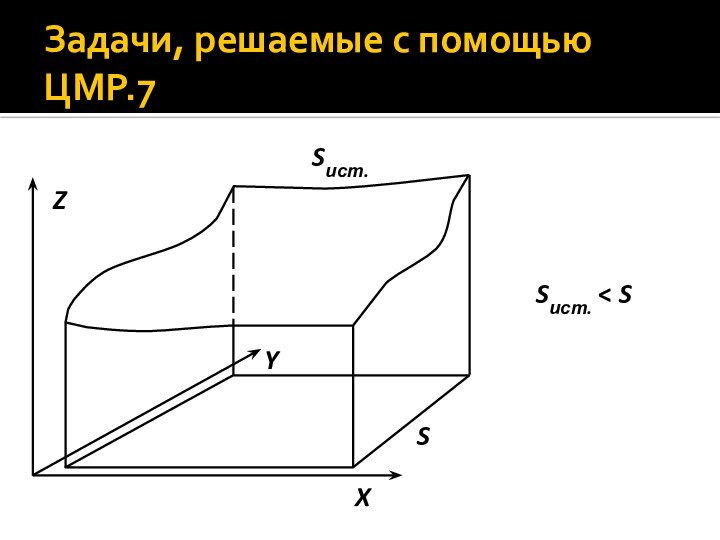
- 11. Задачи, решаемые с помощью ЦМР.7
- 12. Задачи, решаемые с помощью ЦМР.7.1В цифровых моделях
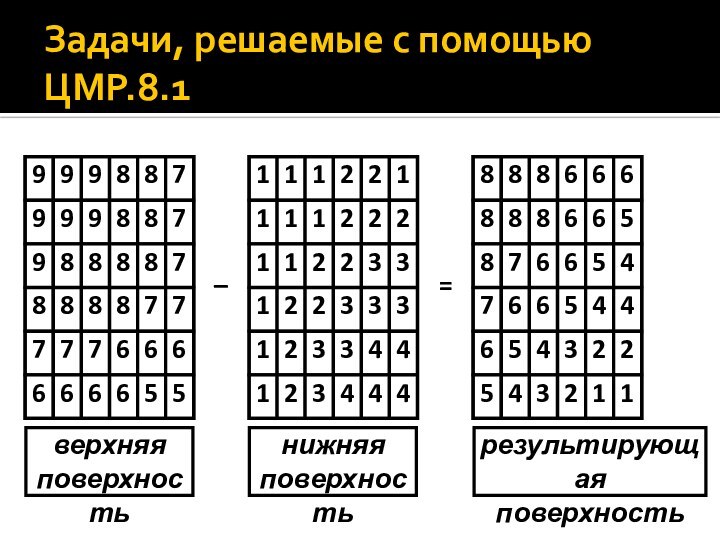
- 13. Задачи, решаемые с помощью ЦМР.8
- 14. Задачи, решаемые с помощью ЦМР.8.1
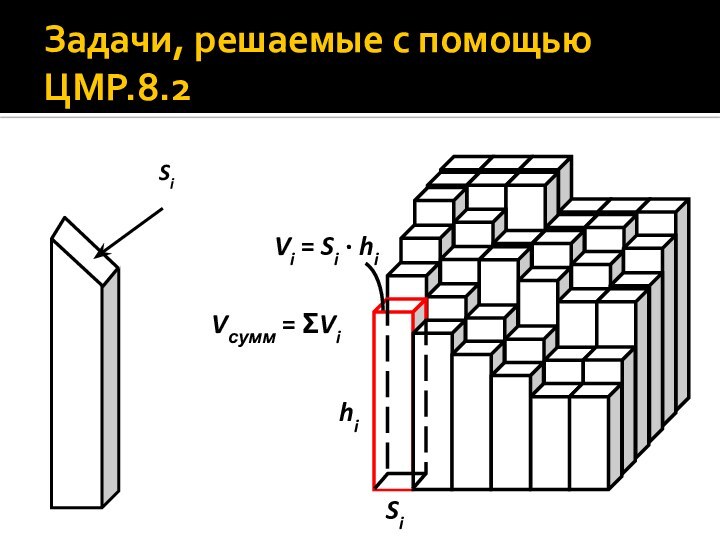
- 15. Задачи, решаемые с помощью ЦМР.8.2
- 16. Задачи, решаемые с помощью ЦМР.9Другая широко распространенная
- 17. Задачи, решаемые с помощью ЦМР.9.1
- 18. Задачи, решаемые с помощью ЦМР.9.2
- 19. Задачи, решаемые с помощью ЦМР.9.2
- 20. Задачи, решаемые с помощью ЦМР.9.2
- 21. Задачи, решаемые с помощью ЦМР.9.2
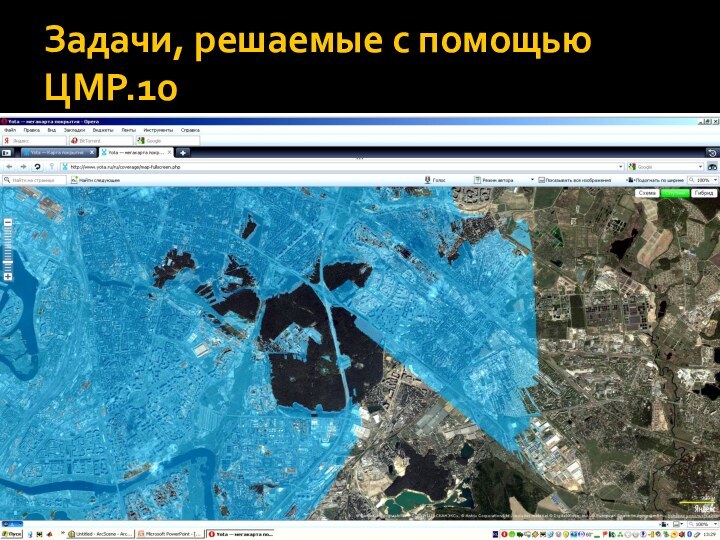
- 22. Задачи, решаемые с помощью ЦМР.10Наконец, к прикладным
- 23. Задачи, решаемые с помощью ЦМР.10
- 24. Автоматизация некоторых задача ГИС
- 25. ГенерализацияСуть картографической генерализации составляет отбор главного, существенного
- 26. Генерализация.2Стремление к автоматизации процессов картографической генерализации отмечалось уже на первых этапах применения компьютеров в картографии
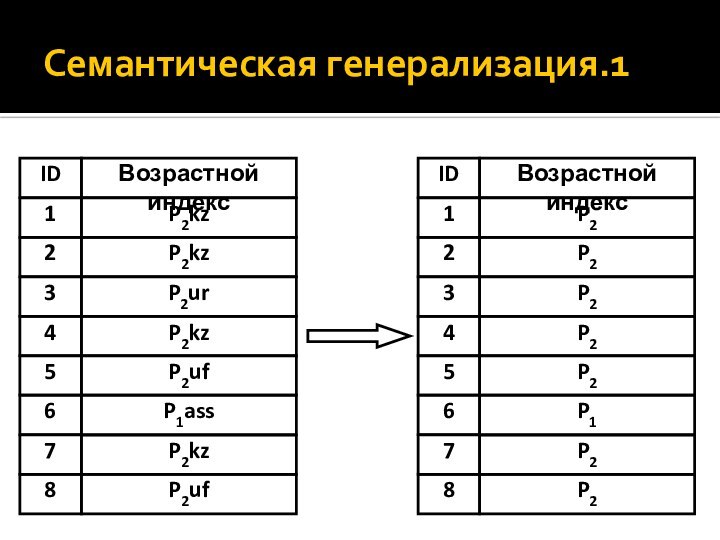
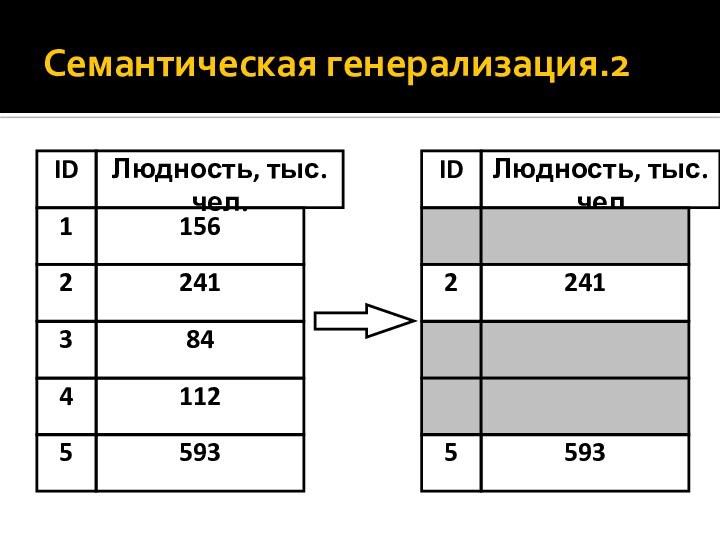
- 27. Виды генерализацииВ картографической генерализации выделяют две разновидности: семантическую (непространственную) геометрическую (пространственную).
- 28. Семантическая генерализация.1
- 29. Семантическая генерализация.2
- 30. Геометрическая генерализацияГеометрическая (пространственная) генерализация связана с правилами
- 31. Генерализация растрового формата Генерализация растрового формата может
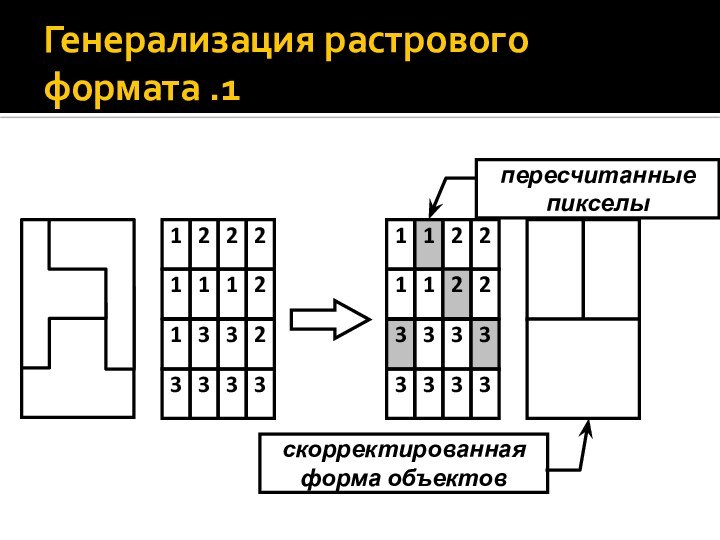
- 32. Генерализация растрового формата .1
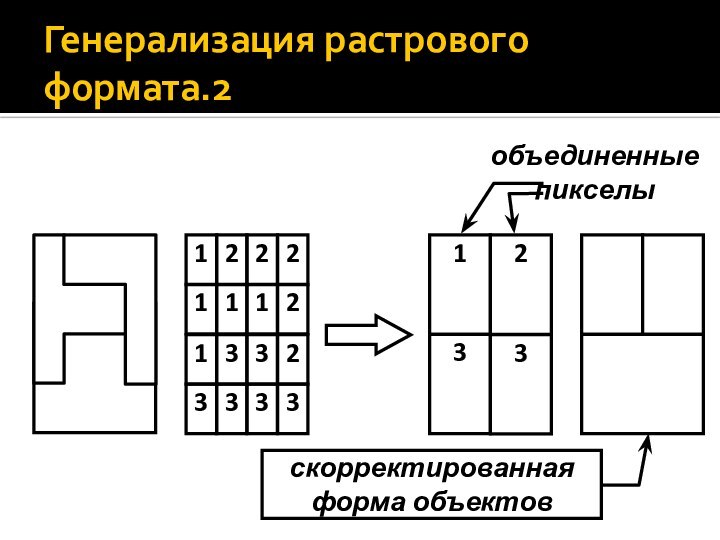
- 33. Генерализация растрового формата.2
- 34. Генерализация векторного формата упрощение сглаживаниекорректировка (или утрирование)перемещение слияние
- 35. УпрощениеВ лучшей степени разработаны приемы упрощения: они
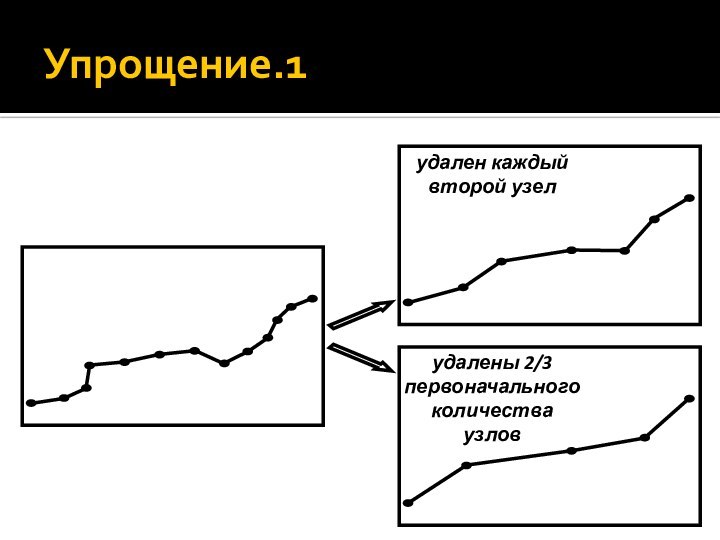
- 36. Упрощение.1
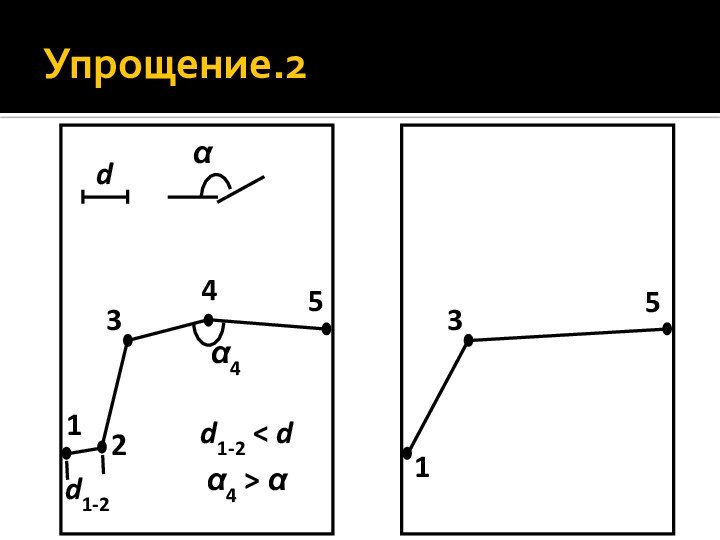
- 37. Упрощение.2
- 38. Упрощение.3
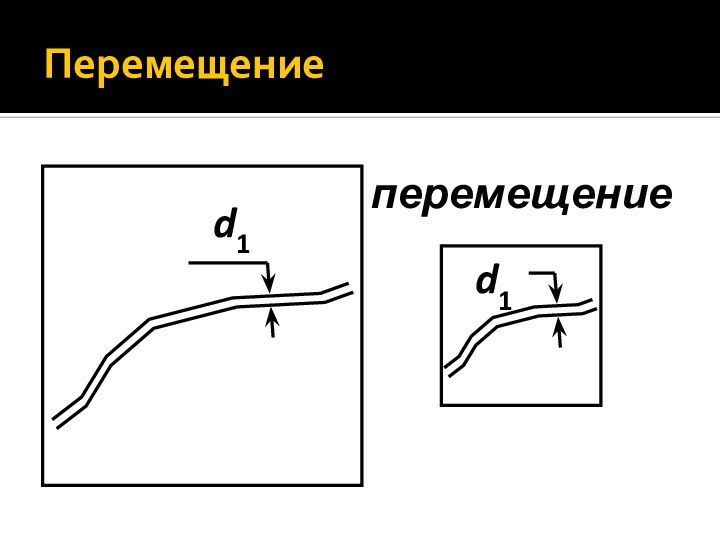
- 39. Перемещение
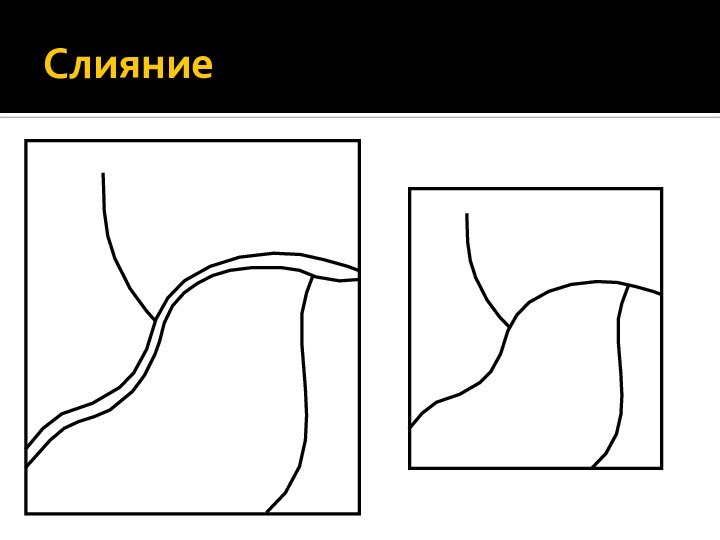
- 40. Слияние
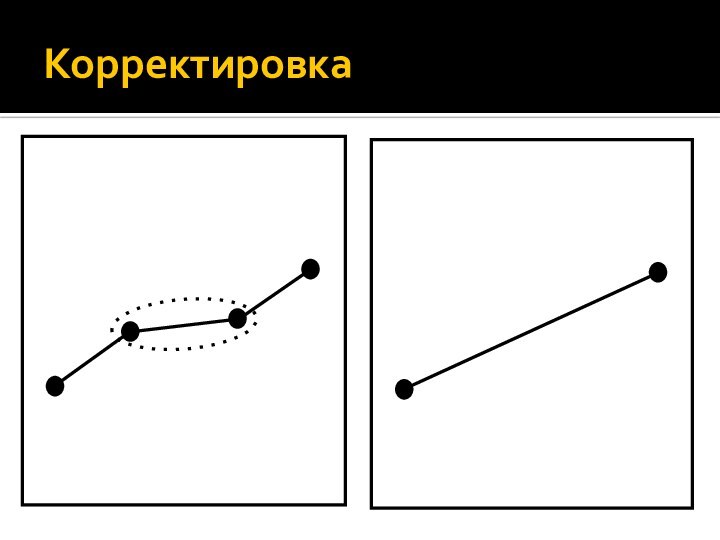
- 41. Корректировка
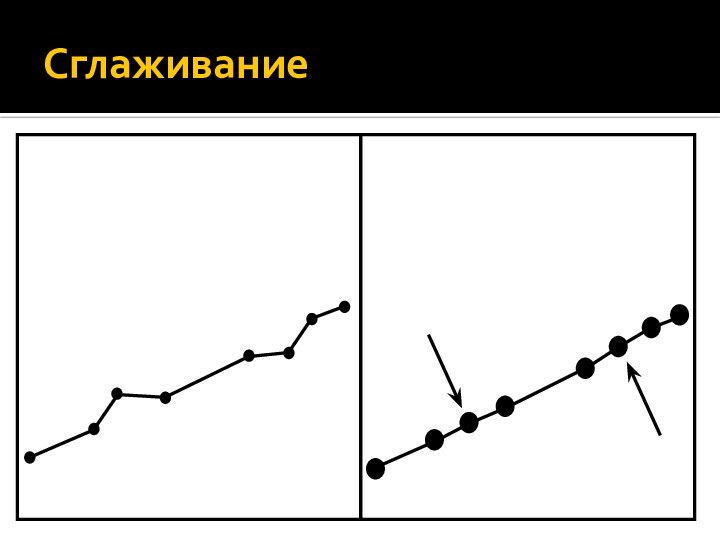
- 42. Сглаживание
- 43. Проверка качества генерализацииПоследним важным этапом генерализации является
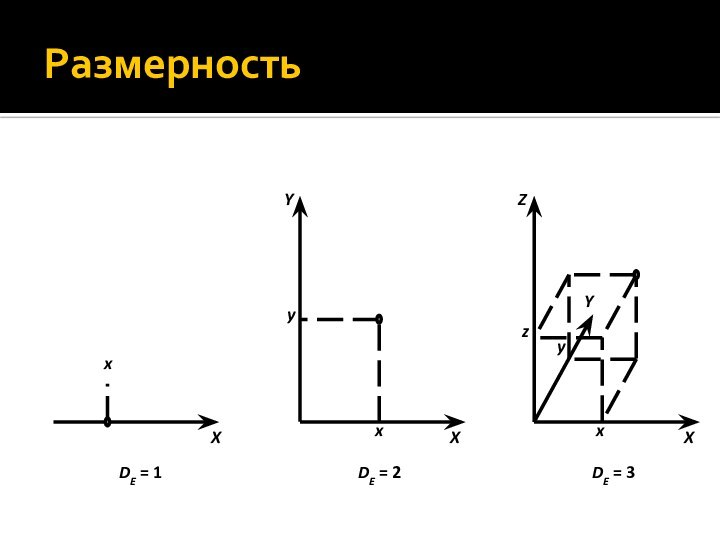
- 44. Размерность
- 45. Топологическая размерностьС евклидовой размерностью тесно связано понятие
- 46. Понятие фракталаТермин фрактал (от латинского слова fractus
- 47. Фрактальная размерностьВо фрактальной геометрии тоже действуют с
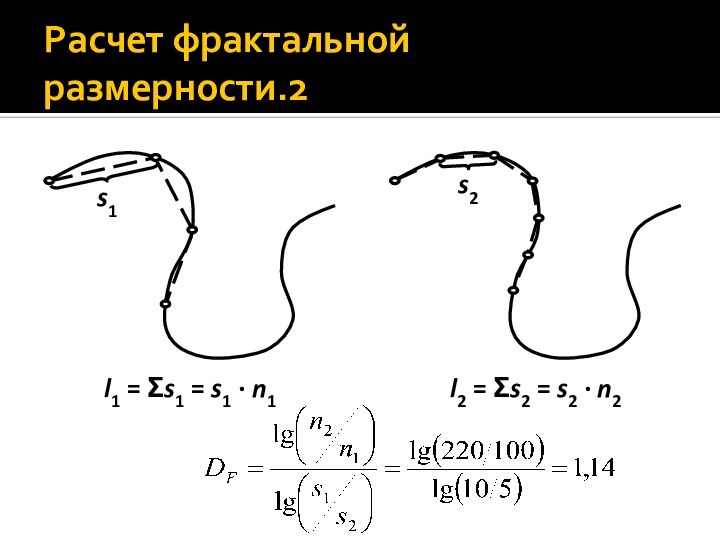
- 48. Расчет фрактальной размерностиИзмеряемую линию разбивают на отрезки
- 49. Расчет фрактальной размерности.2
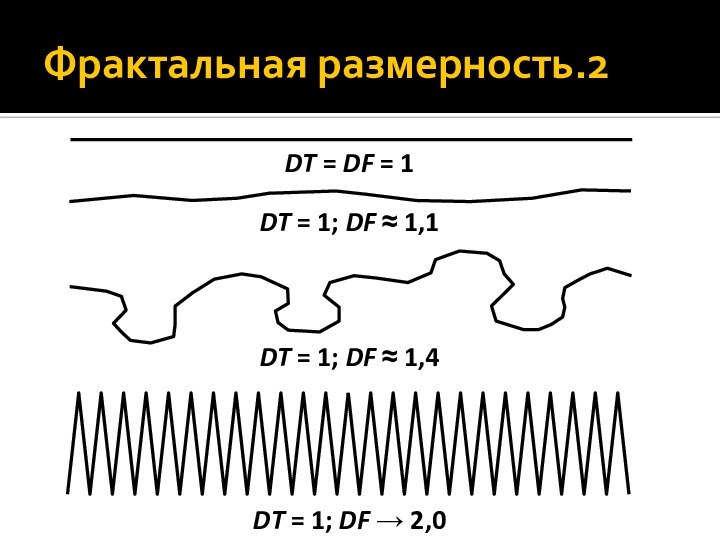
- 50. Фрактальная размерность.2
- 51. Фракталы и картографияС математическим определением фрактала связано
- 52. Скачать презентацию
- 53. Похожие презентации
Задачи, решаемые с помощью ЦМР.1Готовая цифровая модель рельефа способна обеспечить решение самых разнообразных задач. Первая группа задач связана с нахождением по ЦМР высот произвольных точек. Обычно на растровую модель наносится искомая точка, высота пиксела, в который
Слайд 5
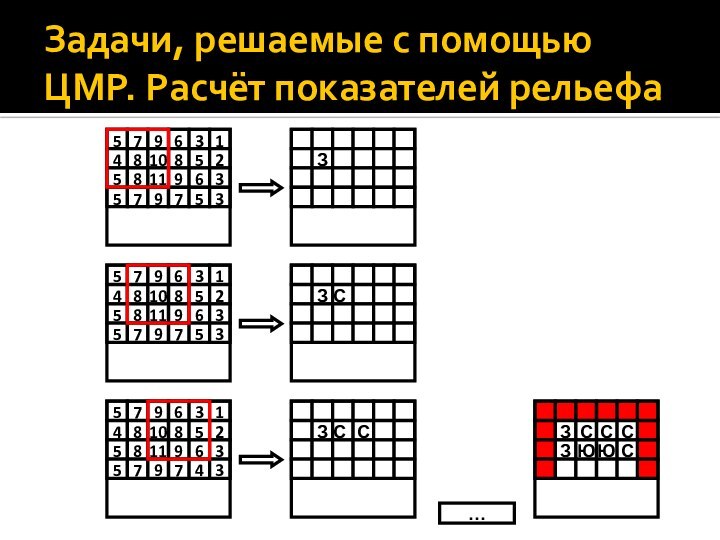
Задачи, решаемые с помощью ЦМР. Расчёт показателей рельефа
Крутизна
склона α есть арктангенс превышения высот двух точек Δh
к горизонтальному проложению l между ними: .Применительно к GRID-модели это означает, что последовательно в 9 соседних точках находится |Δhmax| – максимальная разница без учета знака в высотах между центральным пикселем и прочими, которая делится на геометрический размер пиксела в масштабе карты, после чего извлекается арктангенс.
Слайд 7
Задачи, решаемые с помощью ЦМР.5
К другим задачам, решаемым
по ЦМР, можно отнести расчет сепаратрисс – структурных линий
рельефа, а именно тальвегов и водоразделов.
Слайд 9
Задачи, решаемые с помощью ЦМР.6
Следующий круг задач связан
с построением профилей высот (орографические профили) по направлению прямой
или ломаной линии.
Слайд 12
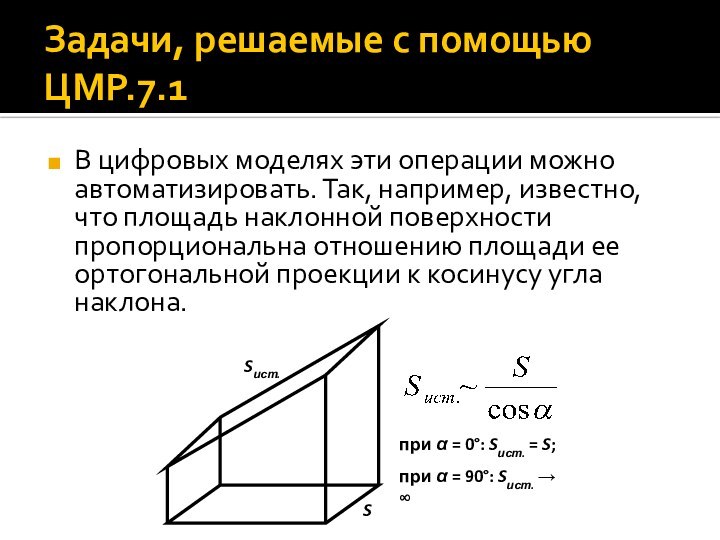
Задачи, решаемые с помощью ЦМР.7.1
В цифровых моделях эти
операции можно автоматизировать. Так, например, известно, что площадь наклонной
поверхности пропорциональна отношению площади ее ортогональной проекции к косинусу угла наклона.
Слайд 16
Задачи, решаемые с помощью ЦМР.9
Другая широко распространенная функция
работы с ЦМР – трехмерная визуализация в виде блок-диаграмм,
светотеневой отмывки и т.п.
Слайд 22
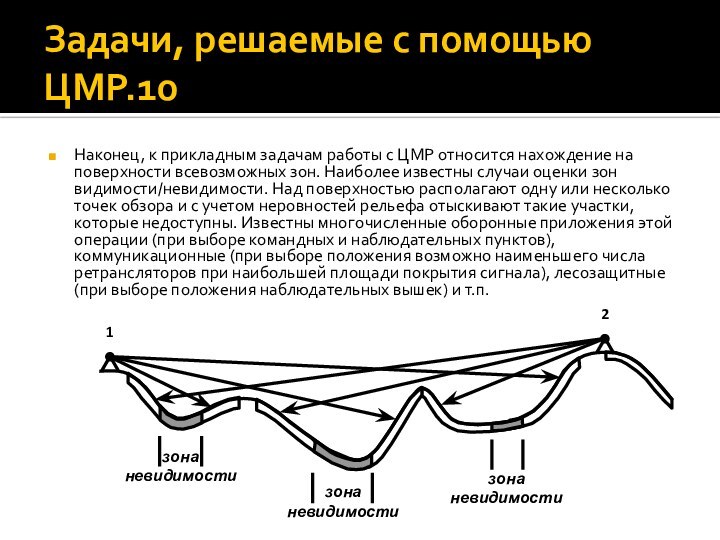
Задачи, решаемые с помощью ЦМР.10
Наконец, к прикладным задачам
работы с ЦМР относится нахождение на поверхности всевозможных зон.
Наиболее известны случаи оценки зон видимости/невидимости. Над поверхностью располагают одну или несколько точек обзора и с учетом неровностей рельефа отыскивают такие участки, которые недоступны. Известны многочисленные оборонные приложения этой операции (при выборе командных и наблюдательных пунктов), коммуникационные (при выборе положения возможно наименьшего числа ретрансляторов при наибольшей площади покрытия сигнала), лесозащитные (при выборе положения наблюдательных вышек) и т.п.
Слайд 25
Генерализация
Суть картографической генерализации составляет отбор главного, существенного и
его целенаправленное обобщение. Задачи генерализации приходится решать всегда при
создании мелкомасштабных карт по крупномасштабным источникам.
Слайд 26
Генерализация.2
Стремление к автоматизации процессов картографической генерализации отмечалось уже
на первых этапах применения компьютеров в картографии
Слайд 27
Виды генерализации
В картографической генерализации выделяют две разновидности:
семантическую
(непространственную)
геометрическую (пространственную).
Слайд 30
Геометрическая генерализация
Геометрическая (пространственная) генерализация связана с правилами отображения
формы, размера и положения географических объектов в плоскости карты.
Она проявляется в обобщении геометрических очертаний объектов, спрямлении границ, отказе от мелких деталей, группировке контуров. Формальные (механические) подходы к пространственной генерализации не годятся. В настоящее время проблема автоматизированной генерализации пространственных данных далека от завершения, поскольку пока еще слабо разработаны принципы распознавания образов и иерархической структуры геометрических данных.Методы автоматизированного отбора и обобщения различаются для растрового и векторного формата представления данных.
Слайд 31
Генерализация растрового формата
Генерализация растрового формата может быть
реализована в разных вариантах, но так или иначе всегда
опирается на существующую сетку пикселов
Слайд 34
Генерализация векторного формата
упрощение
сглаживание
корректировка (или утрирование)
перемещение
слияние
Слайд 35
Упрощение
В лучшей степени разработаны приемы упрощения: они лучше
формализуются и к ним чаще приходится прибегать при автоматизированной
генерализации. В зависимости от критериев выбора точек на удаление все они делятся на три группы алгоритмов.Алгоритмы независимых точек
Алгоритмы локальной обработки.
Алгоритмаы глобальной обработки
Слайд 43
Проверка качества генерализации
Последним важным этапом генерализации является оценка
ее качества. Единственным объективным критерием такой оценки служит субъективное
мнение картографа. Только его компетенция, опыт и профессиональная интуиция могут служить мерой корректности картографической (в т.ч. автоматизированной) генерализации. Каких-либо формальных критериев, отвечавших бы на вопрос «хорошо или плохо проведена генерализация?», – нет. С этих позиций последний этап генерализации даже сложнее, чем собственно генерализация.В автоматизированной генерализации попытки формализованной оценки полученных результатов известны давно, но наиболее продуктивным оказывается применение теории фракталов.
Слайд 45
Топологическая размерность
С евклидовой размерностью тесно связано понятие топологической
размерности объектов DT, под которой понимают «мерность» объектов. В
обычной евклидовой геометрии, которую в основном используют для представления географической реальности, оперируют с точками, линиями, площадями и объемами. Точки имеют топологическую размерность DT равную 0, линии – 1, площади – 2, объемы – 3. Топологическая размерность DT не может быть выше евклидовой DE. Это значит, что на плоскости с эвклидовой размерностью DE 2 можно изобразить точку (DT = 0), линию (DT = 1) и площадной полигон (DT = 2), но нельзя изобразить объемное тело (DT = 3).
Слайд 46
Понятие фрактала
Термин фрактал (от латинского слова fractus –
дробный), был предложен Бенуа Мандельбротом в 1975 году для
обозначения нерегулярных самоподобных математических структур.
Слайд 47
Фрактальная размерность
Во фрактальной геометрии тоже действуют с точками,
линиями, площадями и объемами, но не ограничиваются целочисленной размерностью,
а вводят понятие фрактальной размерности DF, которая может выражаться любым действительным числом в интервале от топологической до евклидовой размерности, включая границы: ∞ > DE ≥ DF ≥ DT ≥ 0.
Слайд 48
Расчет фрактальной размерности
Измеряемую линию разбивают на отрезки заданной
длины s1 и подсчитывают число таких отрезков n1. Тогда
длина линии l1 равна s1 · n1. Если длина шага s1 равна 10 м, а число шагов n1 – 100, длина линии составит 1 000 м. Затем процесс повторяют, уменьшив длину отрезков до s2, соответственно увеличится их число – n2. Длина линии l2 в этом случае будет равна произведению s2 на n2, причем l2 ≥ l1. Допустим, s2 равно 5 м, а n2 – 220, длина l2 составит 1 100 м.
Слайд 51
Фракталы и картография
С математическим определением фрактала связано важное
