Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Условная вероятность - практика

Содержание

2. Условная вероятностьВероятность события A при условии того, что событие B произошло, называется условной вероятностью и обозначается или
3. Пример 1.Пусть пять студентов вытягивают на экзамене
4. Решение задачиПусть пять студентов вытягивают на экзамене
5. Формула полной вероятностиДля вычисления полной вероятности события
6. Формула БайесаПусть событие A может быть вызвано
7. Пример 2.Имеются 2 урны с шарами. В
8. Пример 2.1Имеются 2 урны с шарами. В
9. Пример 2.2Имеются 2 урны с шарами. В
10. Пример 2.3Имеются 2 урны с шарами. В
12. Скачать презентацию
13. Похожие презентации

Условная вероятностьВероятность события A при условии того, что событие B произошло, называется условной вероятностью и обозначается или

Главная
Разное
Условная вероятность - практика

Условная вероятностьВероятность события A при условии того, что событие B произошло, называется условной вероятностью и обозначается или

Пример 1.Пусть пять студентов вытягивают на экзамене один билет из пяти, причем

Решение задачиПусть пять студентов вытягивают на экзамене один билет из пяти, причем

Формула полной вероятностиДля вычисления полной вероятности события A нужно перечислить все условия

Формула БайесаПусть событие A может быть вызвано набором причин Hi. Тогда вероятность

Пример 2.Имеются 2 урны с шарами. В первой урне находятся 2 белых

Пример 2.1Имеются 2 урны с шарами. В первой урне находятся 2 белых

Пример 2.2Имеются 2 урны с шарами. В первой урне находятся 2 белых

Пример 2.3Имеются 2 урны с шарами. В первой урне находятся 2 белых

Дерево исходовCBACAACBBCACABACBACBABCВаш выборB1/31/31/31/31/31/31/31/21/31/31/31/31/311/2111/21/21/21/2111Не меняет выбор и выигрываетМеняет выбор и выигрывает

Слайды презентации

Слайд 2 Условная вероятность
Вероятность события A при условии того, что событие B произошло, называется условной вероятностью

и обозначается
или

Слайд 3 Пример 1.
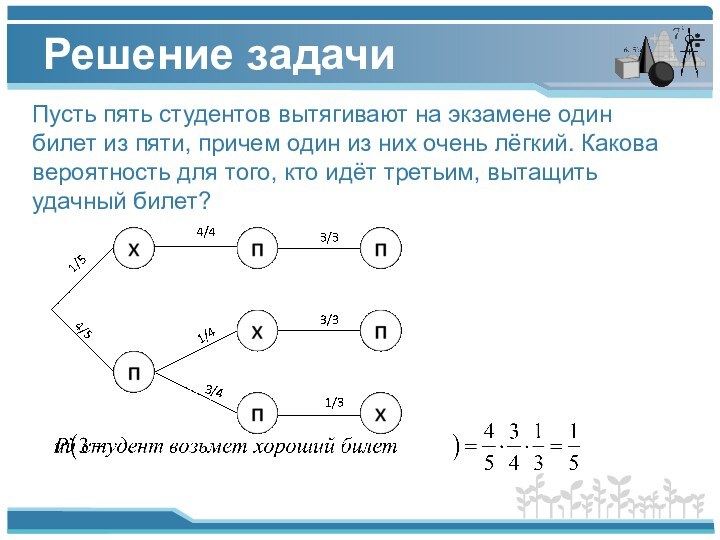
Пусть пять студентов вытягивают на экзамене один

Пример 1.Пусть пять студентов вытягивают на экзамене один билет из пяти,

билет из пяти, причем один из них - очень

лёгкий. Какова вероятность для того, кто идёт третьим, вытащить удачный билет?
Решение.

Очевидно, что эта вероятность зависит от того, что попалось предыдущим студентам, и вытянуть удачный билет третий студент может только в том случае, когда его не взяли двое предыдущих:

Слайд 4 Решение задачи
Пусть пять студентов вытягивают на экзамене один

Решение задачиПусть пять студентов вытягивают на экзамене один билет из пяти,

билет из пяти, причем один из них очень лёгкий.

Какова вероятность для того, кто идёт третьим, вытащить удачный билет?

Слайд 5 Формула полной вероятности
Для вычисления полной вероятности события A

Формула полной вероятностиДля вычисления полной вероятности события A нужно перечислить все

нужно перечислить все условия Hi, при которых может наступить

A, и перемножить вероятности этих условий на соответствующие им условные вероятности.

Причем сумма вероятностей гипотез должна быть равна 1, т.е.

Слайд 6 Формула Байеса
Пусть событие A может быть вызвано набором

Формула БайесаПусть событие A может быть вызвано набором причин Hi. Тогда

причин Hi. Тогда вероятность того, что к событию A

привело событие Hi, пропорциональна произведению вероятности соответствующей причины на вероятность следствия.

Слайд 7 Пример 2.
Имеются 2 урны с шарами. В первой

Пример 2.Имеются 2 урны с шарами. В первой урне находятся 2

урне находятся 2 белых и 4 черных шара, во

второй – 3 белых и 3 черных.
Из каждой урны достали по одному шару. Найти вероятность того, что эти шары белые.
Выбирается урна и из нее извлекается 2 шара. Найти вероятность того, что эти шары белые. Найти вероятность того, что они были взяты из первой урны.
Из первой урны во вторую переложили 1 шар, а затем из второй (пополненной) урны достали 2 шара. Они оказались белыми. Найти вероятность того, что был переложен белый шар.

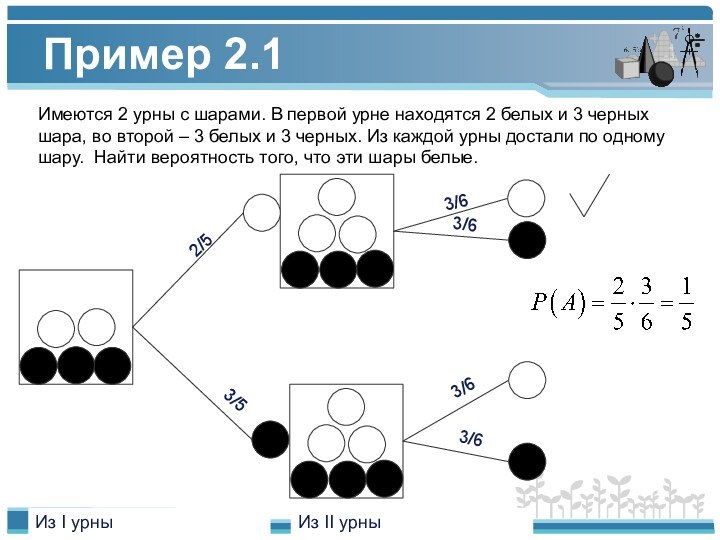
Слайд 8 Пример 2.1
Имеются 2 урны с шарами. В первой

Пример 2.1Имеются 2 урны с шарами. В первой урне находятся 2

урне находятся 2 белых и 3 черных шара, во

второй – 3 белых и 3 черных. Из каждой урны достали по одному шару. Найти вероятность того, что эти шары белые.

3/5

3/6

2/5

3/6

Из I урны

Из II урны

Слайд 9 Пример 2.2
Имеются 2 урны с шарами. В первой

Пример 2.2Имеются 2 урны с шарами. В первой урне находятся 2

урне находятся 2 белых и 3 черных шара, во

второй – 3 белых и 3 черных. Выбирается урна и из нее извлекается 2 шара. Найти вероятность того, что эти шары белые. Найти вероятность того, что они были взяты из первой урны.

1/2

3/6

3/5

1/4

2/5

2/4

2/5

3/5

2/5

3/4

Слайд 10 Пример 2.3
Имеются 2 урны с шарами. В первой

Пример 2.3Имеются 2 урны с шарами. В первой урне находятся 2

урне находятся 2 белых и 4 черных шара, во

второй – 3 белых и 3 черных. Из первой урны во вторую переложили 1 шар, а затем из второй (пополненной) урны достали 2 шара. Они оказались белыми. Найти вероятность того, что был переложен белый шар.