Слайд 2
Введение
Статистическое исследование может осуществляться по данным несплошного наблюдения,
основная цель которого состоит в получении характеристик изучаемой совокупности
по обследованной ее части. Одним из наиболее распространенных в статистике методов, применяющих несплошное наблюдение, является выборочный метод.
Под выборочным понимается метод статистического исследования, при котором обобщающие показатели изучаемой совокупности устанавливаются по некоторой ее части на основе положений случайного отбора. При выборочном методе обследованию подвергается сравнительно небольшая часть всей изучаемой совокупности (обычно до 5 - 10%, реже до 15 - 25%).
Слайд 3
Введение
Значение выборочного метода состоит в том, что при
минимальной численности обследуемых единиц проведение исследования осуществляется в более
короткие сроки и с минимальными затратами труда и средств. Это повышает оперативность статистической информации, уменьшает ошибки регистрации.
В проведении ряда исследований выборочный метод является единственно возможным, например, при контроле качества продукции (товара), если проверка сопровождается уничтожением или разложением на составные части обследуемых образцов (определение сахаристости фруктов, клейковины печеного хлеба, установление носкости обуви, прочности тканей на разрыв и т.д.).
Слайд 4
Введение
Проведение исследования социально — экономических явлений выборочным методом
складывается из ряда последовательных этапов:
1) обоснование (в соответствии с
задачами исследования) целесообразности применения выборочного метода;
2) составление программы проведения статистического исследования выборочным методом;
3) решение организационных вопросов сбора и обработки исходной информации;
4) установление доли выборки, т.е. части подлежащих обследованию единиц генеральной совокупности;
5) обоснование способов формирования выборочной совокупности;
6) осуществление отбора единиц из генеральной совокупности для их обследования;
7) фиксация в отобранных единицах (пробах) изучаемых признаков;
8) статистическая обработка полученной в выборке информации с определением обобщающих характеристик изучаемых признаков;
9) определение количественной оценки ошибки выборки;
10) распространение обобщающих выборочных характеристик на генеральную совокупность.
Слайд 5
Введение
В генеральной совокупности доля единиц, обладающих изучаемым признаком,
называется генеральной долей (обозначается р), а средняя величина изучаемого
варьирующего признака — генеральной средней (обозначается ).
В выборочной совокупности долю изучаемого признака называют выборочной долей, или частостью (обозначается ), а среднюю величину в выборке — выборочной средней (обозначается ).
Слайд 6
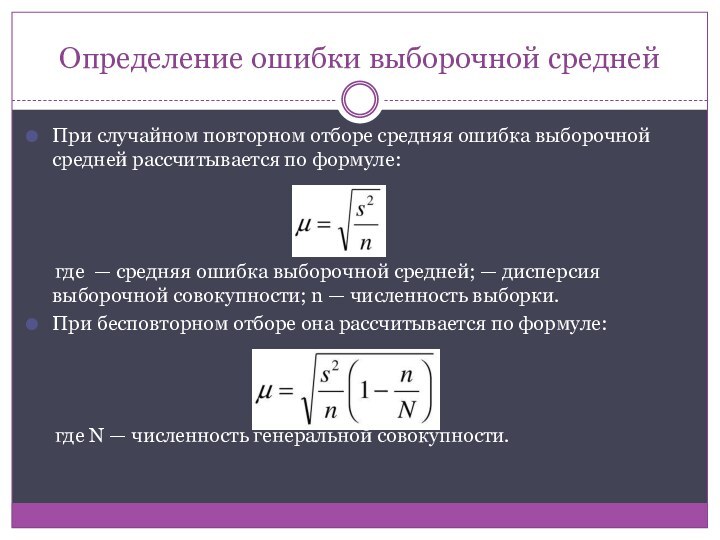
Определение ошибки выборочной средней
При случайном повторном отборе средняя
ошибка выборочной средней рассчитывается по формуле:
где
— средняя ошибка выборочной средней; — дисперсия выборочной совокупности; n — численность выборки.
При бесповторном отборе она рассчитывается по формуле:
где N — численность генеральной совокупности.
Слайд 7
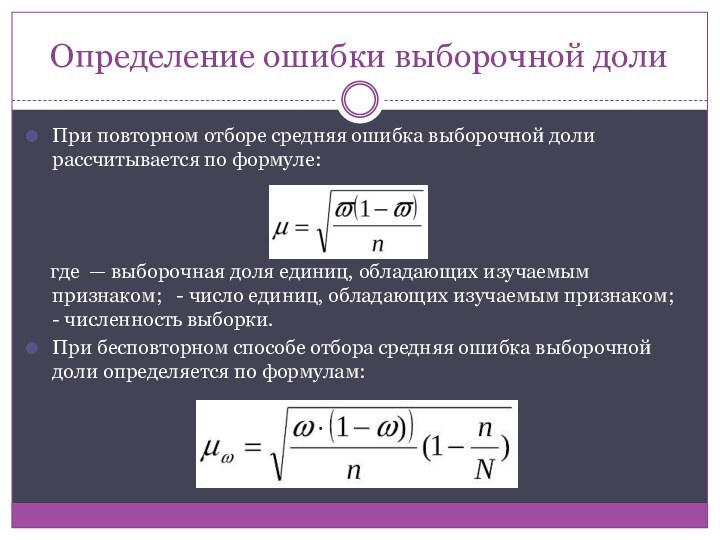
Определение ошибки выборочной доли
При повторном отборе средняя ошибка
выборочной доли рассчитывается по формуле:
где — выборочная
доля единиц, обладающих изучаемым признаком; - число единиц, обладающих изучаемым признаком; - численность выборки.
При бесповторном способе отбора средняя ошибка выборочной доли определяется по формулам:
Слайд 8
Определение ошибки выборочной доли
Предельная ошибка выборки связана со
средней ошибкой выборки отношением:
При этом t как коэффициент
кратности средней ошибки выборки зависит от значения вероятности Р, с которой гарантируется величина предельной ошибки выборки.
Предельная ошибка выборки при бесповторном отборе определяется по следующим формулам:
Слайд 9
Определение ошибки выборочной доли
Предельная ошибка выборки при повторном
отборе определяется по формуле:
Слайд 10
Малая выборка
При контроле качества товаров в экономических исследованиях
эксперимент может проводиться на основе малой выборки. Под малой
выборкой понимается несплошное статистическое обследование, при котором выборочная совокупность образуется из сравнительно небольшого числа единиц генеральной совокупности. Объем малой выборки обычно не превышает 30 единиц и может доходить до 4 — 5 единиц.
Слайд 11
Малая выборка
Средняя ошибка малой выборки вычисляется по формуле:
где — дисперсия малой
выборки.
При определении дисперсии число степеней свободы равно n-1:
Предельная ошибка малой выборки определяется по формуле :
Слайд 12
Способы распространения характеристик выборки на генеральную совокупность
Выборочный метод
чаще всего применяется для получения характеристик генеральной совокупности по
соответствующим показателям выборки. В зависимости от целей исследований это осуществляется или прямым пересчётом показателей выборки для генеральной совокупности, или посредством расчёта поправочных коэффициентов.
Способ прямого пересчёта. Он состоит в том, что показатели выборочной доли или средней распространяется на генеральную совокупность с учётом ошибки выборки.
Так, в торговле определяется количество поступивших в партии товара нестандартных изделий. Для этого (с учётом принятой степени вероятности) показатели доли нестандартных изделий в выборке умножаются на численность изделий во всей партии товара.
Слайд 13
Способы отбора единиц из генеральной совокупности
Основным условием проведения
выборочного обследования является предупреждение возникновения систематических ошибок, возникающих вследствие
нарушения принципа равных возможностей попадания в выборку каждой единицы генеральной совокупности. Предупреждение систематических ошибок достигается в результате применения научно обоснованных способов формирования выборочной совокупности.
Слайд 14
Способы отбора единиц из генеральной совокупности
Существуют следующие способы
отбора единиц из генеральной совокупности:
1) индивидуальный отбор — в
выборку отбираются отдельные единицы;
2) групповой отбор — в выборку попадают качественно однородные группы или серии изучаемых единиц;
3) комбинированный отбор — это комбинация индивидуального и группового отбора.
Способы отбора определяются правилами формирования выборочной совокупности.
Выборка может быть:
собственно-случайная;
механическая;
типическая;
серийная;
комбинированная.
Слайд 15
Способы отбора единиц из генеральной совокупности
1) Собственно-случайная выборка
состоит в том, что выборочная совокупность образуется в результате
случайного (непреднамеренного) отбора отдельных единиц из генеральной совокупности. При этом количество отобранных в выборочную совокупность единиц обычно определяется исходя из принятой доли выборки. Доля выборки есть отношение числа единиц выборочной совокупности n к численности единиц генеральной совокупности N, т.е.
Слайд 16
Способы отбора единиц из генеральной совокупности
2) Механическая выборка
состоит в том, что отбор единиц в выборочную совокупность
производится из генеральной совокупности, разбитой на равные интервалы (группы). При этом размер интервала в генеральной совокупности равен обратной величине доли выборки.
Важной особенностью механической выборки является то, что формирование выборочной совокупности можно осуществить, не прибегая к составлению списков. На практике часто используют тот порядок, в котором фактически размещаются единицы генеральной совокупности. Например, последовательность выхода готовых изделий с конвейера или поточной линии, порядок размещения единиц партии товара при хранении, транспортировке, реализации и т.д.
Слайд 17
Способы отбора единиц из генеральной совокупности
3) Типическая выборка.
При типической выборке генеральная совокупность вначале расчленяется на однородные
типические группы. Затем из каждой типической группы собственно-случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность.
Типическая выборка обычно применяется при изучении сложных статистических совокупностей. Например, при выборочном обследовании производительности труда работников торговли, состоящих из отдельных групп по квалификации. Важной особенностью типической выборки является то, что она дает более точные результаты по сравнению с другими способами отбора единиц в выборочную совокупность.
Слайд 18
Способы отбора единиц из генеральной совокупности
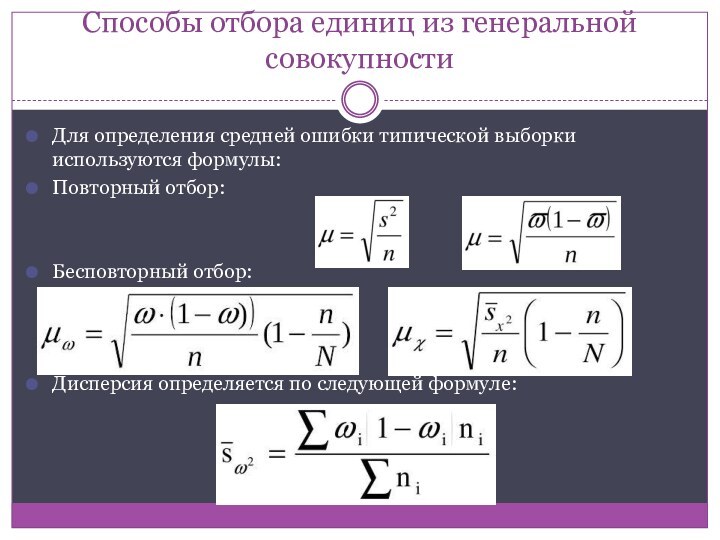
Для определения средней
ошибки типической выборки используются формулы:
Повторный отбор:
Бесповторный отбор:
Дисперсия определяется
по следующей формуле: