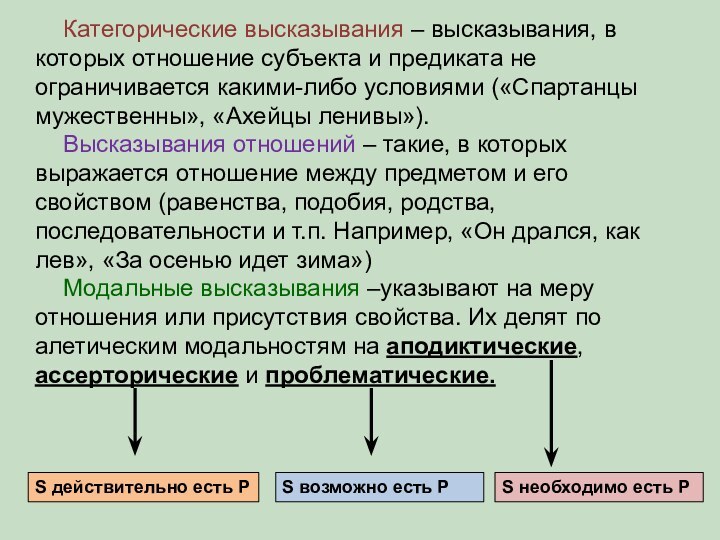
логическая операция, при которой термины высказывания меняются местами (субъект
становится предикатом, и наоборот)
Все полные люди добродушны
Некоторые добряки – полные
Превращение (обверсия) – логическая операция, при которой меняется качество высказывания (утвердительное становится отрицательным, и наоборот)
Ни один моряк не является рыбаком
Все моряки являются нерыбаками
Противопоставление (контрапозиция) – операция, при которой производится обращение, а затем превращение, или наоборот (противопоставление субъекту и противопоставление предикату)
Все японцы занимаются сумо
Некоторые сумоисты – японцы
Некоторые сумоисты не являются не японцами
Ни один буддист не является даосом
Все буддисты – не даосы
Некоторые не даосы – буддисты