Презентация на тему Закон тождества

значит не иметь ни одного значения; если же у

слов нет значений, тогда утрачена всякая возможность рассуждать друг с другом, а в действительности — и с самим собой; ибо невозможно ничего мыслить, если не мыслить что-нибудь одно. (Аристотель)
Всякое утверждение в правильном мышлении  имеет однозначный смысл и не подменяется другим утверждением.
Если высказывание истинно, то оно истинно.

мысль

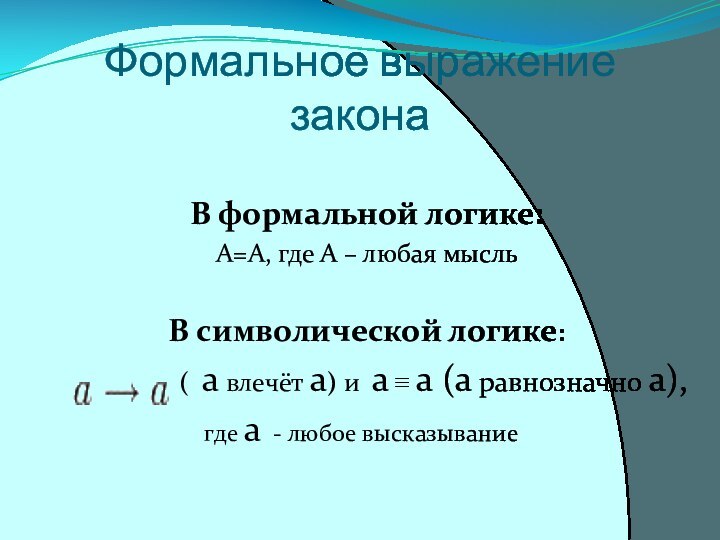
В символической логике:  

( a влечёт а) и а ≡ а (а равнозначно а),
где а - любое высказывание

влечет за собой возникновение логических ошибок, которые называются  паралогизмами.

Преднамеренное нарушение совершается для того, чтобы запутать собеседника и доказать ему какую-нибудь ложную мысль, тогда появляются не просто ошибки, а софизмы.

или непреднамеренная логическая ошибка в мышлении (в доказательстве, в споре, диалоге),

возникающая при нарушении законов или правил логики и приводящая к ошибочному выводу
Софизм - ложное высказывание, которое, тем не менее, при поверхностном рассмотрении кажется правильным. Софизм основан на преднамеренном, сознательном нарушении правил логики. Это отличает его от паралогизма.

речи
Неумение вникать в смысл утверждений

логическая ошибка, в основе которой лежит двусмысленность языковых выражений.

 
Эквивокация или подмена понятий (от лат. равноголосие, двусмысленность) - логическая ошибка при рассуждении, в основе которой лежит использование одного и того же слова в разных значениях.
Логомахия (от греч. бой, сражение) спор о словах, когда в процессе дискуссии участники не могут прийти к единой точке зрения в силу того, что не уточнили исходные понятия.

данного закона используется для создания комического эффекта, например в

литературных произведениях, анекдотах, задачах и головоломках. В основе всех фокусов также лежит нарушение закона тождества.

~ B)

Пример: «Неверно, что будет холодно и будет дождливо, тогда

и только тогда, когда завтра не будет холодно или завтра не будет дождливо»

А & ~ В)

Пример: «Неверно, что человек читает газеты или читает

журналы, тогда и только тогда, когда он не читает ни газет, ни журналов»

первое, и второе, то неверно, что есть первое, или

неверно, что есть второе
~ (A & B) -> (~ A v ~ В)

или неверно, что есть второе, то неверно, что есть

первое и второе

( ~ A v ~ В) -> ~ (А & В)

Используя этот закон, от высказывания «Неверно, что изучение логики и трудно, и бесполезно» можно перейти к высказыванию «Изучение логики не является трудным, или же оно не бесполезно»

де Моргана связку «и» можно определить, используя отрицание, через

«или», и наоборот:
 «А и B» означает «неверно, что не A или не B »
(A & B) ≡ ~ (~ A v ~ B)

«А или В » означает «неверно, что не А и не В »
(A v В) ≡ ~ (~ А & ~B)

выражение: ~a→(a→b)
Например: «Если дважды два не равно четырем, то,

если дважды два всё-таки четыре, вся математика ничего не значит».

влечет любое высказывание
Если принимаются вместе высказывание и его отрицание,

то можно получить любое высказывание.
Из логического противоречия вытекает все что угодно
Формальное выражение: (a & ~a)→b

равно пяти, вытекает, что он, Рассел, — римский папа.

Отнимем

от обеих сторон равенства 2 + 2 = 5 по 3. Получим: 1=2. Если собеседник утверждает, что Рассел не является римским папой, то этот папа и Рассел — два разных лица. Но поскольку 1 = 2, папа и Рассел — одно и то же лицо.