- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Зміст
Содержание
- 2. Зміст1.Поняття вектора.2.Координати вектора.3.Абсолютна величина вектора.4.Рівні вектори.5.Колінеарні вектори.6.Компланарні вектори.7.Дії над векторами.8.Скалярний добуток векторів.9.Приклади.
- 3. Поняття вектораВектор - це величина, яка
- 4. Координати вектораКоординати вектора дорівнюють різниці координат його
- 5. Абсолютна величина вектора Абсолютна
- 6. Напрямленість векторівВектори і
- 7. Рівні векториРівні вектори – це вектори, що
- 8. Колінеарні векториКолінеарні вектори – це вектори, що лежать на паралельних прямих,або на одній прямій
- 9. Компланарні векториКомпланарні вектори - це вектори, що лежать у одній площині, абопаралельні одній площині
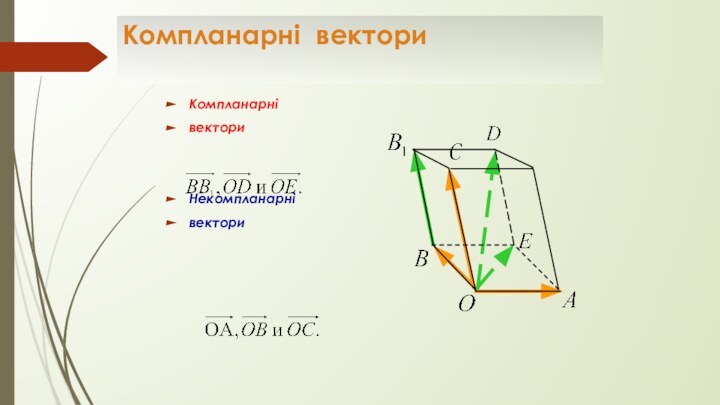
- 10. Компланарні векториКомпланарні векториНекомпланарні вектори
- 11. Дії над векторами Додавання (правило трикутника)Додавання( правило паралелограма)
- 12. Дії над векторамиДодавання (правило трикутника)За правилом трикутника
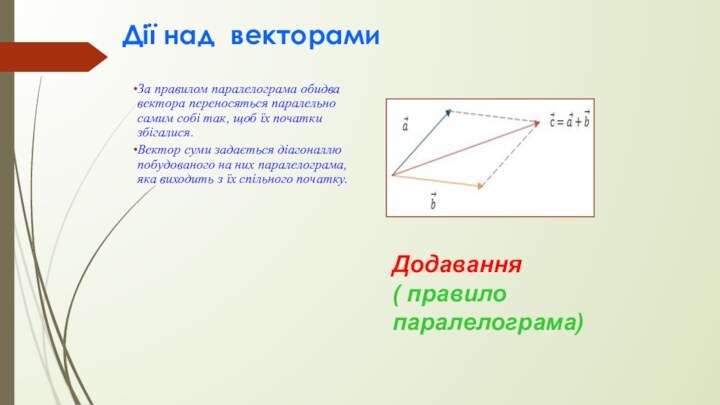
- 13. Дії над векторамиЗа правилом паралелограма обидва вектора
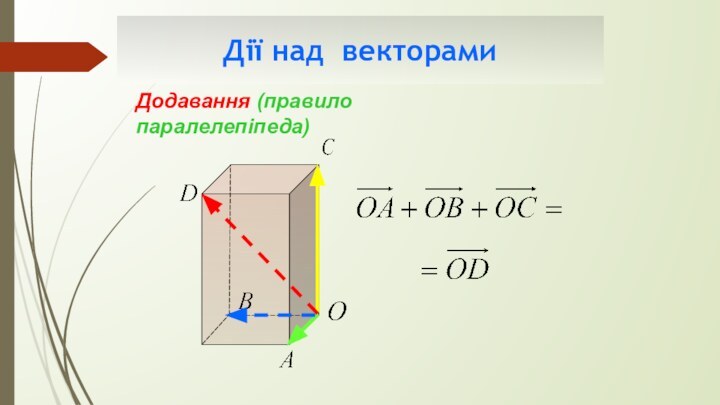
- 14. Дії над векторамиДодавання (правило паралелепіпеда)
- 15. Дії над векторамиДодаванняЗакони додавання:1) переставний2) сполучний
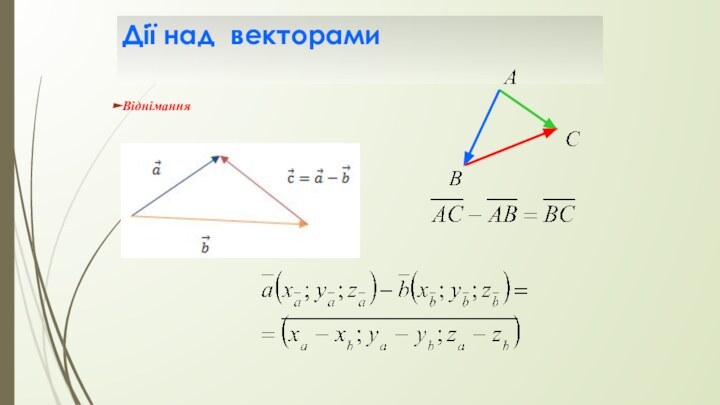
- 16. Дії над векторамиВіднімання
- 17. Дії над векторамиМноження вектора на числоЯкщо
- 18. Скалярний добуток векторівСкалярним добутком векторів називається сума
- 19. Скачать презентацию
- 20. Похожие презентации
Зміст1.Поняття вектора.2.Координати вектора.3.Абсолютна величина вектора.4.Рівні вектори.5.Колінеарні вектори.6.Компланарні вектори.7.Дії над векторами.8.Скалярний добуток векторів.9.Приклади.












Слайд 2
Зміст
1.Поняття вектора.
2.Координати вектора.
3.Абсолютна величина вектора.
4.Рівні вектори.
5.Колінеарні вектори.
6.Компланарні вектори.
7.Дії
над векторами.
Слайд 3
Поняття вектора
Вектор - це величина, яка характеризується
числовим значенням і напрямком.
Вектор - напрямлений відрізок.
Під направленим відрізком розуміють
впорядковану пару точок, перша з яких - точка A - називається його початком, а друга - B - його кінцем.
Слайд 4
Координати вектора
Координати вектора дорівнюють різниці координат його кінця
та початку
Координати вектора, для якого початком є початок координат
дорівнюють координатам його кінця
Слайд 5
Абсолютна величина
вектора
Абсолютна величина вектора
( модуль вектора, довжина вектора) дорівнює кореню квадратному
ізсуми квадратів його координат
Слайд 6
Напрямленість векторів
Вектори і
називають протилежно напрямленими, якщо протилежно напрямлені півпрямі AB і CD .
Вектори
і називають
співнапрямленими,
якщо співнапрямлені півпрямі AB і CD.
Слайд 7
Рівні вектори
Рівні вектори – це вектори, що мають
рівні абсолютні величини та однаковий напрям.
Рівні вектори – це
вектори, що мають рівні координати.
Слайд 8
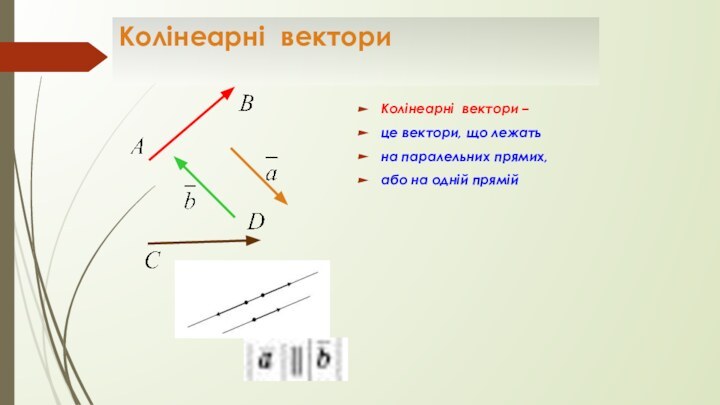
Колінеарні вектори
Колінеарні вектори –
це вектори, що лежать
на паралельних прямих,
або на одній прямій
Слайд 9
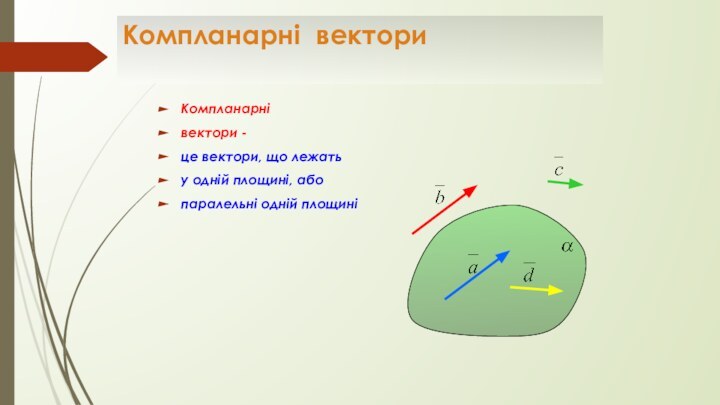
Компланарні вектори
Компланарні
вектори -
це вектори, що
лежать
у одній площині, або
паралельні одній площині
Слайд 12
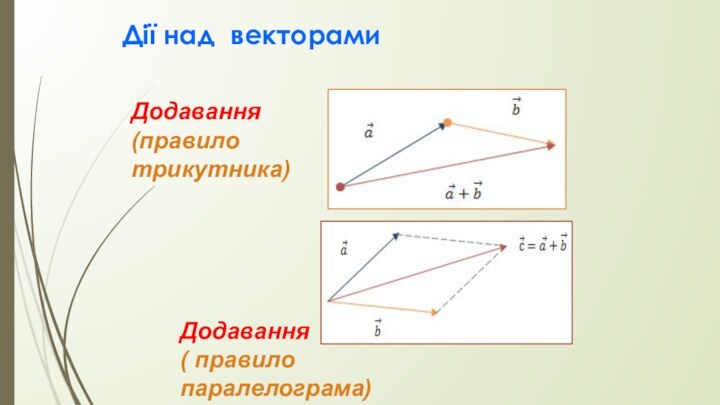
Дії над векторами
Додавання (правило трикутника)
За правилом трикутника обидва
вектора переносяться паралельно самим собі так, щоб початок одного
з них збігався з кінцем іншого.Вектор суми задається третьою стороною трикутника, що утворився, причому його початок збігається з початком першого вектора.
Слайд 13
Дії над векторами
За правилом паралелограма обидва вектора переносяться
паралельно самим собі так, щоб їх початки збігалися.
Вектор суми
задається діагоналлю побудованого на них паралелограма, яка виходить з їх спільного початку.Додавання
( правило паралелограма)
Слайд 17
Дії над векторами
Множення вектора на число
Якщо
, то координати векторів
пропорційні.І навпаки, якщо координати векторів пропорційні, то





























