Слайд 2
Абсолютные величины
Абсолютные величины – это величины, характеризующие абсолютные
размеры изучаемых статистикой процессов и явлений в конкретных условиях
места и времени.
В статистике различают два вида абсолютных величин:
Индивидуальные абсолютные величины характеризуют размеры признака у отдельных единиц совокупности, которые получают непосредственно в процессе статистического наблюдения, например, размер заработной платы отдельного работника и т.д.
Суммарные абсолютные величины характеризуют итоговую величину признака по определенной совокупности объектов, например, численность студентов г. Москвы.
Абсолютные статистические показатели всегда являются именованными числами и выражаются в натуральных единицах измерения.
Слайд 3
Натуральные единицы измерения
простые (тонны, килограммы, квадратные, кубические и
простые метры, мили, километры, галлоны, литры, миллилитры, декалитры (1дкл
= 10л), гектолитры (1гкл = 100л), штуки, караты и т.д.)
Слайд 8
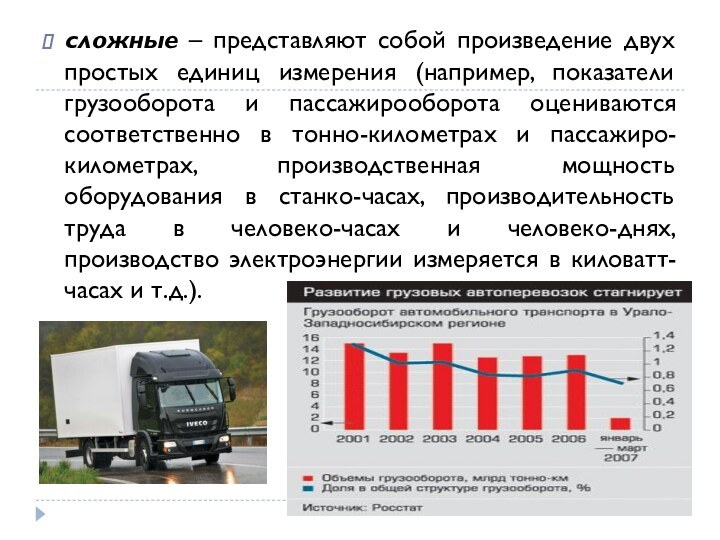
сложные – представляют собой произведение двух простых единиц
измерения (например, показатели грузооборота и пассажирооборота оцениваются соответственно в
тонно-километрах и пассажиро-километрах, производственная мощность оборудования в станко-часах, производительность труда в человеко-часах и человеко-днях, производство электроэнергии измеряется в киловатт-часах и т.д.).
Слайд 9
условно-натуральные измерители используются, когда какой-либо продукт имеет
несколько разновидностей и общий объем можно определить только исходя
из общего для всех потребительского свойства.
Например, мыло разных сортов переводят в условное мыло с 40%-м содержанием жирных кислот.
В консервной промышленности продукцию переводят в условные консервные банки массой 400 г, при этом 1000 усл. банок = 1 туб, 1 000 000 усл. банок = 1 муб.
Для измерения алкогольной продукции используют дал а/а – декалитры абсолютного алкоголя, т.е. спирта, практически не содержащего воды.
Слайд 10
Для определения объема продукции в условно-натуральных единицах измерения
(QУСЛ. НАТ.) следует объем продукции в натуральных единицах измерения
(Qнат) умножить на коэффициент пересчета (Кпересч):
QУСЛ. НАТ. = QНАТ * КПЕРЕСЧ,
где коэффициент пересчета определяется отношением
Слайд 11
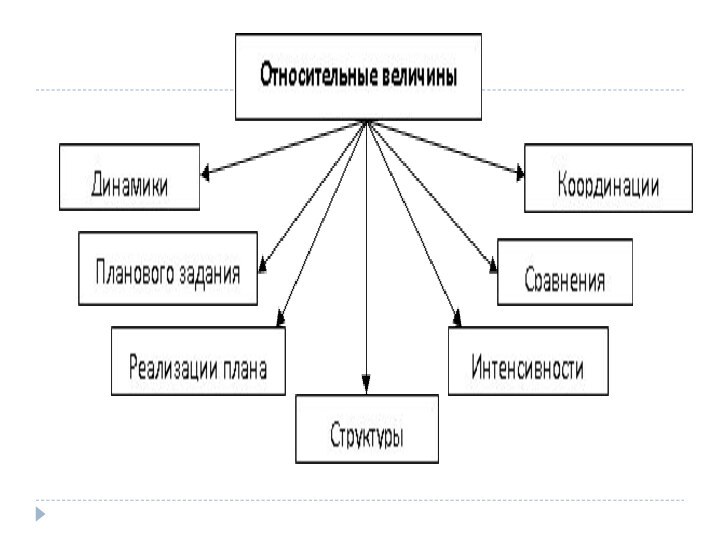
Относительные показатели
Относительный показатель – это обобщающий показатель, который
представляет собой результат деления одного абсолютного показателя на другой
и выражает соотношение между количественными характеристиками социально-экономических процессов и явлений:
текущий/ сравниваемый показатель
основание / базисный /база сравнения
Относительные показатели могут выражаться в коэффициентах, процентах, промилле(0/00) , продецимилле (0/000) или быть именованными числами.
Если база сравнения принимается за 1, то относительный показатель выражается в коэффициентах, если база принимается за 100, 1000 или 10 000, то относительный показатель соответственно выражается в процентах, промилле и продецимилле.
Слайд 13
1. Относительный показатель планового задания
2. Относительный показатель реализации
плана
рассчитывается как отношение уровня, запланированного на будущий период (yпл),
к уровню, фактически сложившемуся в прошлом (y0):
определяется как отношение фактически достигнутого уровня в текущем периоде (y1) к запланированному на этот же период (yпл):
Слайд 14
3. Относительный показатель динамики
представляет собой отношение текущего уровня
исследуемого явления (y1) к уровню этого же явления в
прошлом (y0):
Между относительными показателями планового задания, реализации плана и динамики существует следующая взаимосвязь:
ОППЗ ОПРП = ОПД
Слайд 15
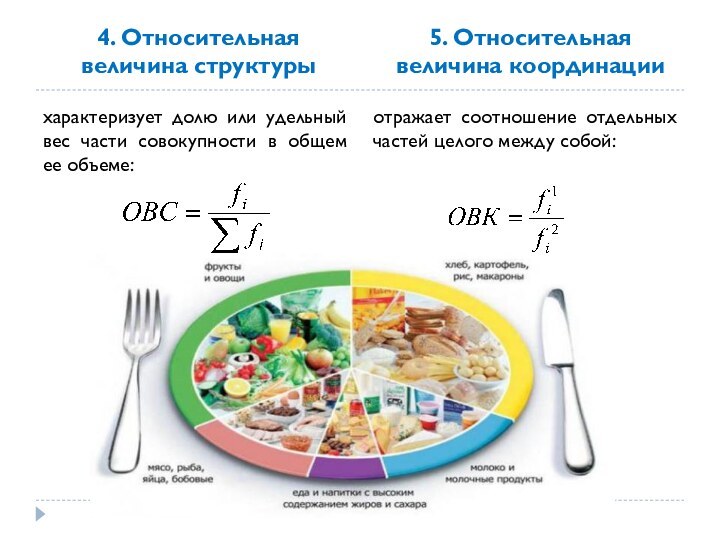
4. Относительная величина структуры
5. Относительная величина координации
характеризует долю
или удельный вес части совокупности в общем ее объеме:
отражает
соотношение отдельных частей целого между собой:
Слайд 16
6. Относительный показатель интенсивности
7. Относительный показатель сравнения
всегда является
именованной величиной и характеризует степень распространения изучаемого процесса или
явления в присущей ему среде:
представляет собой соотношение одноименных абсолютных показателей, характеризующих разные объекты, но относящиеся к одному и тому же моменту времени:
Слайд 17
Средняя величина – это обобщающий показатель, характеризующий типичный
уровень варьирующего признака в расчете на единицу однородной совокупности
в конкретных условиях места и времени.
Средняя величина является как бы абстрактной в том смысле, что среди индивидуальных значений признака может не встретится ни одного значения, равного по величине его среднему.
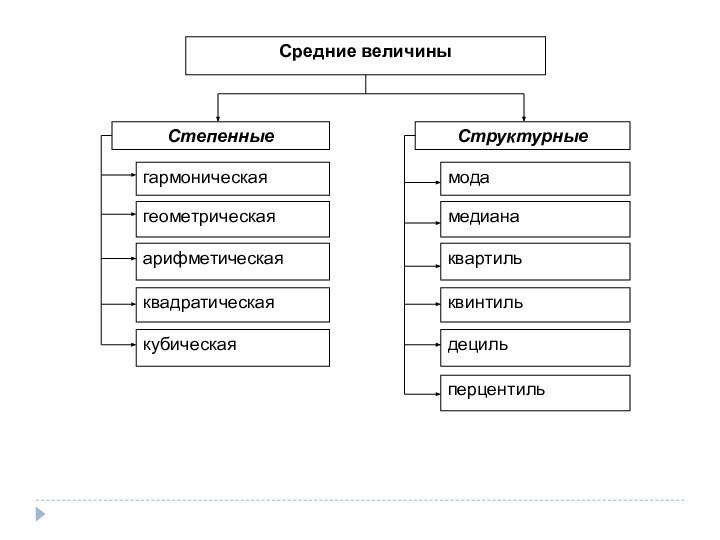
Средние величины
Слайд 18
Средняя величина всегда именованная, она имеет ту же
единицу измерения, что и признак у отдельных единиц совокупности.
Слайд 20
Степенные средние
Степенные средние – это обобщающие показатели центра
распределения исследуемых данных или центральной тенденции данных при нормальной
форме распределения. Формулы расчета степенных средних имеют общий показатель степени m. В зависимости от того, какое значение принимает показатель степени в формулах расчета, различают несколько видов степенных средних.
Слайд 21
Простая средняя вычисляется по несгруппированным данным, а взвешенная
средняя вычисляется по сгруппированным данным.
Правило мажорантности средних:
Если рассчитать
все виды средних для одних и тех же исходных данных, то их значения окажутся неодинаковыми, т. к. чем больше показатель степени m, тем больше средняя величина:
Слайд 22
Пример применения средней арифметической величины
Требуется найти среднюю выработку
одного рабочего за смену в бригаде из 15 человек,
если известно, сколько деталей изготовил каждый из них.
Выработка рабочих за смену в бригаде
Так как данные не сгруппированы, то рассчитаем среднюю выработку по формуле средней арифметической простой:
Теперь сгруппируем данные и рассчитаем среднюю выработку рабочего за смену по формуле средней арифметической взвешенной:
Слайд 23
Ряд распределения рабочих по выработке деталей за смену
Слайд 24
Пример применения средней гармонической величины
Средняя гармоническая простая применяется
в тех случаях, когда требуется исчислить среднюю из величин,
обратно пропорциональных изучаемому явлению, т.е. из относительных величин.
Пример. Изготовлено три детали. На изготовление первой детали рабочий тратит 2,3 чел.-часа, второй - 2,5 чел.-часа, третьей - 3,1 чел.-часа. Определить, каковы средние затраты времени на одну деталь (трудоемкость):
Средняя гармоническая взвешенная применяется в тех случаях, когда известны варианты (х) и объемы признаков (w=xf), а частоты (f) не известны. Например, для определения средней заработной платы работников достаточно знать фонд заработной платы (w) и зарплату сотрудников разных категорий (x).
Слайд 25
Основное применение геометрическая средняя находит при определении средних
коэффициентов роста
Например, в результате инфляции за первый год цена
товара возросла в 2 раза к предыдущему году, а за второй год еще в 3 раза к уровню предыдущего года. Арифметическая средняя здесь непригодна, ибо если за год цены возросли бы в (2+3)/2 = 2,5 раза, то за два года цена возросла бы в 2,5*2,5 = 6,25 раза. Геометрическая средняя дает правильный ответ:
Слайд 26
Структурные средние
Структурные средние применяются для изучения внутреннего строения
и структуры рядов распределения значений признака. Они являются дополнительными
характеристиками к степенным средним.
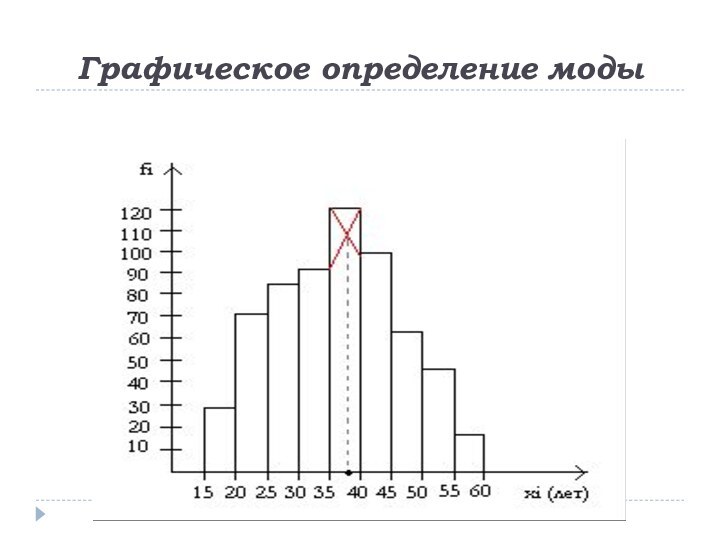
Наиболее распространенными среди них являются мода и медиана.
Мо = 25
Мо1 = 47, Мо2 = 52
Мода в данном ряду отсутствует.
Слайд 27
В интервальных рядах распределения с равными интервалами мода
определяется по формуле:
где xMo начальное значение модального интервала;
i
– величина модального интервала;
fMo частота модального интервала;
fMo-1 частота интервала, предшествующего модальному;
fMo+1 частота интервала, следующего за модальным.
Слайд 28
Медиана – величина признака, которая делит упорядоченную последовательность
его значений на две равные по численности части.
Иначе можно
сказать, что медиана это серединное значение ранжированного вариационного ряда.
В дискретном вариационном ряду распределения определение медианы сводится к определению номера медианной единицы ряда по формуле:
где n – число изучаемых единиц.
Слайд 29
В интервальном вариационном ряду медиана определяется по формуле:
где
xMe начальное значение интервала, содержащего медиану;
i величина
медианного интервала;
f сумма частот ряда;
SMe-1 сумма накопленных частот, предшествующих медианному интервалу;
fMe частота медианного интервала.
Слайд 31
Графическое изображение медианы
Слайд 32
Правило определения формы распределения данных с помощью характеристик
центральной тенденции ряда
Если форма распределения данных нормальная (симметричная), то
значения средней величины, медианы и моды равны между собой:
Если распределение по форме близко к нормальному закону распределения, то медиана находится между модой и средней величиной, причем ближе к средней, чем к моде.
Если имеет место левосторонняя асимметрия, то значение средней величины меньше моды, т.е. большая часть единиц совокупности имеет значение признака ниже модального:
̅х < Ме < Мо.
Если имеет место правосторонняя асимметрия, то значение средней величины больше моды, т.е. большая часть единиц совокупности имеет значение признака выше модального:
̅х > Ме > Мо.
Слайд 33
К структурным характеристикам исследуемой совокупности относятся также:
кварти́ли (от
лат. quata - четверть) - варианты, делящие совокупность на
4 равные части,
квинти́ли (от лат. quinque - пять) - варианты, делящие совокупность на 5 равных частей;
деци́ли (от лат. decem - десять) - варианты, делящие совокупность на 10 частей,
перценти́ли (от англ. per cent – из расчета на сто) - варианты, делящие совокупность на 100 частей.
Слайд 34
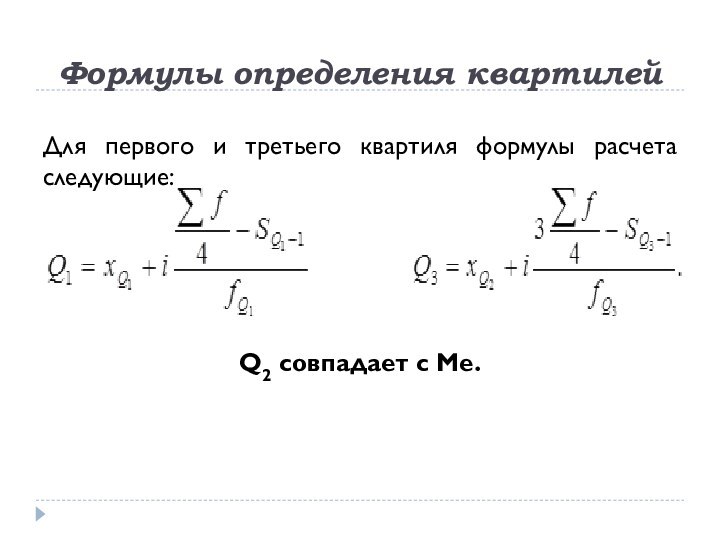
Формулы определения квартилей
Для первого и третьего квартиля формулы
расчета следующие:
Q2
совпадает с Ме.