Презентация на тему Зубчатые передачи

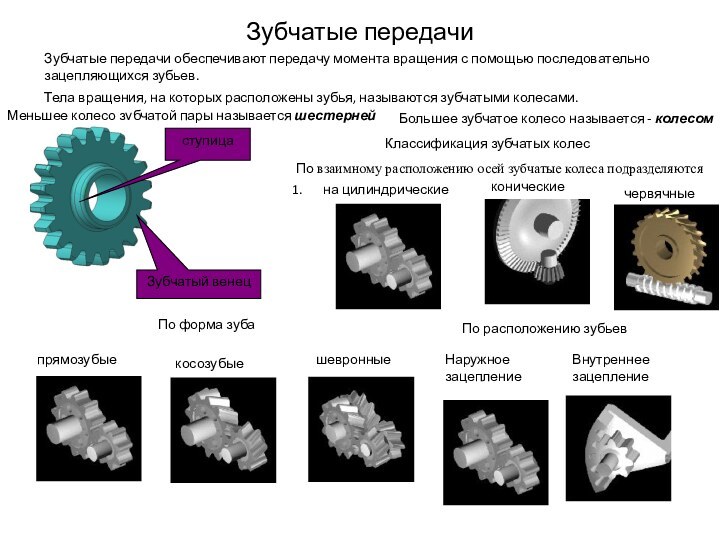
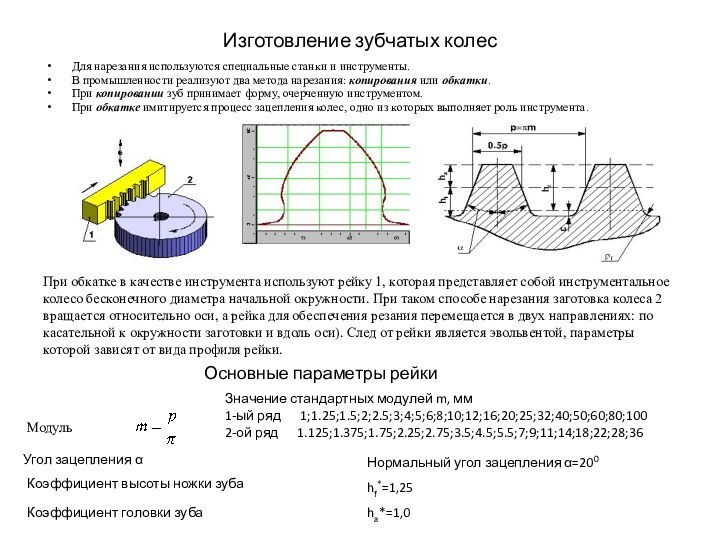
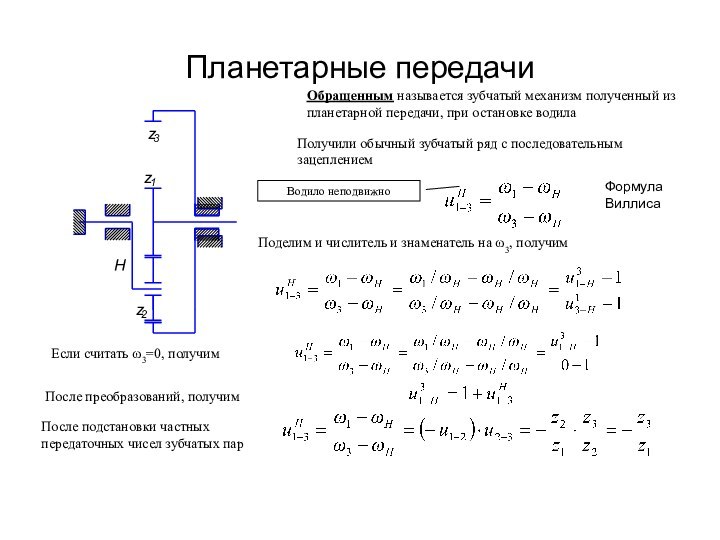
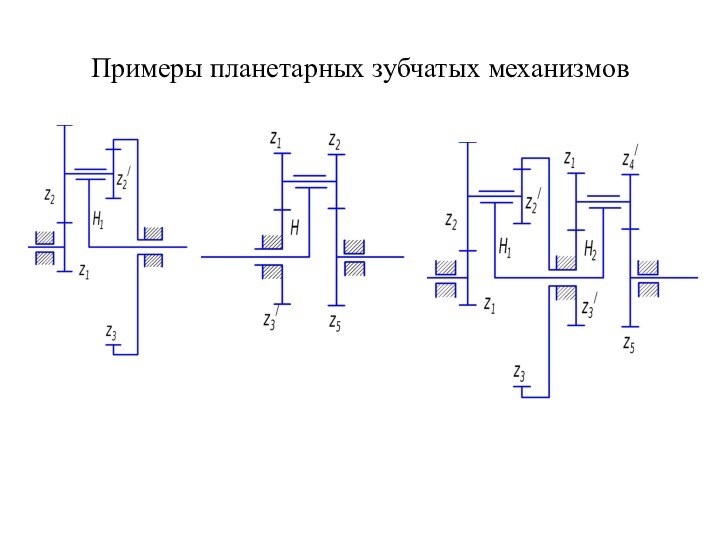
Эвольвента (или инволюта) окружности представляет собой кривую, центры кривизны

Эвольвента окружности может быть получена как траектория точки прямой, перекатывающейся без скольжения по этой окружности диаметром d0 , называемой основной окружностью.

А1

А2

А3

Эвольвента

Основная окружность

Точка пересечения общей нормали к эвольвентам с межосевой линией называется полюсом зацепления Р

Положение нормали к поверхности определяется углом W (т.е. углом между линией зацепления и нормалью к линии центров), который называется углом зацепления.

инструменты.
В промышленности реализуют два метода нарезания: копирования или обкатки.

При обкатке в качестве инструмента используют рейку 1, которая представляет собой инструментальное колесо бесконечного диаметра начальной окружности. При таком способе нарезания заготовка колеса 2 вращается относительно оси, а рейка для обеспечения резания перемещается в двух направлениях: по касательной к окружности заготовки и вдоль оси). След от рейки является эвольвентой, параметры которой зависят от вида профиля рейки.

Значение стандартных модулей m, мм
1-ый ряд 1;1.25;1.5;2;2.5;3;4;5;6;8;10;12;16;20;25;32;40;50;60;80;100
2-ой ряд 1.125;1.375;1.75;2.25;2.75;3.5;4.5;5.5;7;9;11;14;18;22;28;36

Модуль

Основные параметры рейки

Угол зацепления 

Нормальный угол зацепления =200

Коэффициент высоты ножки зуба

hf*=1,25

Коэффициент головки зуба

ha*=1,0

окружность колеса является касательной к средней линии контура инструмента,

Диаметр делительной окружности

Диаметр вершин зубьев

Диаметр впадин зубьев

Межосевое расстояние

Передачи со смещением (смещение положительное). При нарезании со смещением диаметр начальной окружности не касается средней линии контура инструментальной рейки. Смещение рейки позволяет избежать подреза ножки зуба при изготовлении колес с малым числом зубьев и увеличить прочностные характеристики зубьев, но ведет к заострению вершины зубьев

Отрицательное смещение рейки усиливает подрезание ножки зуба уменьшает прочностные

Формулы для определения геометрических размеров передач идентичны

Делительный диаметр

Диаметр вершин зубьев

Диаметр впадин зубьев

механизм называется приводом. Чаще всего привод представляет собой ряды

Механизм, состоящий из одной или нескольких пар зубчатых колес, размещенных в корпусе, и предназначенный для уменьшения частоты вращения, называется редуктором

Механизм, состоящий из одной или нескольких пар зубчатых колес, размещенных в корпусе, и служащий для увеличения частоты вращения называется - мультипликатором

Отношение угловых скоростей на входе 1 и выходе 2 кинематической цепи называется передаточным отношением u

Перемножим полученные выражения

Для простой зубчатой передачи:
(частное передаточное отношение)

Для случая кратного зацепления можно записать

Запишем передаточное число каждой передачи

Общее передаточное отношение последовательного ряда зубчатых колес равно произведению частных передаточных отношений

зубчатых колес равно дроби у которой в числителе стоит

Передаточные числа выраженные через геометрические параметры передач

Передаточное число кратного зубчатого ряда, выраженное через геометрические параметры передач

Для случая последовательного ряда с паразитными шестернями

Перемножая полученные выражения получим

Частные передаточные отношения

Передаточное отношение выраженное через геометрические параметры передач

Размеры и числа зубьев промежуточных шестерен не влияют на общее передаточное отношение

колес
Водило
Солнечное колесо
Планетное колесо
Зубчатое колесо с подвижной осью называется планетным

Зубчатое колесо относительно которого вращается сателлит называется солнечным или центральным колесом

Рычаг с помощью которого перемещаются оси сателлитов называется водило

Планетарные передачи получили широкое распространение в авиации и приборостроении благодаря компактности, большим интервалам изменения передаточных чисел

Движение можно передать от центрального колеса к водилу и в обратном направлении

Указывает неподвижный элемент передачи

Передаточное отношение передачи

Движение передается от центрального колеса 1 на водило

передачи, при остановке водила
Получили обычный зубчатый ряд с последовательным

Водило неподвижно

После подстановки частных передаточных чисел зубчатых пар

Формула Виллиса

Поделим и числитель и знаменатель на 3, получим

Если считать 3=0, получим

После преобразований, получим

h
a
c
f
0