- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии теорема Косинусов
Содержание
- 2. Цели урокаНайти способ находить стороны и углы треугольников по трем известным элементамДоказать теорему косинусов
- 3. Теорема косинусовКвадрат стороны треугольника равен сумме квадратов
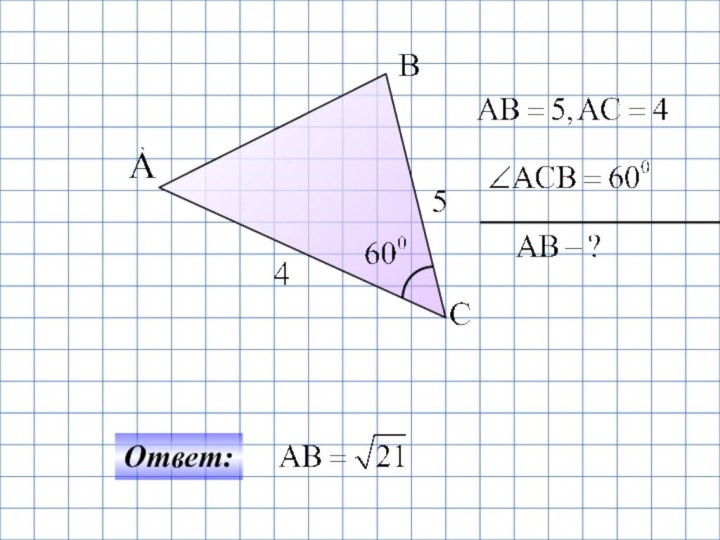
- 4. Запишите теорему косинусов для треугольников:∆АВС∆ VXR∆ POH∆ UTR
- 5. Выразим косинус угла из теоремы косинусов
- 6. Что можно находить по этой формуле?угол (или косинус угла) треугольника по трем известным сторонам
- 7. Какую задачу можно решать, используя теорему косинусов?Какое количество элементов должно быть известно, чтобы задача была решена?
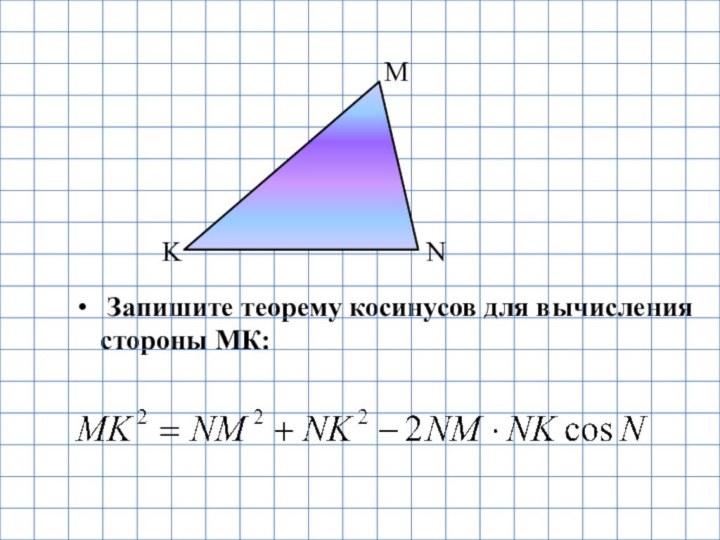
- 8. Запишите теорему косинусов для вычисления стороны МК:MNK
- 9. Ответ:
- 10. Задача о футболисте.Футбольный мяч находится в точке
- 11. Математическая модель задачи найдем угол А, равный
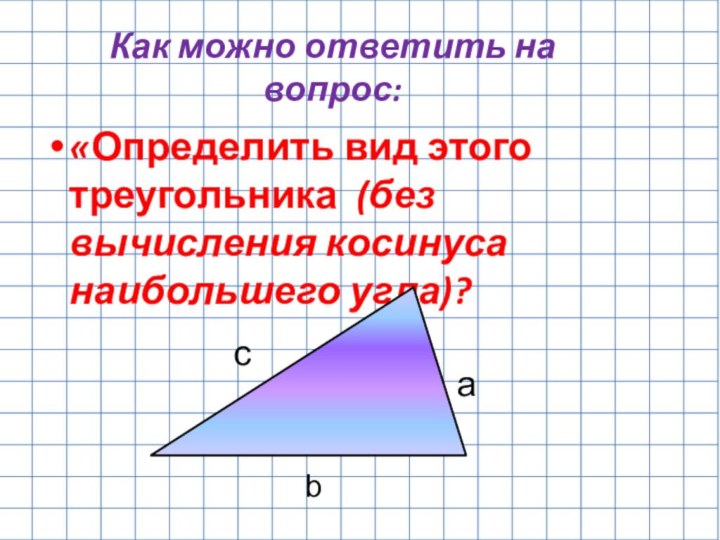
- 12. Как можно ответить на вопрос: «Определить вид этого треугольника (без вычисления косинуса наибольшего угла)?саb
- 13. Как можно ответить на вопрос: «Определить
- 14. Скачать презентацию
- 15. Похожие презентации
Цели урокаНайти способ находить стороны и углы треугольников по трем известным элементамДоказать теорему косинусов











Слайд 3
Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух
других сторон минус удвоенное произведение этих сторон на косинус
угла между ними.А
С
В
Слайд 6
Что можно находить по этой формуле?
угол (или
косинус угла) треугольника по трем известным сторонам
Слайд 7
Какую задачу можно решать, используя
теорему косинусов?
Какое количество
элементов должно быть известно, чтобы задача была решена?
Слайд 10
Задача о футболисте.
Футбольный мяч находится в точке А
футбольного поля на расстояниях 23 м и 24 м
от оснований В и С стоек ворот.Футболист направляет мяч в ворота. Найдите угол α попадания мяча в ворота, если ширина ворот равна 7 м.
Слайд 11
Математическая модель задачи
найдем угол А, равный α.
По
теореме косинусов определим cos A
Угол α находим по таблице:
α ≈ 1657