- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Логарифмы
Содержание
- 2. НАУЧИТЬСЯ ПРИМЕНЯТЬ ОПРЕДЕЛЕНИЕ ЛОГАРИФМА И СВОЙСТВА ЛОГАРИФМОВ ПРИ ВЫПОЛНЕНИИ ПРАКТИЧЕСКИХ ЗАДАНИЙЦЕЛЬ УРОКА
- 3. « СЧИТАЙ
- 4. ЗНАНИЯ1.Продолжить текст: «Логарифмом числа в по
- 5. ПОНИМАНИЕ
- 6. ПРИМЕНЕНИЕ 1. Вычислить Log5
- 7. ОТВЕТЫ1) 32) 23) 274) 3; - 45) 3
- 8. АНАЛИЗ Найти значение выражения: 2.Сравнить значения выражения: 9 и
- 9. ОТВЕТЫ ¼
- 10. ОПРЕДЕЛЕНИЕ ЛОГАРИФМАLog√3 X = 4Log32 sinπ/4 = ХLogх 8 = 3
- 11. ОТВЕТЫ 9 - 0,1 3
- 12. ПРАВИЛА И СВОЙСТВА ЛОГАРИФМОВLog3 (2х - 1)
- 13. ОТВЕТЫ5arctg9+πk1; 4.1; - 1/3
- 14. Решение уравнений на основании определения логарифма, например,
- 15. ВЫЧИСЛИТЬ: Log 2 16;
- 16. СРАВНИТЕ СО СВОИМИ ОТВЕТАМИ !
- 17. ВЫЧИСЛИТЕ: 3 log 3 18;
- 18. СРАВНИТЕ СО СВОИМИ ОТВЕТАМИ !
- 19. Спасибо за урок!
- 20. НЕМНОГО ИСТОРИИ Потому-то, словно пена Опадают
- 21. ЛОГАРИФМИЧЕСКАЯ ЛИНЕЙКАЧерез 10 лет после появления логарифмических
- 22. Затем логарифмическую линейку вытеснили калькуляторы. Но без
- 23. В математике логарифмическая спираль впервые упоминается в 1638 году Рене Декартом.
- 24. ЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ В ПРИРОДЕОдин из наиболее распространенных
- 25. ЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ В ПРИРОДЕХищные птицы кружат над
- 26. ПРИМЕНЕНИЕ ЛОГАРИФМОВмузыкаТак называемые ступени темперированной хроматической гаммы
- 27. ЗВЕЗДЫ, ШУМ И ЛОГАРИФМЫ Громкость шума и яркость звезд оцениваются одинаковым образом – по логарифмической шкале.
- 28. ПСИХОЛОГИЯ Изучая логарифмы, ученые пришли к
- 29. Скачать презентацию
- 30. Похожие презентации
НАУЧИТЬСЯ ПРИМЕНЯТЬ ОПРЕДЕЛЕНИЕ ЛОГАРИФМА И СВОЙСТВА ЛОГАРИФМОВ ПРИ ВЫПОЛНЕНИИ ПРАКТИЧЕСКИХ ЗАДАНИЙЦЕЛЬ УРОКА


























Слайд 2 НАУЧИТЬСЯ ПРИМЕНЯТЬ ОПРЕДЕЛЕНИЕ ЛОГАРИФМА И СВОЙСТВА ЛОГАРИФМОВ ПРИ
ВЫПОЛНЕНИИ ПРАКТИЧЕСКИХ ЗАДАНИЙ
Слайд 3 « СЧИТАЙ НЕСЧАСТНЫМ ТОТ ДЕНЬ ИЛИ ЧАС, В
КОТОРЫЙ ТЫ НЕ УСВОИЛ НИЧЕГО НОВОГО И НИЧЕГО НЕ
ПРИБАВИЛ К СВОЕМУ ОБРАЗОВАНИЮ.» Я. А. КОМЕНСКИЙ.
Слайд 4
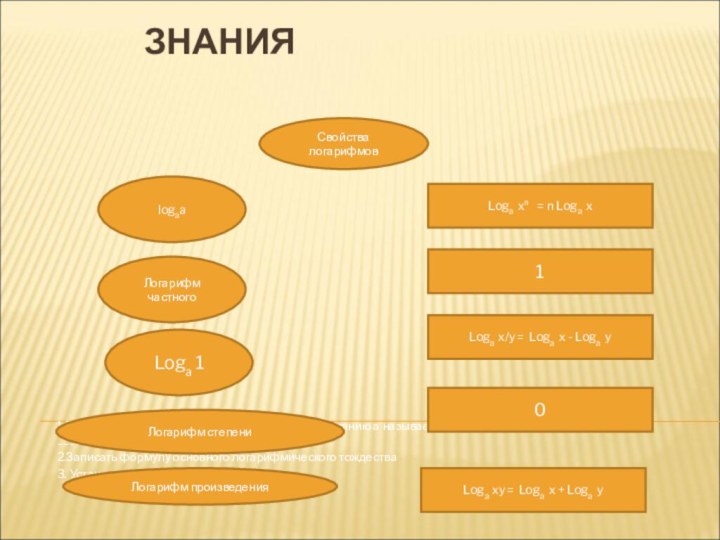
ЗНАНИЯ
1.Продолжить текст: «Логарифмом числа в по основанию
а называется _____________, ____________________________»
2.Записать формулу основного логарифмического тождества
3. Установить
соответствие:
Слайд 6
ПРИМЕНЕНИЕ
1. Вычислить Log5 125
2. Пользуясь основным
логарифмическим тождеством, вычислить 1.7 3. Используя свойства логарифмов выполнить
задание : Log3 X+ Log3 3 =4 4. Вычислить :lg1000; lg0.0001 5. Вычислить: ln e3
Слайд 12
ПРАВИЛА И СВОЙСТВА ЛОГАРИФМОВ
Log3 (2х - 1) =
2
Log2 Log3 (tgX) = 1
6 Log3 Х - 12Log3
Х = 0(3х – 5х-2) Log3 (5 - 4х) =0
Слайд 14
Решение уравнений на основании определения логарифма, например, уравнение
loga х = б (а > 0, а≠ 1,
б>0 ) имеет решение х = аb.Метод потенцирования. Под потенцированием понимается переход от равенства, содержащего логарифмы, к равенству, не содержащему их: если , loga f(х) = loga g(х), то f(х) = g(х), f(х)>0, g(х)>0 , а > 0, а≠ 1.
Метод введение новой переменной.
Метод логарифмирования обеих частей уравнения.
Метод приведения логарифмов к одному и тому же основанию.
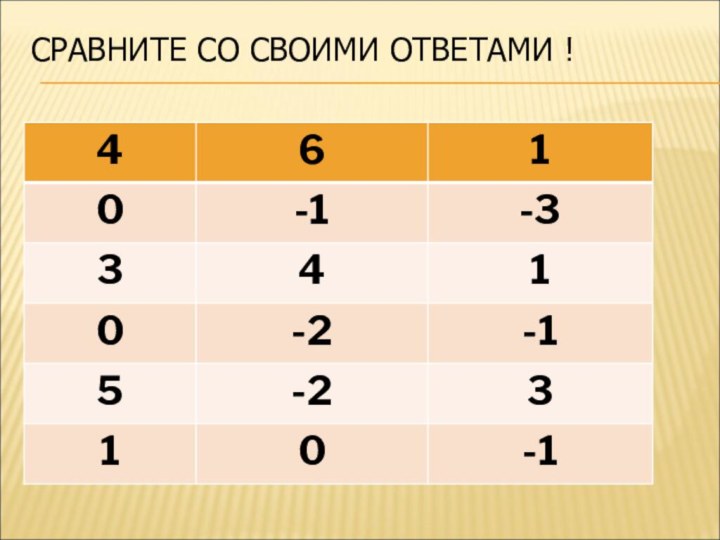
Слайд 15
ВЫЧИСЛИТЬ:
Log 2 16;
log 2 64;
log 2 2;Log 2 1 ; log 2 (1/2); log 2 (1/8);
Log 3 27; log 3 81; log 3 3;
Log 3 1; log 3 (1/9); log 3 (1/3);
Log1/2 1/32; log1/2 4; log0,5 0,125;
Log0/5 (1/2); log0,5 1; log1/2 2.
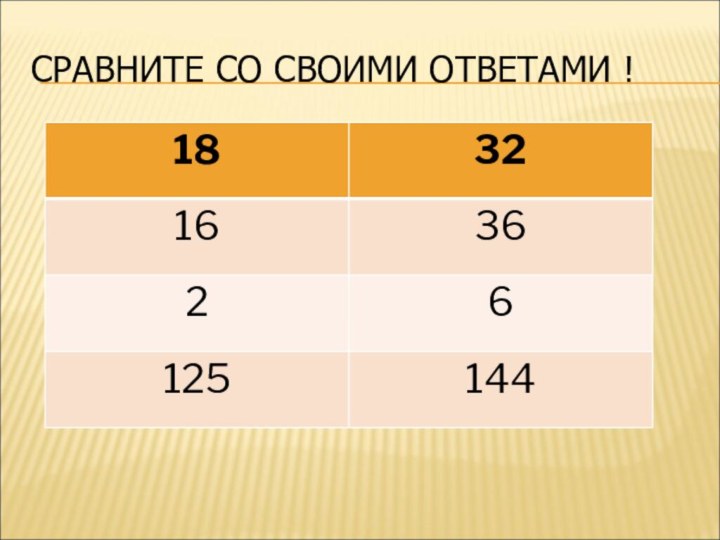
Слайд 17
ВЫЧИСЛИТЕ:
3 log 3 18;
3 5log 3 2;
5 log 5 16; 0,3 2log 0,3 6;
10 log 10 2; (1/4) log(1/4) 6;
8 log 2 5; 9 log 3 12.
Слайд 20
НЕМНОГО ИСТОРИИ
Потому-то, словно пена
Опадают наши рифмы
И
величие степенно
Отступает в логарифмы.
Борис Слуцкий
Первый изобретатель логарифмов — шотландский
барон Джон Непер (1550—1617)
Слайд 21
ЛОГАРИФМИЧЕСКАЯ ЛИНЕЙКА
Через 10 лет после появления логарифмических таблиц
английский математик Д .Гунтер изобрел логарифмическую линейку.
И ещё
недавно трудно было представить инженера без логарифмической линейки в кармане.
Слайд 22
Затем логарифмическую линейку вытеснили калькуляторы.
Но без логарифмической
линейки не были бы построены ни первые компьютеры ,
ни калькуляторы.





























