Слайд 2
Задача 1
B 8 № 27485.
Прямая
y = 7x – 5 параллельна касательной к графику
функции y = x2 + 6x - 8. Найдите абсциссу точки касания.
Решение.
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой y = 7x – 5 угловые коэффициенты касательной и прямой равны. Поэтому абсцисса точки касания находится из уравнения : y’ = 7.
(y = x2 + 6x – 8)’ = 7;
2x + 6 = 7;
2x = 1; x = 0,5.
Ответ: 0,5.
Слайд 3
Задача 2
B 8 № 27486.
Прямая y
= -4x – 11 является касательной к графику функции
f(x) = x3 + 7x2 + 7x - 6. Найдите абсциссу точки касания.
Решение. Условие касания графика функции y = f(x) и прямой y = kx + b задаётся системой требований:
Слайд 4
Получим
Проверка подстановкой показывает,
что первый корень не удовлетворяет, а второй удовлетворяет уравнению
(*). Поэтому искомая абсцисса точки касания (−1).
Ответ: −1.
Слайд 5
Задача 3
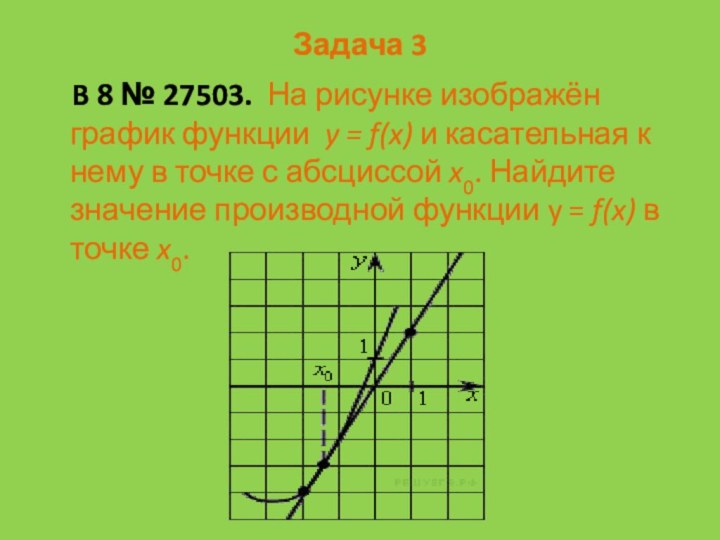
B 8 № 27503. На рисунке изображён график
функции y = f(x) и касательная к нему в
точке с абсциссой x0. Найдите значение производной функции y = f(x) в точке x0.
Слайд 6
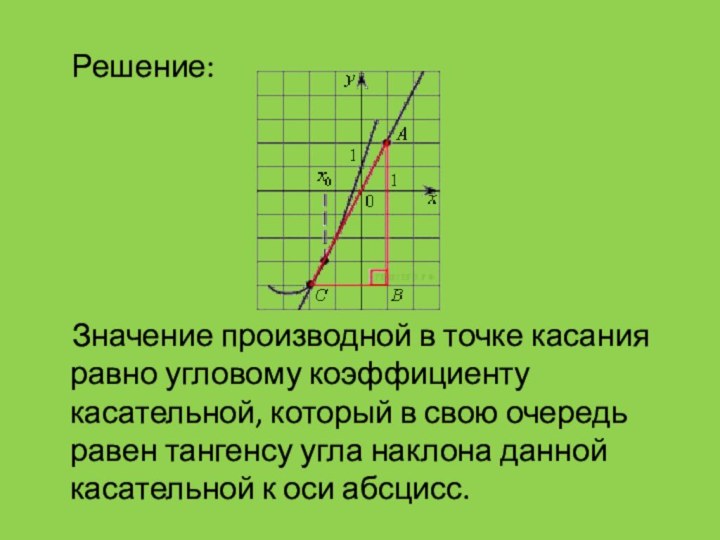
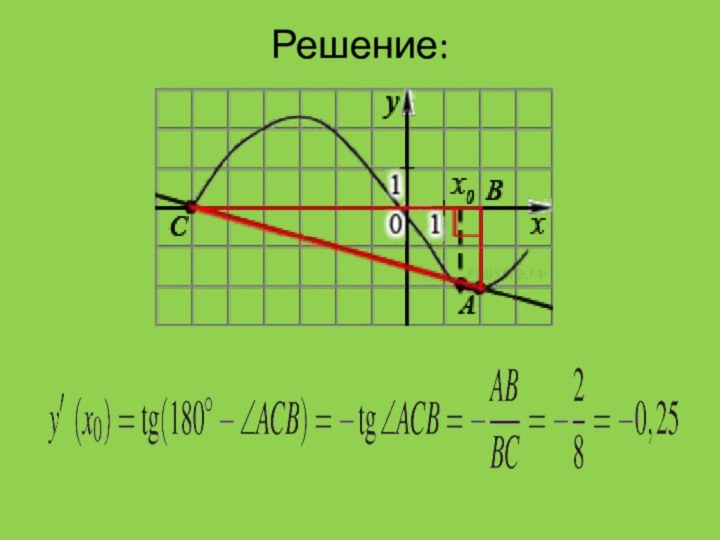
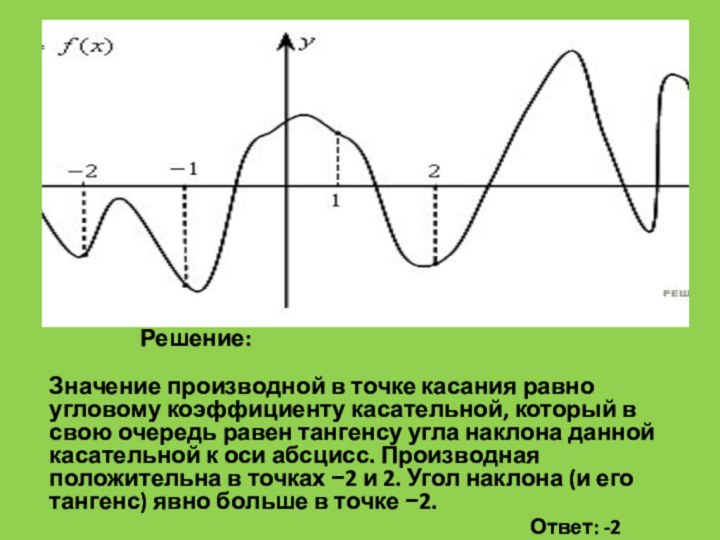
Решение:
Значение производной в точке
касания равно угловому коэффициенту касательной, который в свою очередь
равен тангенсу угла наклона данной касательной к оси абсцисс.
Слайд 7
Углом наклона касательной является угол ACB
прямоугольного треугольника ABC, у которого A(1;2), B(1;-4), C(-2;-4).
Ответ: 2
Слайд 8
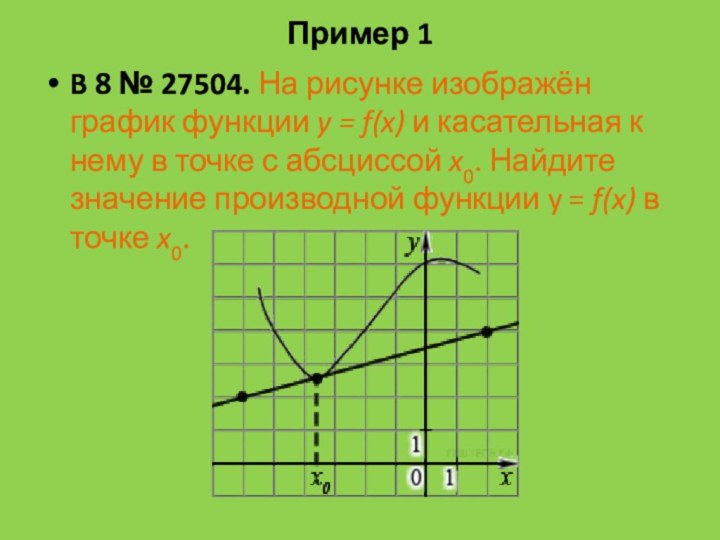
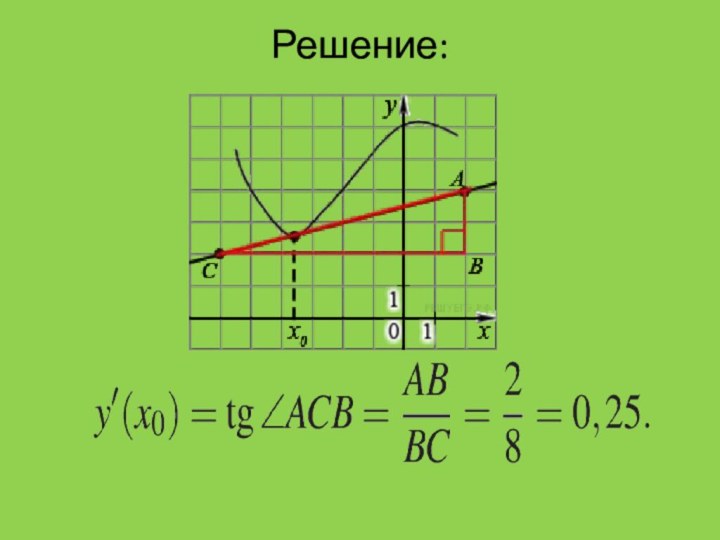
Пример 1
B 8 № 27504. На рисунке изображён график функции y
= f(x) и касательная к нему в точке с
абсциссой x0. Найдите значение производной функции y = f(x) в точке x0.
Слайд 10
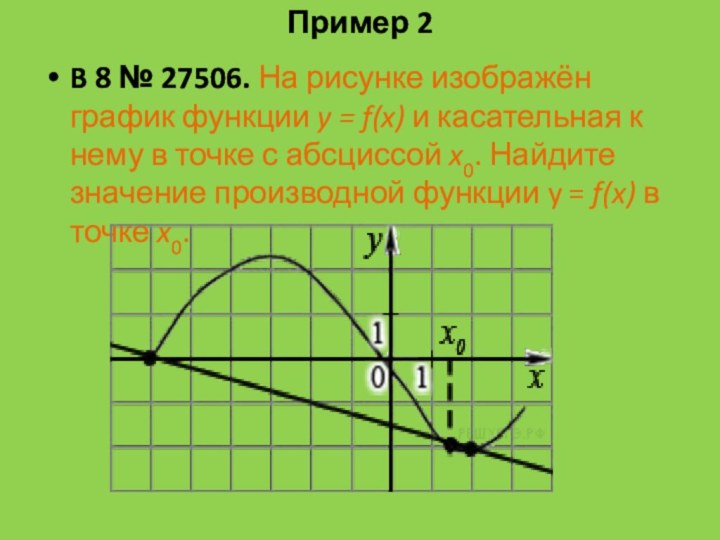
Пример 2
B 8 № 27506. На рисунке изображён график функции y
= f(x) и касательная к нему в точке с
абсциссой x0. Найдите значение производной функции y = f(x) в точке x0.
Слайд 12
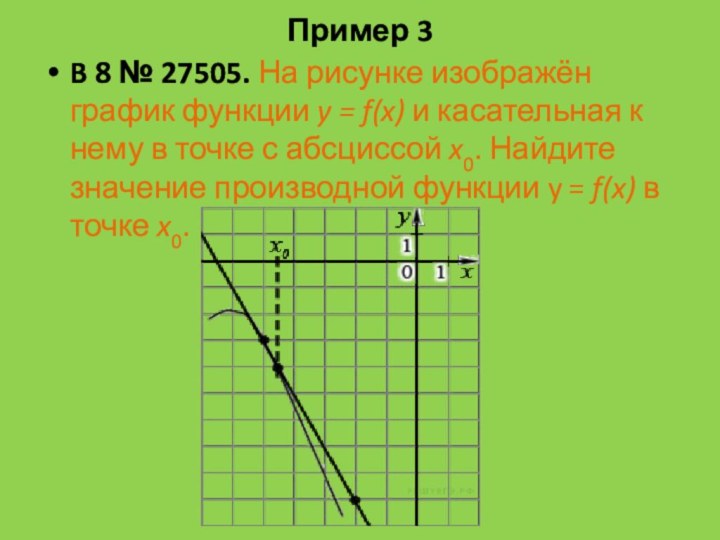
Пример 3
B 8 № 27505. На рисунке изображён график функции y
= f(x) и касательная к нему в точке с
абсциссой x0. Найдите значение производной функции y = f(x) в точке x0.
Слайд 14
Задача 4
B 8 № 40129.
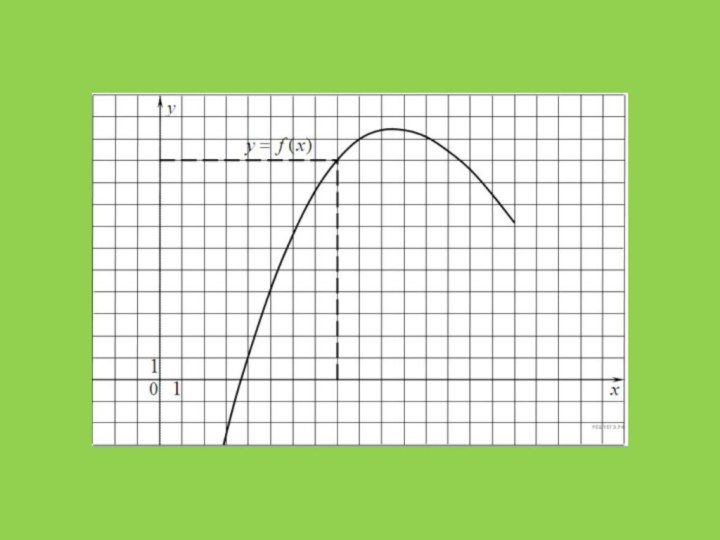
На рисунке изображен
график функции
y = f(x). Прямая, проходящая через
начало координат, касается графика этой функции в точке с абсциссой 8. Найдите f'(8).
Слайд 17
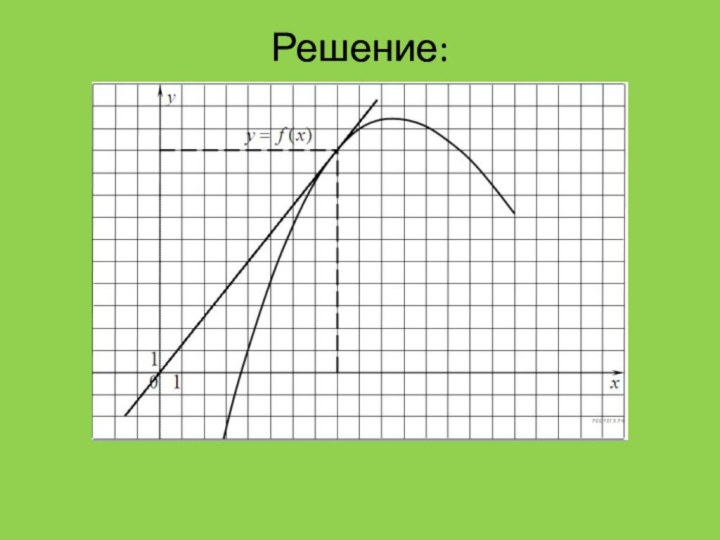
Поскольку касательная проходит через
начало координат, ее уравнение имеет вид y = kx. Эта прямая
проходит через точку
(8; 10), поэтому 10 = 8 · k, откуда k = 1,25. Поскольку угловой коэффициент касательной равен значению производной в точке касания, получаем: f'(8) = 1,25.
Ответ: 1,25.
Слайд 18
Задача 5
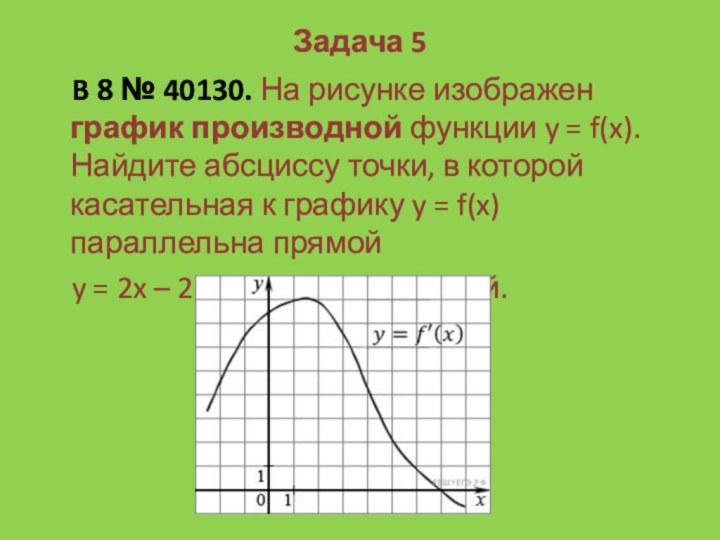
B 8 № 40130. На рисунке изображен график
производной функции y = f(x). Найдите абсциссу точки, в
которой касательная к графику y = f(x) параллельна прямой
y = 2x – 2 или совпадает с ней.
Слайд 19
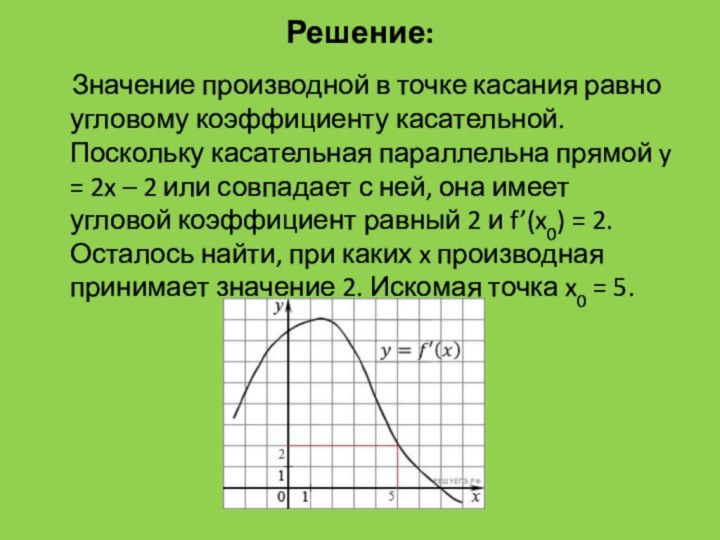
Решение:
Значение производной в точке касания равно
угловому коэффициенту касательной. Поскольку касательная параллельна прямой y =
2x – 2 или совпадает с ней, она имеет угловой коэффициент равный 2 и f’(x0) = 2. Осталось найти, при каких x производная принимает значение 2. Искомая точка x0 = 5.
Слайд 20
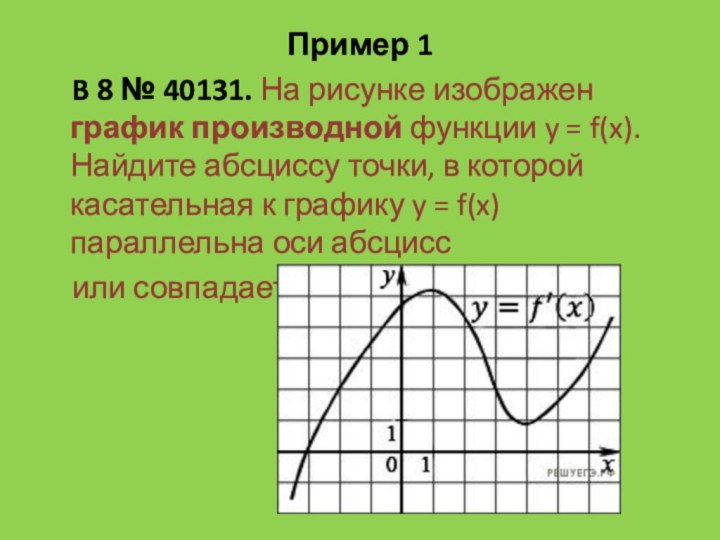
Пример 1
B 8 № 40131. На рисунке изображен график
производной функции y = f(x). Найдите абсциссу точки, в
которой касательная к графику y = f(x) параллельна оси абсцисс
или совпадает с ней.
Слайд 21
Решение:
Значение производной в точке касания равно
угловому коэффициенту касательной. Поскольку касательная параллельна оси абсцисс или
совпадает с ней, она имеет вид y = b, и её угловой коэффициент равен 0. Следовательно, мы ищем точку, в которой угловой коэффициент, равен нулю, а значит, и производная равна нулю. Производная равна нулю в той точке, в которой её график пересекает ось абсцисс. Поэтому иcкомая точка x = -3. Ответ: -3
Слайд 22
Задача 6
B 8 № 119972. Прямая y = 3x
+ 1 является касательной к графику функции
f(x) = ax2 + 2x + 3. Найдите a.
Решение.
Прямая y = kx + b является касательной к графику функции y = f(x) в точке x0
тогда и только тогда, когда одновременно
f(x0) = y(x0) и f’(x0) = k.
Слайд 23
Получим
Искомое значение
а равно 0,125.
Ответ: 0,125
Слайд 24
Пример 1
B 8 № 119973. Прямая y = -5x
+ 8 является касательной к графику функции
f(x) = 28x2 + bx + 15. Найдите b, учитывая, что абсцисса точки касания больше 0.
Решение.
Условие касания графика функции y = f(x) и прямой y = kx + l задаётся системой требований:
Слайд 25
В нашем случае имеем:
По условию абсцисса точки касания положительна, поэтому x =
0,5, откуда
b = −33.
Ответ: -33
Слайд 26
Пример 2
B 8 № 119974. Прямая y = 3x
+ 4 является касательной к графику функции
f(x)
= 3x2 – 3x + c. Найдите c.
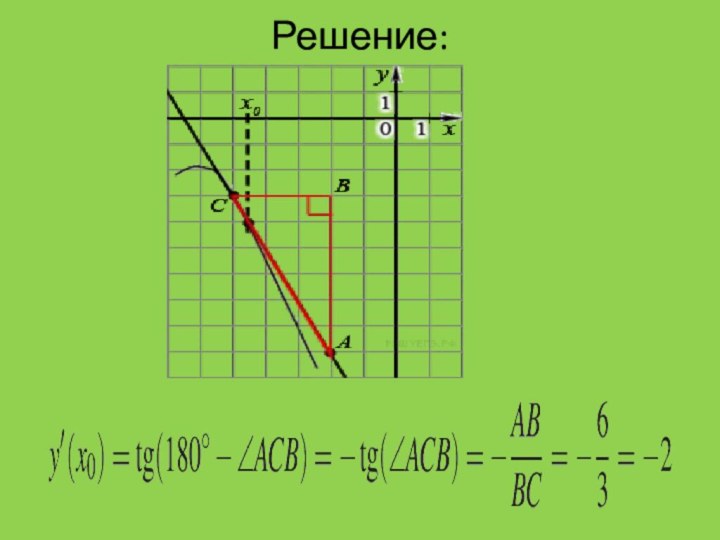
Решение:
условие касания графика функции и прямой задаётся системой требований:
Ответ: 7.
Слайд 27
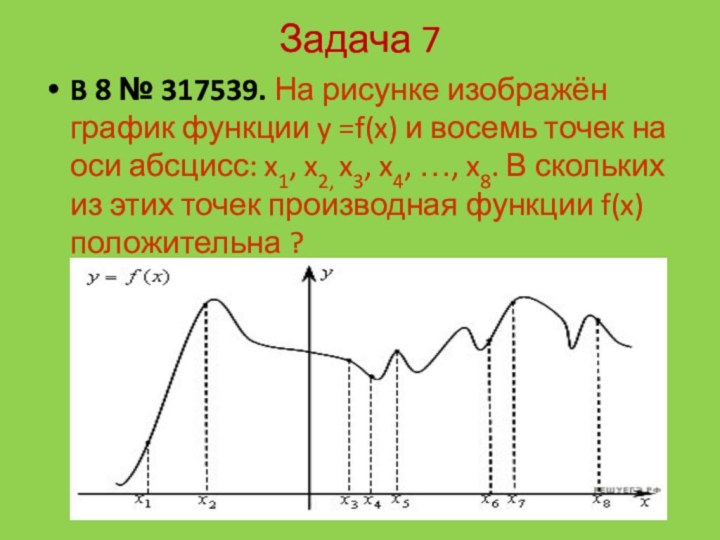
Задача 7
B 8 № 317539. На рисунке изображён график функции y
=f(x) и восемь точек на оси абсцисс: x1, x2,
x3, x4, …, x8. В скольких из этих точек производная функции f(x) положительна ?
Слайд 28
Решение:
Положительным значениям производной соответствуют интервалы, на
которых функция возрастает. На них лежат точки
x1, x2, x6, x7. Таких точек 4.
(Или: положительным значениям производной соответствуют те точки графика функции, в которых угол наклона касательной острый.)
Ответ:4.
Слайд 29
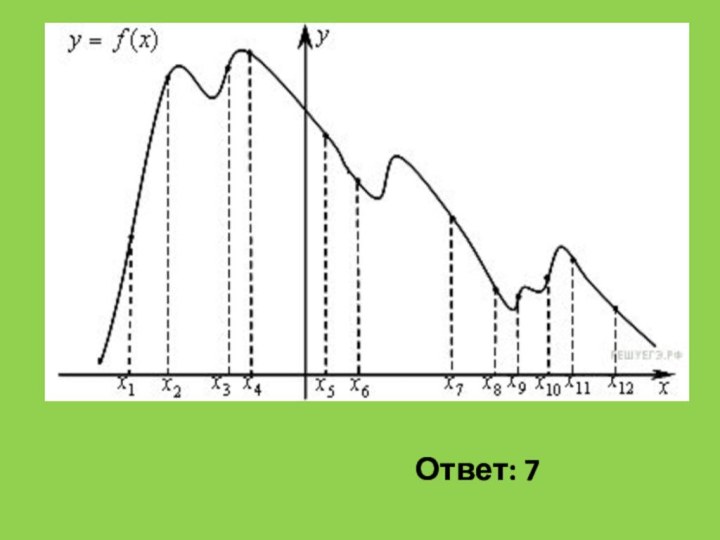
Пример 1
B 8 № 317540. На рисунке изображён график функции y
=f(x) и двенадцать точек на оси абсцисс: x1, x2,
x3, …, x12.
В скольких из этих точек производная функции f(x) отрицательна?
Слайд 31
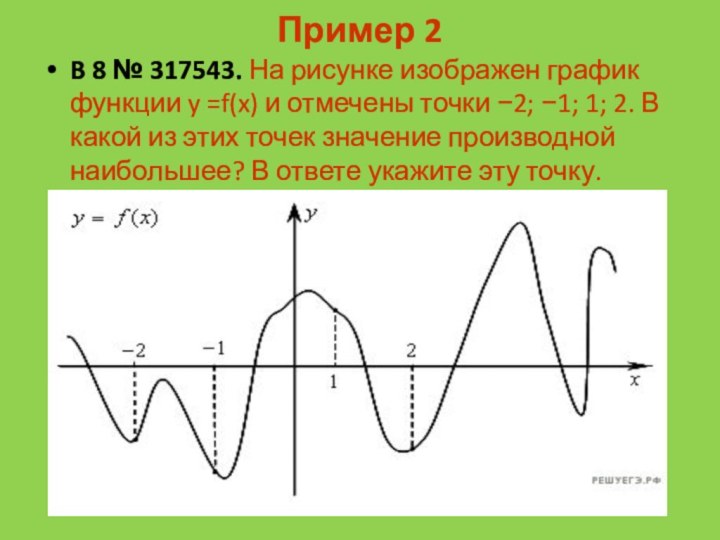
Пример 2
B 8 № 317543. На рисунке изображен график функции y
=f(x) и отмечены точки −2; −1; 1; 2. В
какой из этих точек значение производной наибольшее? В ответе укажите эту точку.