- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему и конспект урока алгебры в 7 классе Возведение в квадрат суммы и разности двух выражений
Содержание
- 2. «Лучший способ изучить что-либо – это открыть самому».Дьёрдь Пойа
- 3. Сформулируйте правило умножения степеней.Сформулируйте правило возведения степени
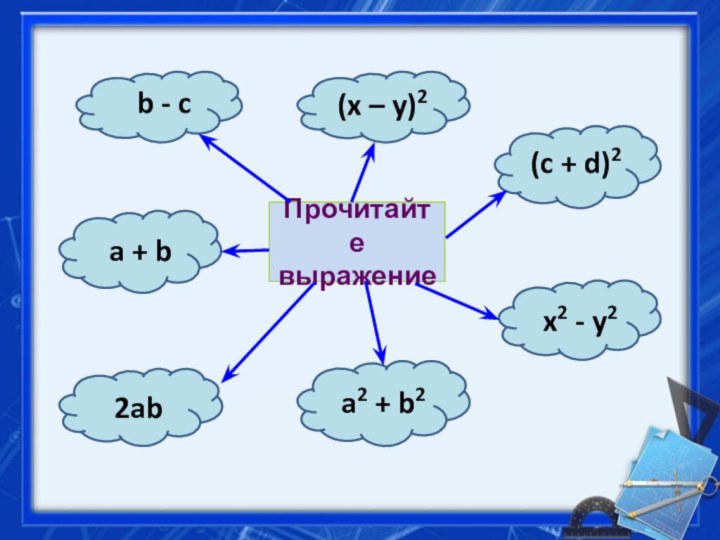
- 4. Прочитайте выражениеb - ca + b2ab(x – y)2(c + d)2a2 + b2x2 - y2
- 5. 1. Найдите квадраты выражений: 6; а;
- 6. (а + b)2 = (а + b)(а
- 7. Формулы сокращенного умноженияТема урока: «Возведение в квадрат суммы и разности двух выражений»
- 8. Алгоритм применения формул(а + b)2 = а2
- 9. (а + b)2 = а2 + 2аb
- 10. Заполните таблицу№ВыражениеКвадрат 1выраженияУдвоенное произведение 1 и 2
- 11. Самостоятельная работаПреобразуйте в многочлен:а) (4 + b)2
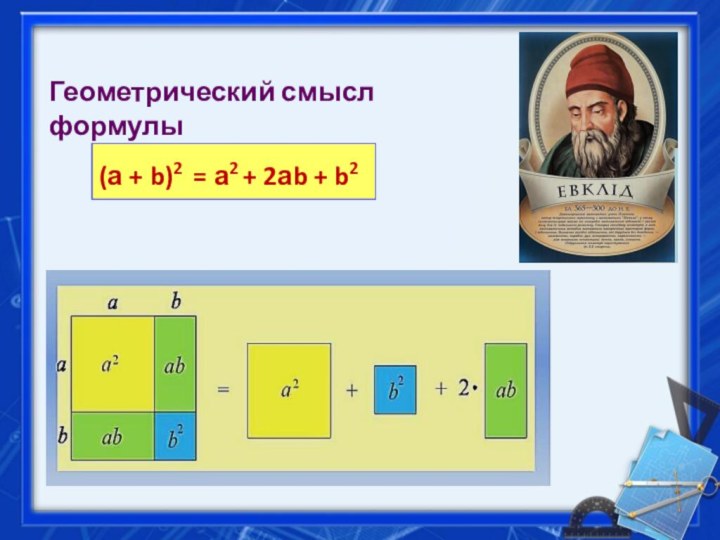
- 12. Геометрический смысл формулы(а + b)2 = а2 + 2аb + b2
- 13. Подведение итогов урокаС какими формулами вы познакомились
- 14. Домашнее заданиеУчебник: п. 32 (прочитать, выучить правила
- 15. Скачать презентацию
- 16. Похожие презентации
«Лучший способ изучить что-либо – это открыть самому».Дьёрдь Пойа












Слайд 3
Сформулируйте правило умножения степеней.
Сформулируйте правило возведения степени в
степень.
Сформулируйте правило возведения произведения в степень.
Сформулируйте правило умножения одночлена
на одночлен?Сформулируйте правило умножения многочлен на многочлен?
Повторение изученного материала
Слайд 5
1. Найдите квадраты выражений:
6; а; -4;
3b; 5x2y3; -7cy4
2. Найдите удвоенное произведение:
c и d; 2x и 3у; 3m и -4m2; 6a и 5b3. Представьте в виде многочлена выражение:
а) (х + 3)(х – 7)
б) (2у – 4)(х + 5)
в) (а + b)2
г) (2х + 7)(х + 3)
д) (а – b)2
Слайд 6 (а + b)2 = (а + b)(а +
b) =
= а2 +
аb + аb + b2 = а2 + 2аb + b2 (а – b)2 = (а – b)(а – b) =
= а2 – аb – аb + b2 = а2 – 2аb + b2
Слайд 7
Формулы сокращенного умножения
Тема урока: «Возведение в квадрат
суммы
и разности двух выражений»
Слайд 8
Алгоритм применения формул
(а + b)2 = а2 +
2аb + b2
1. Найти квадрат первого выражения
2. Определить
знак перед удвоенным произведением (по знаку в скобках)
3. Найти удвоенное произведение первого и второго
выражений
4. Найти квадрат второго выражения
Слайд 9 (а + b)2 = а2 + 2аb +
b2
(а – b)2 = а2 – 2аb +
b2 Квадрат суммы двух
выражений равен
квадрату первого выражения
плюс удвоенное произведение
первого и второго выражений
плюс квадрат
второго выражения
Квадрат разности двух
выражений равен
квадрату первого выражения
минус удвоенное произведение
первого и второго выражений
плюс квадрат
второго выражения
Слайд 10
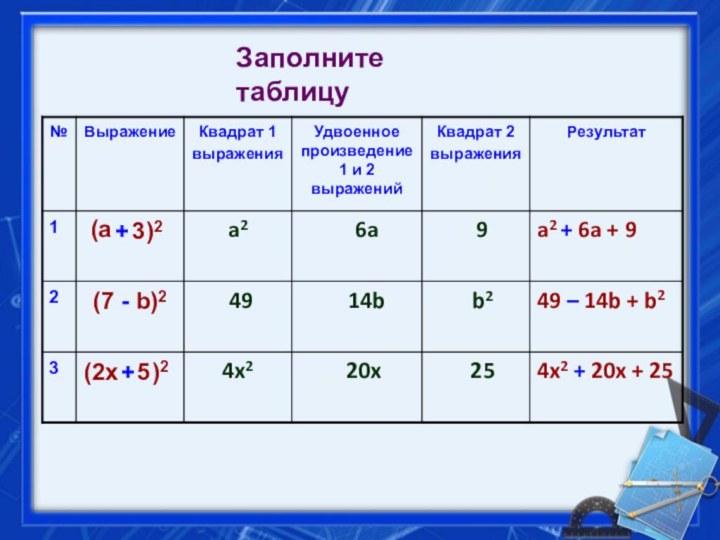
Заполните таблицу
№
Выражение
Квадрат 1
выражения
Удвоенное
произведение
1 и 2
выражений
Квадрат
2
выражения
Результат
1
(а
+
3)
2
a
2
6a
9
a
2
+
6a + 9
2
(7
-
b
)
2
49
14b
b
2
49
–
14b + b
2
3
(2
x
+
5
)
2
4x
2
20x
25
4x
2
+
20x + 25
Слайд 11
Самостоятельная работа
Преобразуйте в многочлен:
а) (4 + b)2
б)
(а – 0,2)2
в) (х + 3у)2
г) (5а
– 2b)2 д) (0,3х + у)2
Слайд 13
Подведение итогов урока
С какими формулами вы познакомились сегодня
на уроке?
Почему эти формулы называются формулами сокращенного умножения?
Чему равен квадрат суммы двух выражений?
Чему равен квадрат разности двух выражений?
Добились ли вы поставленной перед собой цели?
Слайд 14
Домашнее задание
Учебник: п. 32 (прочитать, выучить правила и
№ 800, 804, 801.