- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к уроку алгебры на тему Числовые функции
Содержание
- 2. Цели
- 3. ПланАктуальность формирования понятия «функция»Различные подходы к введению
- 5. Термин «функция» возник лишь в 1664 году
- 6. Функцией называют такую зависимостьпеременной у от переменной
- 8. Способы задания функции
- 9. Область определения функцииОбластью определения функции называют множество
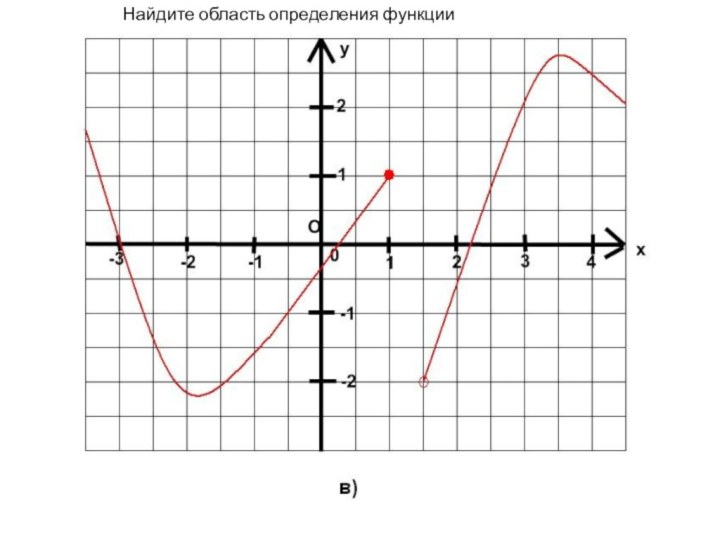
- 10. Найдите область определения функции
- 11. Область значений функцииОбластью значений функции называют множество
- 12. Найдите область значений функции
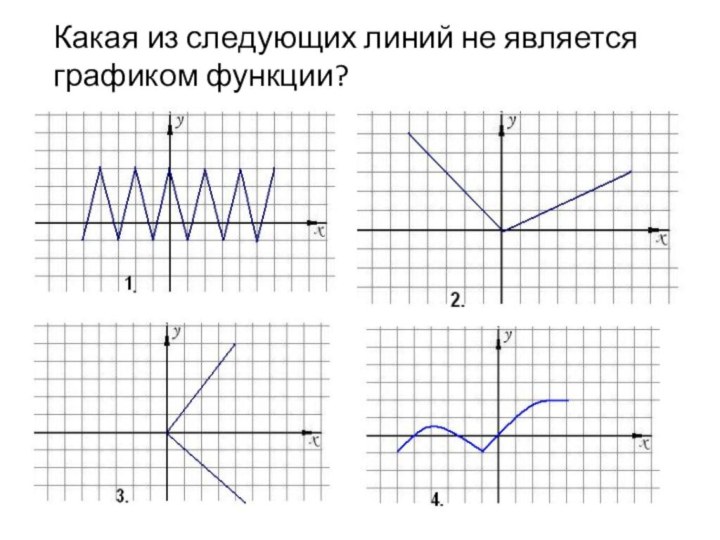
- 13. Графиком функции называется множество всех точек координатной
- 14. «Прикладное значение понятий функции огромно. В нем,
- 15. Рейсовый автобус проделал путь из города А
- 16. Устная работа
- 17. Функция
- 19.
- 20. Устная работа
- 21. 1.График функции y = x3 + 1
- 22. Область определения функцииD(f)=(-∞;+∞)D(f)=(∞;-1)U(-1;∞)2х-6≥0 ⇒ 2х≥6 ⇒ х≥3D(f)=[3;+∞)
- 23. у=х-2Графики функций изученных ранее:
- 24. Скачать презентацию
- 25. Похожие презентации
Цели и задачи: 1. Обратить внимание на проблемы, связанные с формированием понятия «Функция». 2. Рассмотреть различные подходы к введению понятия. 3. Поделиться опытом в решении проблем, связанных с формированием представлений












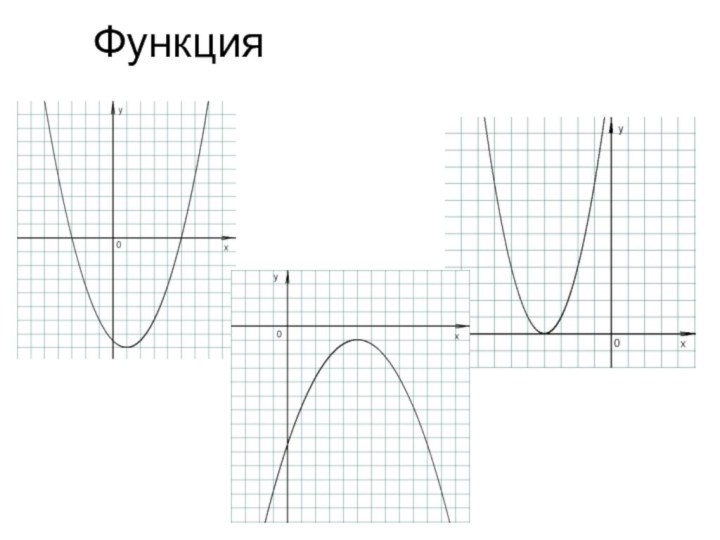


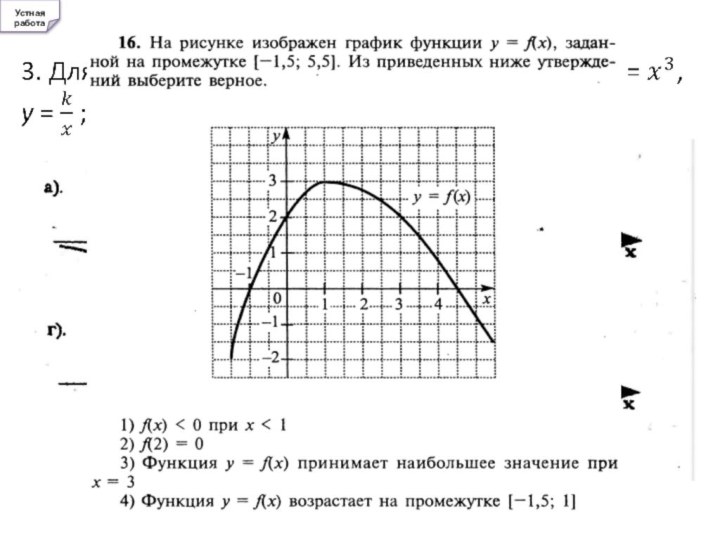




Слайд 3
План
Актуальность формирования понятия «функция»
Различные подходы к введению понятия
в школьном курсе математики
Введение понятия «функция» по УМК А.Г.
МордковичаМои наработки в решении поставленной проблемы
Полученные результаты
Выводы
Слайд 5 Термин «функция» возник лишь в 1664 году в
работах немецкого ученого Лейбница, только его ученик Бернулли в
1718 году дал определение функции, свободное от геометрических образов. Леонард Эйлер определяет функцию так: «Величины, зависящие от других так, что с изменением вторых меняются и первые, называется функцией».Обозначая функцию, мы пользуемся знаком f. Этот символ изобрел в 1733 году французский математик Клеро.
Слайд 6
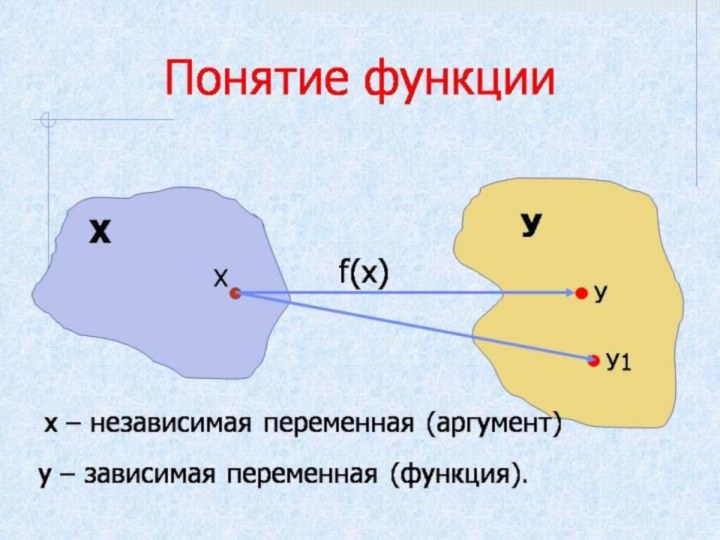
Функцией называют такую зависимость
переменной у от переменной х,
при которой каждому значению
переменной х соответствует единственное
значение
у.Обозначение: f(x), g(x) …
х – независимая переменная (аргумент)
у – зависимая переменная (функция)
Слайд 9
Область определения функции
Областью определения функции называют множество всех
значений, которые принимает независимая переменная (х)
Обозначение: D(y), D(f)
(от латинского
domain - область)
Слайд 11
Область значений функции
Областью значений функции называют множество всех
значений , которые принимает зависимая переменная (у)
Обозначение: E(y), Е(f)
(от латинского equal - равно)Слайд 13 Графиком функции называется множество всех точек координатной плоскости,
абсциссы которых равны значениям аргумента, а ординаты-соответствующим значениям функции
Слайд 14 «Прикладное значение понятий функции огромно. В нем, как
в «зародыше», уже заложена вся идея овладения явлениями природы
и процессами техники с помощью математического аппарата», - писал советский математик А.Я. Хинчин.
Слайд 15
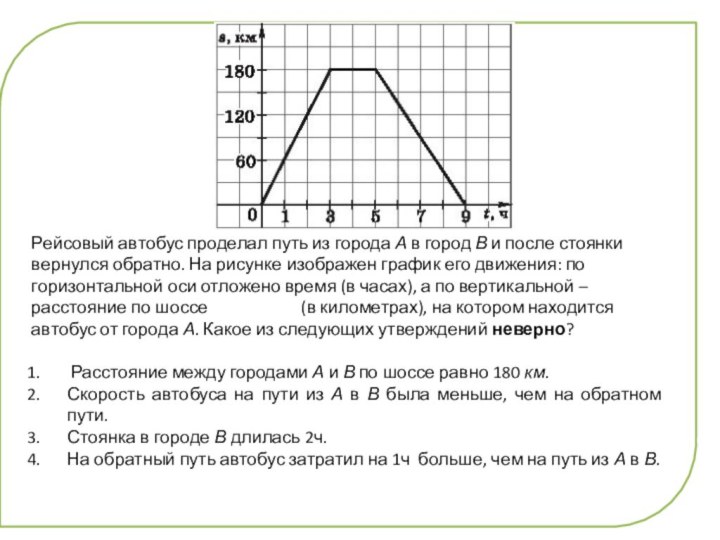
Рейсовый автобус проделал путь из города А в
город В и после стоянки вернулся обратно. На рисунке
изображен график его движения: по горизонтальной оси отложено время (в часах), а по вертикальной – расстояние по шоссе (в километрах), на котором находится автобус от города А. Какое из следующих утверждений неверно?Расстояние между городами А и В по шоссе равно 180 км.
Скорость автобуса на пути из А в В была меньше, чем на обратном пути.
Стоянка в городе В длилась 2ч.
На обратный путь автобус затратил на 1ч больше, чем на путь из А в В.
Слайд 21 1.График функции y = x3 + 1 -
кубическая парабола
2.Функция y = -x2 + 3x
- квадратичная функция3. y = 3 – x2 - линейная функция
4. D(f) функции y = Ѵх - все действительные положительные числа
5. D(f) функции y =1/ (х-2) - все действительные числа
6. График функции y = x2 /4 - парабола
7. График функции у= 3/х - гипербола
8. y = -5x + 4 - убывающая функция;
9. y = x2 -3x - монотонная функция.





























