- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к уроку Возрастание и убывание функции
Содержание
- 2. Изучение нового материала1) Если
- 3. Изучение нового материала2) Если
- 4. Пример Найдите промежутки возрастания (убывания) функции
- 5. Изучение нового материалаЕсли в точке
- 6. Закрепление1. Определить по графику промежутки возрастания функции.
- 7. Закрепление2. Определить по графику промежутки убывания функции.
- 8. Закрепление3. Указать интервалы возрастания функций, графики которых представлены на рисунках
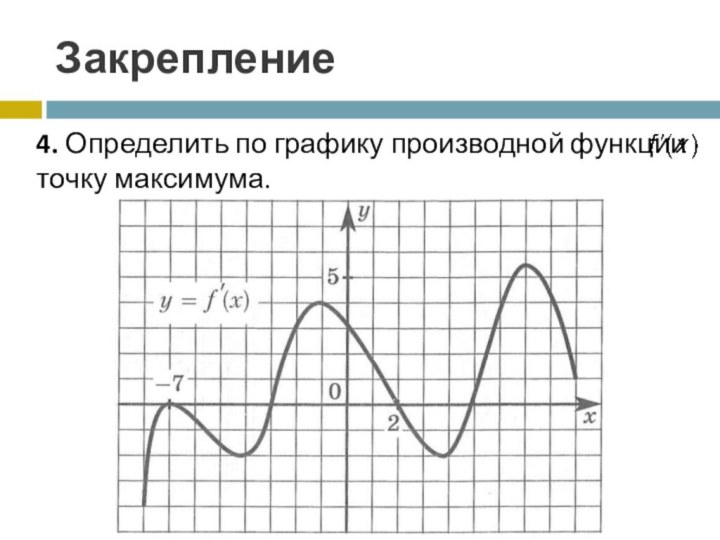
- 9. Закрепление4. Определить по графику производной функции точку максимума.
- 10. Закрепление5. Определить точку минимума функции
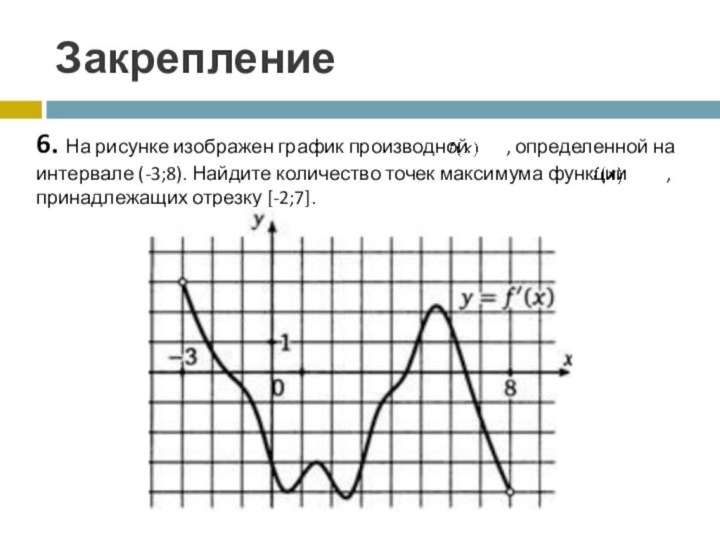
- 11. Закрепление6. На рисунке изображен график производной
- 12. Закрепление7. Найдите точку локального максимума функции
- 13. Закрепление8. Найдите критические точки, промежутки возрастания и
- 14. Скачать презентацию
- 15. Похожие презентации
Изучение нового материала1) Если для каждого x внутри промежутка I, то функция f(x) возрастает на промежутке I.











Слайд 3
Изучение нового материала
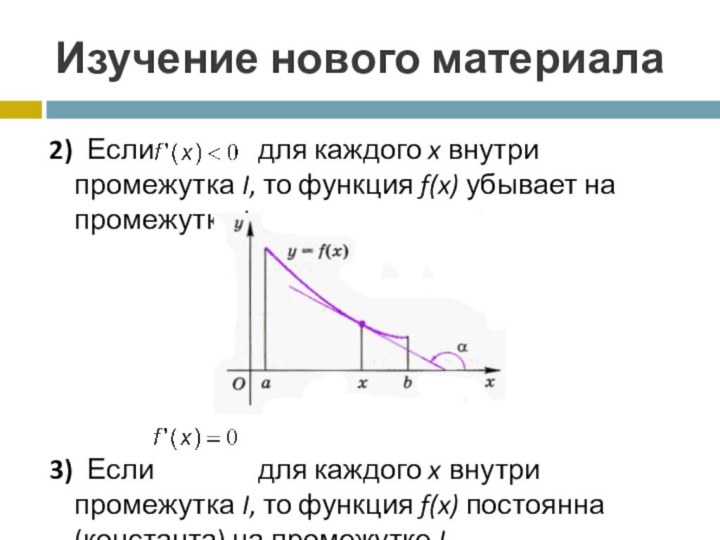
2) Если
для каждого x внутри промежутка I, то
функция f(x) убывает на промежутке I.3) Если для каждого x внутри промежутка I, то функция f(x) постоянна (константа) на промежутке I.
Слайд 5
Изучение нового материала
Если в точке производная
меняет знак с «+» на «-», то
– точка локального максимума (рис. 1).Если в точке производная меняет знак с «-» на «+», то – точка локального минимума (рис. 2).
(Рис. 1).
(Рис. 2).