- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по алгебре Одночлен и его стандартный вид
Содержание
- 2. Цель урока: изучить:понятие одночлена, его стандартного вида;понятие
- 3. План урока. Устная работаОбъяснение нового материала.Решение практических задач.Обучающая самостоятельная работа(тестирование).Подведение итогов урока.
- 4. Ни костяшек. Ни ручек, ни мела –
- 5. Устная работа. Выполняя задания на преобразование выражений,
- 6. Вычислить:2³ · 2 : (2²)³ · 2
- 7. -Когда римляне завоевали греков, развитие математики надолго
- 8. Выражения, которые являются произведениями чисел, переменных и
- 9. Упростим одночлен 2b²(-3)bc² воспользовавшись переместительным и сочетательным
- 10. Числовой множитель одночлена, записанного в стандартном виде,
- 11. Степенью одночлена называют сумму показателей степеней всех
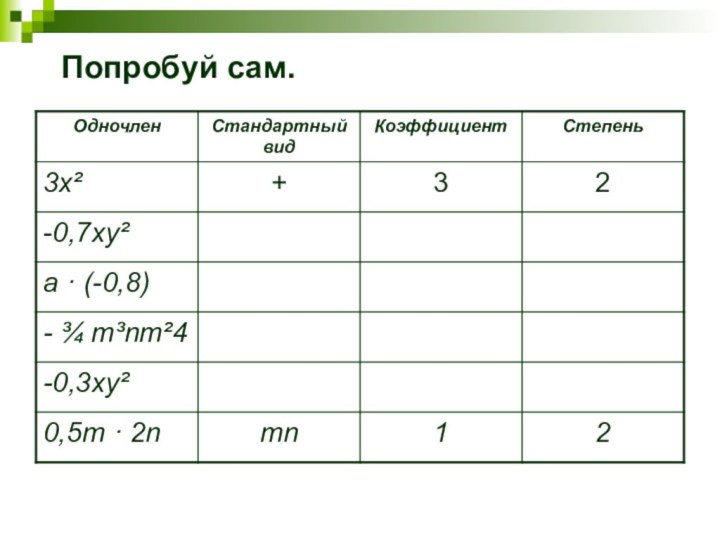
- 12. Попробуй сам.
- 13. Попробуй сам.
- 14. Выполнение упражнений.Решить № 465(д); № 467(а, г).
- 15. Доска бела от мела,Рука устала, затекла спина,Мы
- 16. Выполнить тест.Какое из данных выражений не является
- 17. Выполнить тест.Какое из данных выражений не является
- 18. ИТОГ УРОКА.Что называется одночленом, коэффициентом одночлена, его
- 19. Домашнее задание.Алгебра: Учеб. для 7 кл. общеобразоват.
- 20. Скачать презентацию
- 21. Похожие презентации
Цель урока: изучить:понятие одночлена, его стандартного вида;понятие коэффициента одночлена;понятие степени одночлена; научиться:приведению одночленов к стандартному виду.



















Слайд 2
Цель урока:
изучить:
понятие одночлена, его стандартного вида;
понятие коэффициента
одночлена;
Слайд 3
План урока.
Устная работа
Объяснение нового материала.
Решение практических задач.
Обучающая самостоятельная
работа(тестирование).
Подведение итогов урока.
Слайд 4
Ни костяшек. Ни ручек, ни мела –
Устный
счет. Мы творим это дело
Только силой ума и души!
Числа
сходятся где – то во тьме,И глаза начинают светиться!
И кругом только умные лица.
Устный счет! Мы считаем в уме.
Слайд 5
Устная работа.
Выполняя задания на преобразование выражений, содержащих степени,
ученик допустил следующие ошибки:
Какие определения, свойства, правила не знает
ученик?3· 3· 3· 3· 3 = 5³
(-2)² = -2 · 2 = -4
8¹ = 1
3² · 3¹º = 3²º
5² · 5³ = 10
2² + 2 = 2
3¹º : 3² = 3
(2а) = 2а
(х²)³ = х
(а³)(а²) = (а²) = а¹
Слайд 7 -Когда римляне завоевали греков, развитие математики надолго остановилось.
На целую тысячу лет ! Возродили математику арабы. Выдающийся
арабский поэт-математик Омар Хайям писал когда-то:… Мне мудрость не чужда была земная,
Разгадки тайн ища, не ведал сна я.
За семьдесят перевалило мне,
Что ж я узнал? –
Что ничего не знаю.
Слайд 8 Выражения, которые являются произведениями чисел, переменных и их
степеней, называются одночленами.
Например:
5а²х, 2b³(-3)bc², xy², a¹².
Одночленами считают также числа, переменные и их степени.
Например: -7, 2³, x, x³ .
Является ли одночленом выражение:
а) 4,3х²у; б) -0,55ху³; в) а(- 4);
г) х³ + х; д) у²²у; е) 6?
Слайд 9 Упростим одночлен 2b²(-3)bc² воспользовавшись переместительным и сочетательным свойствами
умножения:
2b²(-3)bc² = 2(-3)b²bc² = -6b³c².
Одночлен, представленный в виде
произведения числового множителя, стоящего на первом месте, и степеней различных переменных, называют одночленом стандартного вида.К стандартному виду можно привести любой одночлен.
Записан ли в стандартном виде одночлен:
а) 5ав; б) -4хух; в) 0,5х · 2у;
г) –вас; д) 9р²р³; е) -а¹º?
Слайд 10 Числовой множитель одночлена, записанного в стандартном виде, называют
коэффициентом одночлена.
Например, -5х²у
-5 коэффициент одночлена
Коэффициенты одночленов
а² и - ab считают равными соответственно 1 и -1.Слайд 11 Степенью одночлена называют сумму показателей степеней всех входящих
в него переменных. Если одночлен не содержит переменных (т.
е. является числом), то его степень считают равной нулю.
Слайд 15
Доска бела от мела,
Рука устала, затекла спина,
Мы друг
на друга смотрим очумело,
А всё-таки задача решена!
Додумались! Добились! «Раскололи»!
Намаялись,
однако же смогли!Забыли о кино и о футболе
Звонку не рады – до чего дошли.
Слайд 16
Выполнить тест.
Какое из данных выражений не является одночленом?
1) 8ху²; 2) 3;
3) 2ав; 4) х² + х.2. Привести одночлен 8х³ · у · х · у² к стандартному виду:
1) 8ху²; 2) 8ху; 3) 8ху²; 4) 8ху.
3. Найдите значение одночлена -32х²у при х = ½, у = -1
1) ⅛; 2) - ⅛; 3) 8; 4) – 8.
4. Степень одночлена 8ав³с² равна:
1) 5; 2) 6; 3) 7; 4) 8.
5. Какай из одночленов имеет стандартный вид 8ав?
1) -4а²в · 4ав; 2) -4а²в · (-2ав);
3) -4а²в · (- 2а); 4) -4а²в · 4а²в.
Слайд 17
Выполнить тест.
Какое из данных выражений не является одночленом?
1) 8ху²; 2) 3;
3) 2ав; 4) х² + х.2. Привести одночлен 8х³ · у · х · у² к стандартному виду:
1) 8ху²; 2) 8ху; 3) 8ху²; 4) 8ху.
3. Найдите значение одночлена -32х²у при х = ½, у = -1
1) ⅛; 2) - ⅛; 3) 8; 4) – 8.
4. Степень одночлена 8ав³с² равна:
1) 5; 2) 6; 3) 7; 4) 8.
5. Какай из одночленов имеет стандартный вид 8ав?
1) -4а²в · 4ав; 2) -4а²в · (-2ав);
3) -4а²в · (- 2а); 4) -4а²в · 4а²в.
Слайд 18
ИТОГ УРОКА.
Что называется одночленом, коэффициентом одночлена, его степенью?
Приведите
пример одночлена стандартного вида и назовите его коэффициент. Чему
равна степень данного одночлена?
Слайд 19
Домашнее задание.
Алгебра: Учеб. для 7 кл. общеобразоват. учреждений
/ Ю. Н. Макарычев, Н.
Г. Миндюк, К. И. Нешков, С. Б. Суворова; под ред. С. А. Теляковского.П. 19, стр. 83 – 85, № 466, 473.